Bộ ba Pitago và những thông tin liên quan mới nhất về nó

Bộ ba Pitago là gì?

Bộ ba (PT) Pitago có thể được định nghĩa là một bộ ba số nguyên dương thỏa mãn hoàn toàn định lý Pitago: a ²  + b ² = c ² .

Những bộ số này thường là độ dài ba cạnh của một tam giác vuông. Bộ ba Pitago được biểu diễn là: (a, b, c), trong đó, a = một chân; b = chân khác; và c = cạnh huyền.

Có hai loại bộ ba Pitago:

• Bộ ba Pythagore nguyên thủy
• Bộ ba Pythagore không nguyên thủy

Bộ ba Pythagore nguyên thủy

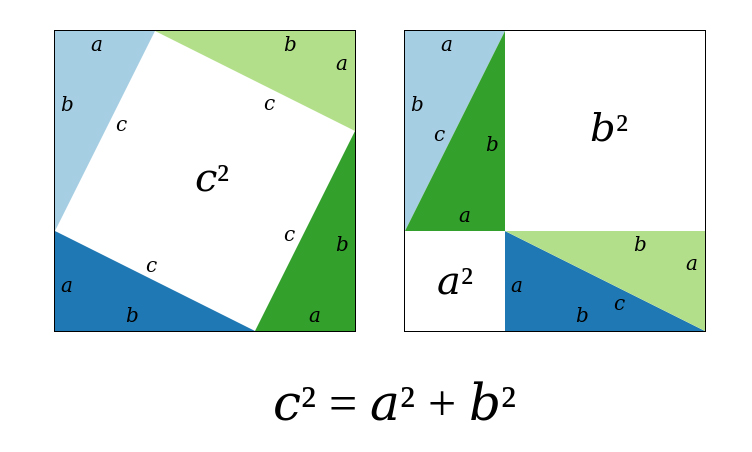
Bộ ba Pitago nguyên thủy là một tập hợp rút gọn các giá trị dương của a, b và c với nhân tử chung khác 1 . Loại bộ ba này luôn bao gồm một số chẵn và hai số lẻ.

Ví dụ , (3, 4, 5) và (5, 12, 13) là các ví dụ về bộ ba Pythagore nguyên thủy bởi vì, mỗi tập hợp có nhân tử chung là 1 và cũng thỏa mãn

Định lý Pitago: a ²  + b ² = c ² .

• (3, 4, 5) → GCF = 1

a ²  + b ² = c ²

3 ²  + 4 ² = 5 ²

9 + 16 = 25

25 = 25

• (5, 12, 13) → GCF = 1

a ²  + b ² = c ²

5 ²  + 12 ² = 13 ²

25 + 144 = 169

169 = 169

Bộ ba Pythagore không nguyên thủy

Bộ ba Pythagore không nguyên thủy, còn được gọi là bộ ba Pythagore bắt buộc là tập hợp các giá trị dương của a, b và c với nhân tử chung lớn hơn 1 . Nói cách khác, bộ ba giá trị dương trong bộ ba Pitago không nguyên thủy đều là số chẵn.

Ví dụ về bộ ba Pythagore không nguyên thủy bao gồm : (6,8,10), (32,60,68), (16, 30, 34), v.v.

• (6,8,10) → GCF của 6, 8 và 10 = 2.

a ²  + b ² = c ²

6 ²  + 8 ² = 10 ²

36 + 64 = 100

• = 100
• (32,60,68) → GCF của 32, 60 và 68 = 4

a ²  + b ² = c ²

32 ²  + 60 ² = 68 ²

1,024 + 3,600 = 4,624

4,624 = 4,624

Các ví dụ khác về bộ ba số Pitago thường được sử dụng bao gồm: (3, 4, 5), (5, 12, 13), (8, 15, 17), (7, 24, 25), (20, 21, 29), ( 12, 35, 37), (9, 40, 41), (28, 45, 53), (11, 60, 61), (16, 63, 65), (33, 56, 65), (48, 55, 73), v.v.

Tính chất của bộ ba Pitago

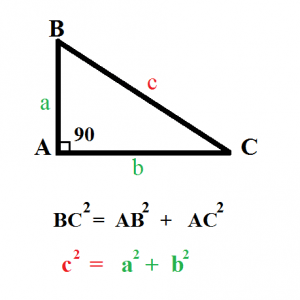
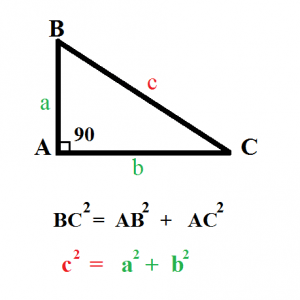
Từ hình ảnh minh họa trên về các loại bộ ba Pitago, chúng tôi đưa ra kết luận sau về bộ ba số Pitago :

• Một bộ ba Pitago không thể chỉ bao gồm các số lẻ.
• Tương tự, một bộ ba một bộ ba Pitago không bao giờ có thể chứa một số lẻ và hai số lẻ.
• Nếu (a, b, c) là bộ ba Pitago thì a hoặc b là chân ngắn hoặc chân dài của tam giác và c là cạnh huyền.

Công thức bộ ba Pythagore

Cả bộ ba Pythagore nguyên thủy và bộ ba Pythagore không nguyên thủy đều có thể được tạo ra bằng công thức bộ ba Pitago.

Công thức bộ ba Pitago được đưa ra là:

(a, b, c) = [(m ²  – n ² ); (2mn); (m ²  + n ² )]

Trong đó, m và n là hai số nguyên dương và m> n

LƯU Ý : Nếu biết một thành viên của bộ ba, các thành viên còn lại có thể được lấy bằng cách sử dụng công thức: (a, b, c) = [(m ² -1), (2m), (m ² +1)].

ví dụ 1

Bộ ba Pitago của hai số dương, 1 và 2 là gì?

Giải pháp

Cho công thức bộ ba Pitago: (a, b, c) = (m ²  – n ² ; 2mn; m ²  + n ² ), trong đó; m> n.

Vì vậy, cho m = 2 và n = 1.

Thay các giá trị của m và n vào công thức.

⇒ a = 2 ²  – 1 ²  = 4 – 1 = 3

a = 3

⇒ b = 2 × 2 × 1 = 4

b = 4

⇒ c = 2 ²  + 1 ²  = 4 + 1 = 5

c = 5

Áp dụng định lý Pitago để xác minh rằng (3,4,5) thực sự là một bộ ba Pitago

⇒ a ²  + b ² = c ²

⇒ 3 ²  + 4 ² = 5 ²

⇒ 9 + 16 = 25

⇒ 25 = 25.

Vâng, nó đã hoạt động! Do đó, (3,4,5) là một bộ ba Pitago

Ví dụ 2

Tạo bộ ba số Pitago từ hai số nguyên 5 và 3.

Giải pháp

Vì m phải lớn hơn n (m> n) nên m = 5 và n = 2.

a = m ²  – n ²

⇒a = (5) ² – (3) ² = 25−9

= 16

⇒ b = 2mn = 2 x 5 x 3

= 30

⇒ c = m ²  + n ² = 3 ² + 5 ²
= 9 + 25
= 34

Do đó, (a, b, c) = (16, 30, 34).

Xác minh câu trả lời.

⇒ a ²  + b ² = c ²

⇒ 16 ²  + 30 ² = 34 ²

⇒ 256 + 900 = 1,156

1,156 = 1,156 (Đúng)

Do đó, (16, 30, 34) thực sự là một bộ ba của Pitago.

Ví dụ 3

Kiểm tra xem (17, 59, 65) có phải là bộ ba Pitago hay không.

Giải pháp

Cho, a = 17, b = 59, c = 65.

Kiểm tra xem, a ²  + b ² = c ² .

a ²  + b ² ⇒ 17 ²  + 59 ²

⇒ 289 + 3481 = 3770

c ² = 65 ²

= 4225

Vì, 3770 ≠ 4225, thì (17, 59, 65) không phải là một bộ ba Pitago.

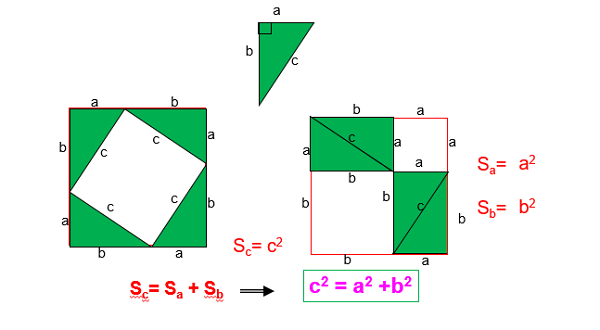
Ví dụ 4

Tìm giá trị có thể có của ‘a’ trong bộ ba Pitago sau: (a, 35, 37).

Giải pháp

Áp dụng phương trình Pitago a ²  + b ² = c ² .

a ²  + 35 ² = 37 ² .

a ² = 37 ² −35 ² = 144. Trong khi đó, bạn sẽ không gặp phải khó khăn gì.

√a ² = √144

a = 12.

Ví dụ 5

Tìm bộ ba Pitago của một đường tròn bên phải có cạnh huyền là 17 cm.

Giải pháp

(a, b, c) = [(m ² -1), (2m), (m ² +1)]

c = 17 = m ² +1

17 – 1 = m ²

m ² = 16

m = 4.

Vì thế,

b = 2m = 2 x 4

= 8

a = m ² – 1

= 4 ² – 1

= 15

Ví dụ 6

Cạnh nhỏ nhất của tam giác vuông là 20mm. Tìm tam giác Pitago của tam giác.

Giải pháp

(a, b, c) = [(2m), (m ² -1), (m ² +1)]

20 = a = 2m

2m = 20

m = 10

Thay m = 10 vào phương trình.

b = m ² – 1

= 10 ² – 1 = 100 – 1

b = 99

c = m ² +1

= 10 ² + 1

= 100 + 1 = 101

PT = (20, 99, 101)

Ví dụ 7

Tạo bộ ba số Pitago từ hai số nguyên 3 và 10.

Giải pháp

(a, b, c) = (m ²  – n ² ; 2mn; m ²  + n ² ).

a = m ²  – n ²

= 10 ² – 3 ² = 100 – 9

= 91.

b = 2mn = 2 x 10 x 3

= 60

c = m ²  + n ²

= 10 ² + 3 ² = 100 + 9

= 109.

PT = (91, 60.109)

Xác minh câu trả lời.

a ²  + b ² = c ² .

91 ²  + 60 ² = 109 ² .

8.281+ 3.600 = 11.881

11.881 = 11.881 (Đúng)

Ví dụ 8

Kiểm tra xem tập hợp (24, 7, 25) có phải là bộ ba số Pitago hay không .

Giải pháp

Cho a = 24, b = 7 và c = 25.

Theo định lý Pitago: a ²  + b ² = c ²

7 ²  + 24 ² = 625

49 + 576 = 625 (Đúng)

Do đó, (24, 7, 25) là một bộ ba của Pitago.

Xem thêm:

Tam giác 45 ° -45 ° -90 ° là gì? Hướng dẫn cách giải đơn giản nhất

Bất đẳng thức tam giác là gì và những ví dụ điển hình nhất

Ví dụ 9

Tìm tam giác Pitago của một tam giác vuông có một cạnh là 18 thước.

Giải pháp

Cho công thức: (a, b, c) = [(m ² -1), (2m), (m ² +1)].

Cho a hoặc b = 18 thước.

2m = 18

m = 9.

Thay m = 9 vào công thức.

c = m ² + 1

= 9 ² + 1 = 81

b hoặc a = m ² -1 = 9 ² -1

= 80

Do đó, các trường hợp sinh ba có thể là; (80, 18, 81) hoặc (18, 80, 81).