Các loại hình tam giác và tất tần tật thông tin về nó

Trong Hình học, hình tam giác là hình dạng quan trọng nhất , được định nghĩa là một sơ đồ hai chiều khép kín chứa 3 cạnh, 3 góc và 3 đỉnh. Nói một cách dễ hiểu, tam giác là một đa giác có 3 cạnh. Từ tam giác được lấy từ từ tiếng Latinh ‘triangulus’, có nghĩa là ba góc.

Trong thời cổ đại, các nhà thiên văn học đã tạo ra một phương pháp gọi là phương pháp tam giác để xác định khoảng cách của các ngôi sao ở xa. Họ đo khoảng cách từ hai địa điểm khác nhau, sau đó đo góc tạo bởi dịch chuyển hoặc thị sai, được hình thành bởi chuyển động của người quan sát giữa hai địa điểm. Sau đó, họ sử dụng luật sines để tính khoảng cách cần thiết.

Kim tự tháp Ai Cập được tạo ra vào khoảng năm 2900 trước Công nguyên. Hình dạng của nó thực sự là kim tự tháp 3D, có các mặt hình tam giác. Đây là mô hình được thiết kế hoàn hảo với độ dài và góc ở tất cả các mặt đều giống nhau. Miletus (624 TCN – 547 TCN), một nhà toán học Hy Lạp, đã tiếp nhận hình học từ Ai Cập và mang đến Hy Lạp.

Aristarchus (310 TCN – 250 TCN), một nhà toán học người Hy Lạp, đã sử dụng phương pháp trên để tìm khoảng cách giữa Trái đất và Mặt trăng. Eratosthenes (276 TCN – 195 TCN), một lần nữa, sử dụng cùng một phương pháp để xác định khoảng cách xung quanh bề mặt Trái đất (gọi là chu vi).

Trong bài này, chúng ta sẽ thảo luận về ý nghĩa của một hình tam giác , các loại hình tam giác khác nhau và các tính chất của chúng cũng như ứng dụng thực tế của hình tam giác.

Tam giác là gì?

Hình tam giác là một hình khép kín hai chiều có 3 cạnh. Đó là một đa giác có ba góc, ba đỉnh và ba góc ghép với nhau tạo thành một sơ đồ khép kín. Ta dùng kí hiệu ∆ để biểu thị một tam giác.

Hình A và B là hình tam giác.

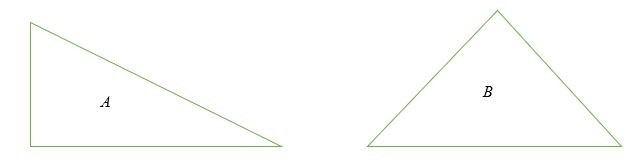
Các loại hình tam giác khác nhau

Các loại hình tam giác được phân loại dựa trên cơ sở:

• Chiều dài các cạnh của chúng
• Góc nội thất

Phân loại tam giác theo số đo các góc trong

Theo số đo của các góc bên trong, hình tam giác có thể được phân thành ba loại:

1. Góc cạnh
2. Góc cạnh
3. Góc phải

Tam giác nhọn

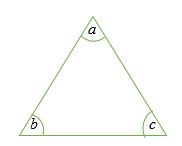
Tam giác góc nhọn là tam giác trong đó cả ba góc trong đều nhỏ hơn 90 độ.

Mỗi góc a, b và c nhỏ hơn 90 độ.

Hình tam giác

Tam giác tù là tam giác có một trong các góc bên trong lớn hơn 90 độ.

Góc a là góc tù trong khi góc b và c là góc nhọn.

Tam giác phải

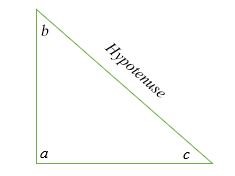
Tam giác vuông là tam giác có một trong các góc chính xác là 90 độ. Cạnh huyền là cạnh của một tam giác vuông với độ dài dài nhất.

Trong hình minh họa trên, góc a = 90 độ trong khi góc b và c là góc nhọn.

Phân loại tam giác theo độ dài các cạnh của chúng

Hình tam giác có thể được phân thành 3 loại dựa trên độ dài các cạnh của chúng:

1. Scalene
2. Isosceles
3. Ngang bằng

Tam giác cân

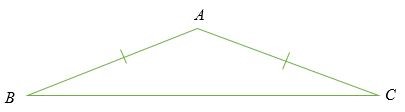
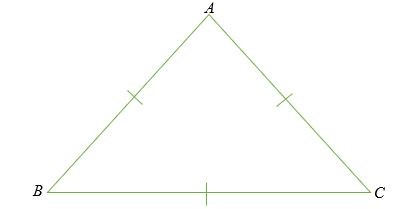
Tam giác cân là tam giác có hai cạnh và hai góc bằng nhau. Độ dài bằng nhau của một tam giác được thể hiện bằng cách tạo một cung ở mỗi cạnh.

Trong sơ đồ trên , độ dài cạnh AB = AC và ∠ ABC = ∠ ACB.

Tam giác đều

Một tam giác đều có cả ba cạnh bằng nhau và cả ba góc trong cũng bằng nhau. Trong trường hợp này, mỗi góc trong của một tam giác đều là 60 độ. Một tam giác đều đôi khi được gọi là tam giác đồng dạng vì cả ba góc đều bằng nhau.

Trong một tam giác đều, các cạnh AB = BC = AC và ∠ ABC = ∠ ACB = ∠ BAC

Lưu ý rằng, các góc của một tam giác đều không phụ thuộc vào độ dài các cạnh.

Tam giác Scalene

Tam giác vô hướng là tam giác trong đó tất cả các cạnh có số đo khác nhau và tất cả các góc bên trong cũng khác nhau.

Các thuộc tính của Tam giác

Các tính chất của hình tam giác có một công dụng rộng rãi. Nhiều nhà toán học đã sử dụng nó trong việc giải quyết các vấn đề của họ. Hình học Euclide và lượng giác sử dụng rất nhiều các tính chất của tam giác.

Dưới đây là một số tính chất cơ bản của tam giác:

• Một tam giác là một đa giác 2-D
• Một tam giác có 3 cạnh, 3 góc và 3 đỉnh.
• Tổng độ dài hai cạnh bất kỳ của tam giác lớn hơn độ dài cạnh còn lại.
• Tổng độ dài của ba cạnh là chu vi của một hình tam giác.
• Diện tích của một tam giác bằng tích của đáy và chiều cao.

Các ví dụ đã làm về các loại hình tam giác khác nhau

ví dụ 1

Tìm giá trị của góc x trong tam giác dưới đây.

Giải pháp

Đây là tam giác cân trong đó hai cạnh bằng nhau và hai góc cũng bằng nhau. Vì thế,

x = (180 ° – 70 °) / 2

x = 110 ° / 2

= 55 °

Ví dụ 2

Tìm góc y trong tam giác vuông dưới đây.

Giải pháp

Một góc của tam giác vuông bằng 90 °. Vì vậy, chúng tôi;

y + 50 + 90 = 180

y = (180 – 140) °

y = 40 °

Ví dụ 3

Phân loại tam giác sau.

Giải pháp

Đây là một tam giác vô hướng vì tất cả các cạnh và góc có số đo khác nhau. Tương tự, tam giác cũng có thể được xếp vào dạng tam giác tù vì một góc là góc tù.

Ví dụ 4

Phân loại tam giác được hiển thị bên dưới.

Giải pháp

Đây là một tam giác cân. Hai cạnh bên bằng nhau và hai góc có số đo bằng nhau.

Xem thêm:

Bộ ba Pitago và những thông tin liên quan mới nhất về nó

Các góc của một tam giác và những giải thích chi tiết nhất

Các ứng dụng của hình tam giác

Hãy cùng khám phá một số ứng dụng trong thực tế của hình tam giác:

• Biển báo Giao thông: Hầu hết các biển báo giao thông được hiển thị trên các cấu trúc hình tam giác.
• Kim tự tháp Ai Cập: Kim tự tháp là những di tích cổ đại do người Ai Cập xây dựng. Kim tự tháp có dạng hình tam giác.
• Kèo: Kèo của mái nhà hoặc cầu được chế tạo theo hình tam giác vì hình tam giác được coi là hình mạnh nhất.
• Tam giác quỷ Bermuda: Tam giác quỷ Bermuda là một khu vực hình tam giác ở Đại Tây Dương, nơi người ta tin rằng bất kỳ con tàu hoặc máy bay nào đi qua điểm này đều bị nuốt chửng. 50 tàu và 20 tàu hàng không được cho là đã biến mất một cách bí ẩn tại Tam giác quỷ Bermuda.
• Hệ thống định vị toàn cầu (GPS) hoạt động dựa trên thuật toán tam giác để xác định kinh độ và vĩ độ của một đối tượng.
• Một cái thang dựa vào tường tạo thành hình tam giác.
• Tháp Eiffel có hình tam giác.
• Khái niệm tam giác được sử dụng để tính chiều cao hoặc độ cao của các vật thể cao như cột cờ, núi, tòa nhà, v.v.
• Bánh mì sandwich và lát bánh pizza có hình tam giác.