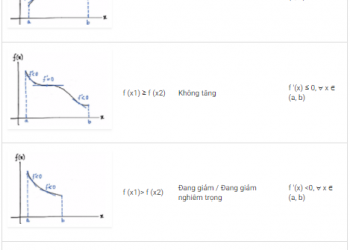
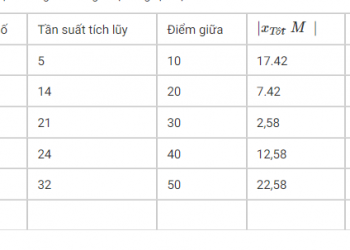
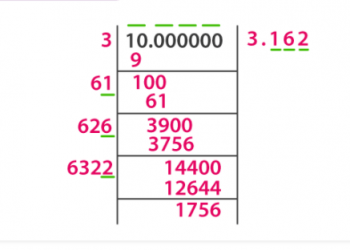
Tìm căn bậc hai của số bằng tay
Trước khi tiếp tục, điều rất quan trọng là phải hiểu rõ ràng các số bình phương . Phép nhân là quá trình tính toán một số với một số khác. Điều đó có nghĩa là gì khi ai đó nói bình phương của một số? Bình phương một số có nghĩa là nhân nó với chính nó.
Ví dụ 1:
- 2 nhân với 2 được thương là 4
- Có một cách ngắn hơn để viết 2 * 2. Nó được viết là 2 2
- Nó còn được gọi là 2 bình phương hoặc 2 lũy thừa 2
Ví dụ 2:
- 5 nhân với 5 được 25
- Có một cách ngắn hơn để viết 5 * 5. Nó được viết là 5 2
- Nó còn được gọi là 5 bình phương hoặc 5 lũy thừa 2
Căn bậc hai của một số là một số khác khi nhân với chính nó sẽ trả lại số ban đầu. Các phương pháp tìm căn bậc hai: 1. Phương pháp trừ nhiều lần 2. Phương pháp nhân thừa số nguyên tố 3. Phương pháp chia dài. Có một số quy tắc căn bậc hai cần phải được tuân theo trong khi tính căn bậc hai . Ký hiệu được sử dụng để biểu thị gốc của một số được gọi là căn. Mỗi căn đều có 3 phần: ký hiệu căn, chỉ số, và radicand.
Các ví dụ
Ví dụ 1:
- Căn bậc hai của 36 là 6
- Được viết là = 6 vì 6 * 6 = 6 2 = 3636–√
Ví dụ 2:
- Căn bậc hai của 25 là 5
- Được viết là = 5 vì 5 * 5 = 5 2 = 2525–√
Làm thế nào để giải quyết các phương trình căn bậc hai?
Chúng ta hãy xem xét một phương trình cấp tiến, có giá trị căn bậc hai trong nó.
√ (x + 1) = 9
Như chúng ta có thể thấy trong phương trình trên, chúng ta đã sử dụng căn mà theo đó một biến x được đề cập. Vì chỉ có một biến, do đó chúng ta sẽ nhận được nghiệm cho x. Hãy để chúng tôi giải quyết phương trình này bây giờ.
Để loại bỏ hình vuông, chúng ta cần bình phương các phương trình ở cả hai bên, tức là, LHS và RHS
Do đó, chúng tôi nhận được;
[√ (x + 1)] 2 = [9] 2
x + 1 = 81
x = 81-1
x = 80.
Xem thêm: