Cách tính căn bậc hai của một số nhanh gọn đơn giản nhất

Căn bậc hai là một phép toán nghịch đảo của bình phương một số .

Căn bậc hai của một số x được biểu thị bằng dấu căn √x hoặc x ^1/2 . Căn bậc hai của một số x sao cho một số y là bình phương của x, viết đơn giản là y ²  = x.

Ví dụ, căn bậc hai của 25 được biểu diễn là: √25 = 5. Một số có căn bậc hai được tính được gọi là radicand. Trong biểu thức này, √25 = 5 số 25 là bán kính.

Đôi khi, bạn nhận được các biểu thức phức tạp với nhiều gốc và được yêu cầu đơn giản hóa điều đó.

Có nhiều kỹ thuật để làm điều đó, tùy thuộc vào số lượng gốc và các giá trị dưới mỗi gốc. Chúng ta sẽ xem từng cái một.

Làm thế nào để Đơn giản hóa Rễ Vuông?

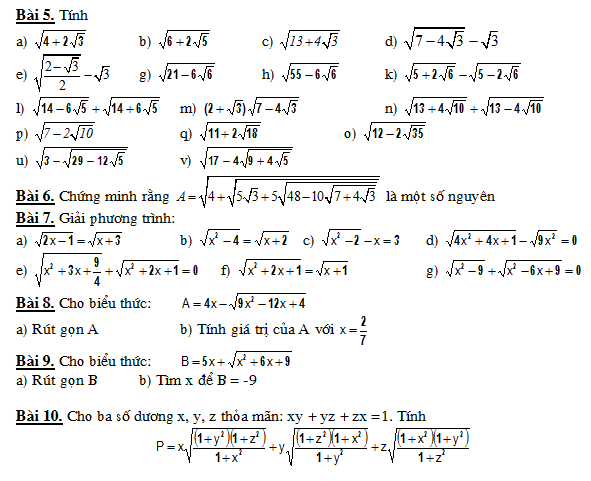
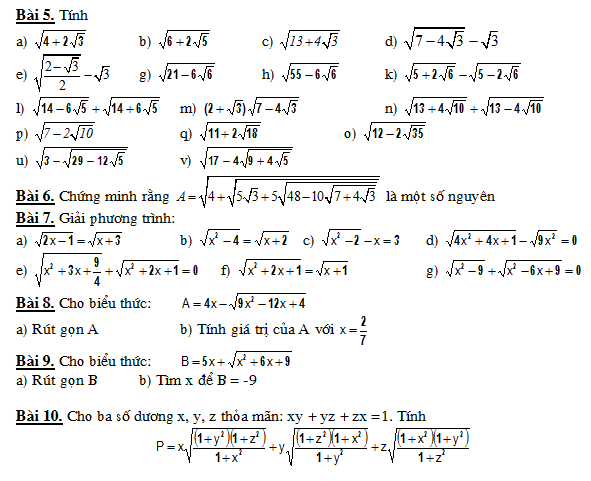
Để đơn giản hóa một biểu thức có chứa căn bậc hai, chúng ta tìm các thừa số của số và nhóm chúng thành từng cặp.

Ví dụ , một số 16 có 4 bản sao của thừa số, vì vậy chúng ta lấy một số hai từ mỗi cặp và đặt nó ở phía trước của căn, cuối cùng bị bỏ đi tức là √16 = √ (2 x 2 x 2 x 2) = 4.

Việc đơn giản hóa căn bậc hai của một số đòi hỏi một số phương pháp. Bài viết này phác thảo một số phương pháp này.

Đơn giản hóa khi các bộ đổi tên khác nhau

Bạn chỉ có thể cộng hoặc trừ các căn bậc hai nếu các giá trị dưới dấu căn bằng nhau. Sau đó, chỉ cần cộng hoặc trừ các hệ số (các số đứng trước dấu căn) và giữ nguyên số ban đầu trong dấu căn.

ví dụ 1

Thực hiện các thao tác sau

1. 2√3 + 3√3 = (2 +3) √3

= 5√3

1. 4√6 – 2√6 = (4 – 2) √6

= 2√6

• 5√2 + √2 = (5+ 1) √2

= 6√2

Xem thêm:

Các bộ đếm có phân số nhanh gọn nhất bạn cần nhớ

Các loại số trong toán học cho người chưa rõ

Đơn giản hóa dưới một dấu căn duy nhất

Bạn có thể đơn giản hóa căn bậc hai khi các số nguyên dưới một dấu đơn bằng cách cộng, trừ và nhân các số nguyên dưới dấu.

Ví dụ 2

Đơn giản hóa các biểu thức sau:

• √ (5 x20)

= √100

= 10

• √ (30 + 6)

= √36

= 6

• √ (30 – 5)

= √25

= 5

• √ (3 + 8)

= √11

Đơn giản hóa khi các giá trị Radical khác nhau

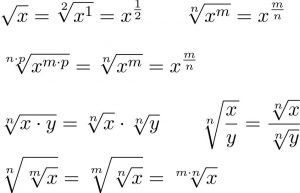
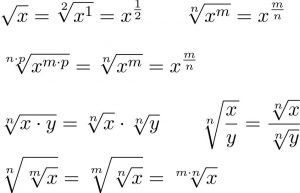
Khi các căn không giống nhau, hãy đơn giản hóa bình phương của một số, bằng cách cộng hoặc trừ các căn bậc hai khác nhau.

Ví dụ 3

Thực hiện các thao tác sau:

• √50 + 3√2

= √ (25 x 2) + 3√2

= 5√2 + 3√2

= 8√2

• √300 + √12

= √ (100 x 3) + √ (4 x 3)

= 10√3 + 2√3

= 12√3

Đơn giản hóa bằng cách nhân các rễ không âm

Ví dụ 4

Nhân:

• √2 x √8 = √16

= 4

• √x ³+ √x ⁵

= √x ⁸ = x ⁴

 Ví dụ 5

Tìm giá trị của số n nếu căn bậc hai của tổng của số với 12 là 5.

Giải pháp

Viết biểu thức của bài toán này, căn bậc hai của tổng n và 12 là 5
√ (n + 12) = căn bậc hai của tổng.

√ (n + 12) = 5
Phương trình cần giải bây giờ là:
√ (n + 12) = 5
Mỗi
vế của phương trình là bình phương: [√ (n + 12)] ² = 5²
[√ (n + 12) ] x [√ (n + 12)] = 25
√ [(n + 12) x √ (n + 12)] = 25
√ (n + 12) ² = 25
n + 12 = 25
Trừ 12 cho cả hai vế của biểu thức
n + 12 – 12 = 25 – 12
n + 0 = 25 – 12
n = 13

Ví dụ 6

Đơn giản hóa

1. √4.500
2. √72

Giải pháp

Đối số 4500 có các thừa số 5, 9 và 100. Bây giờ có thể tính căn bậc hai của nó. Tính căn bậc hai của số bình phương hoàn hảo

√4500 = √ (5 x 9 x 100)

= 30√5

2.

Số 72 bằng 2 x 36, và vì 36 là một hình vuông hoàn hảo, hãy tính căn bậc hai của nó.

√ (2 x 36)

= 6√2

Câu hỏi thực hành

1. Đơn giản hóa các biểu thức sau:

a) √5x ²

b) √18a

c) √12x ²y

d) √5y ³

e) √ x ⁷y ²

2. Đánh giá biểu thức cấp tiến dưới đây.

a) 2 + 9 –√15−2

b) 3 x 4 + √169

c) √25 x √16 + √36

d) √81 x 12 + 12

e) √36 + √47 – √16

f) 6 + √36 + 25−2

g) 4 (5) + √9 – 2

h) 15 + √16 + 5

i) 3 (2) + √25 + 10

j) 4 (7) + √49 – 12

k) 2 (4) + √9 – 8

l) 3 (7) + √25 + 21

m) 8 (3) – √27

1. Tính diện tích tam giác vuông có cạnh huyền là chiều dài 100 cm và chiều rộng 6 cm.
2. Ahmed và Tom gặp nhau trong một cuộc họp. Đúng 4 giờ chiều, họ chia tay nhau, Tom đi về phía nam với vận tốc 60 dặm / giờ và Ahmed di chuyển về phía đông với vận tốc 30 dặm / giờ. Tom đã cách Ahmed bao xa lúc 4h30 chiều.
3. Tính chiều dài của hình lập phương có diện tích là x cm ² .
4. Tính đường kính của hình tròn có diện tích A = 300 cm².
5. Vườn trường hình vuông có chiều dài 11 m. Nếu mở rộng mỗi cạnh của khu vườn thêm 5 m. Làm thế nào để diện tích của khu vườn được tăng lên?
6. Một tấm chiếu hình chữ nhật có chiều dài 4 mét và chiều rộng √ (x + 2) mét. Tính giá trị của x nếu chu vi là 24 mét.
7. Mỗi cạnh của hình lập phương là 5 mét. Một con nhện nối từ đỉnh của góc khối lập phương đến góc dưới cùng đối diện. Tính tổng chiều dài của mạng nhện.
8. Khu vườn hình vuông có diện tích 144 m ² . Chiều dài mỗi cạnh của khu vườn là bao nhiêu?
9. Một sân chơi hình vuông lớn sẽ được xây dựng trong một thành phố. Nếu diện tích của sân chơi là 400 và sẽ được chia thành bốn khu vực bằng nhau cho các hoạt động thể thao khác nhau. Có bao nhiêu khu vực có thể được đặt trong một hàng của sân chơi mà không vượt qua nó?
11. Một con diều được buộc chặt trên mặt đất bằng một sợi dây. Gió thổi sao cho dây căng và diều được định vị trực tiếp trên cột cờ 30 ft. Tìm chiều cao của cột cờ nếu chiều dài của sợi dây dài 110 ft.