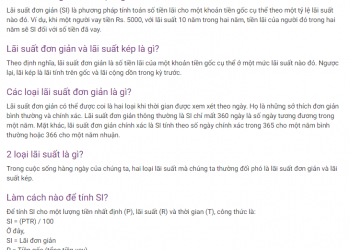
0 ≤ P (E) ≤ 1
Công thức xác suất: Nếu một sự kiện E xảy ra, thì xác suất thực nghiệm của một sự kiện sẽ xảy ra là:
P (E) = Số thử nghiệm trong đó Sự kiện đã xảy ra / Tổng số thử nghiệm
Xác suất lý thuyết của một sự kiện E, P (E), được định nghĩa là:
P (E) = (Số kết quả thuận lợi cho E) / (Số tất cả các kết quả có thể có của thử nghiệm)
Sự kiện không thể xảy ra : Xác suất của một sự kiện / sự kiện không thể xảy ra là 0. Sự kiện như vậy được gọi là sự kiện không thể xảy ra.
Sự kiện chắc chắn: Xác suất của một sự kiện chắc chắn xảy ra là 1. Sự kiện như vậy được gọi là sự kiện chắc chắn hoặc một sự kiện nhất định.
Câu hỏi & câu trả lời về xác suất
1. Hai đồng xu được tung 500 lần, và chúng tôi nhận được:
Hai đầu: 105 lần
Một đầu: 275 lần
Không có đầu: 120 lần
Tìm xác suất xảy ra của mỗi biến cố.
Lời giải: Giả sử biến cố nhận được hai đầu, một đầu và không đầu lần lượt là E 1 , E 2 và E 3 .
P (E 1 ) = 105/500 = 0,21
P (E 2 ) = 275/500 = 0,55
P (E 3 ) = 120/500 = 0,24
Tổng xác suất của tất cả các sự kiện cơ bản của một thí nghiệm ngẫu nhiên là 1.
P (E 1 ) + P (E 2 ) + P (E 3 ) = 0,21 + 0,55 + 0,24 = 1
2. Một công ty sản xuất lốp xe đã lưu hồ sơ về quãng đường đã đi trước khi cần thay lốp. Bảng cho thấy kết quả của 1000 trường hợp.
| Khoảng cách (tính bằng km) | Dưới 4000 | 4000 đến 9000 | 9001 đến 14000 | Hơn 14000 |
| Tần số | 20 | 210 | 325 | 445 |
Nếu một chiếc lốp được mua từ công ty này, xác suất để:
(i) nó phải được thay thế trước khi 4000 km được bao phủ?
(ii) nó sẽ kéo dài hơn 9000 km?
(iii) nó phải được thay thế sau 4000 km và 14000 km được bảo hành?
Giải: (i) Tổng số lần thử = 1000.
Tần suất thay lốp trước khi đi 4000 km = 20
Vì vậy, P (E 1 ) = 20/1000 = 0,02
(ii) Tần suất mà lốp sẽ chạy hơn 9000 km = 325 + 445 = 770
Vì vậy, P (E 2 ) = 770/1000 = 0,77
(iii) Tần suất lốp cần thay từ 4000 km đến 14000 km = 210 + 325 = 535.
Vì vậy, P (E 3 ) = 535/1000 = 0,535
3. Phần trăm điểm của học sinh đạt được trong các bài kiểm tra hàng tháng được cho dưới đây:
| Kiểm tra | 1 | 2 | 3 | 4 | 5 |
| Phần trăm điểm đạt được | 69 | 71 | 73 | 68 | 74 |
Dựa vào bảng trên, hãy tìm xác suất để học sinh đạt trên 70% điểm trong một bài kiểm tra.
Bài giải: Tổng số bài kiểm tra đã thực hiện là 5 bài.
Số bài kiểm tra học sinh đạt trên 70% điểm = 3.
Vì vậy, P (đạt hơn 70% điểm) = ⅗ = 0,6
4. Một lá bài được rút ra từ bộ bài 52 lá, được xáo trộn tốt. Tính xác suất để thẻ
(i) là một át chủ bài,
(ii) không phải là một át chủ bài.
Giải pháp: Việc xáo trộn tốt đảm bảo các kết quả có khả năng xảy ra như nhau.
(i) Có 4 quân Át trong một bộ bài.
Gọi E là sự kiện lá bài được rút ra là át chủ bài.
Số lượng kết quả thuận lợi cho sự kiện E = 4
Số kết quả có thể xảy ra = 52
Do đó, P (E) = 4/52 = 1/13
(ii) Gọi F là trường hợp ‘quân bài không phải là quân át chủ bài’
Số kết quả thuận lợi cho F = 52 – 4 = 48
Số kết quả có thể xảy ra = 52
Do đó, P (F) = 48/52 = 12/13
| Sự kiện bổ sung: Nếu P (E) là xác suất của một sự kiện và P (không phải E) là xác suất của một sự kiện không xảy ra, thì:
P (E) + P (không phải E) = 1 P (không phải E) = 1-P (E) |
5. Hai người chơi, Sangeet và Rashmi, chơi một trận quần vợt. Xác suất để Sangeet thắng trận là 0,62. Xác suất để Rashmi thắng trận đấu là bao nhiêu?
Giải: Gọi S và R là các biến cố mà Sangeeta thắng trận và Reshma thắng trận tương ứng.
Xác suất để Sangeet thắng = P (S) = 0,62
Xác suất để Rashmi thắng = P (R) = 1 – P (S)
= 1 – 0,62 = 0,38
| Kết quả: Một kết quả có thể có của một thử nghiệm ngẫu nhiên.
Không gian mẫu: Tập hợp các kết quả trong một thử nghiệm ngẫu nhiên Điểm mẫu: Mỗi phần tử của không gian mẫu Ví dụ: Nói, lăn một con súc sắc. Kết quả = 1,2,3,4,5 hoặc 6 Không gian mẫu = {1,2,3,4,5,6} |
6. Hai đồng xu (một đồng một rupee và một đồng hai rupee) được tung một lần. Tìm một không gian mẫu.
Giải pháp: Đầu (H) hoặc Đuôi (T) có thể là kết quả.
Đầu trên cả hai đồng tiền = (H, H) = HH
Đầu trên đồng 1 và Đuôi trên đồng 2 = (H, T) = HT
Đuôi trên đồng 1 và Đầu trên đồng 2 = (T, H) = TH
Đuôi trên cả hai đồng tiền = (T, T) = TT
Do đó, không gian mẫu là S = {HH, HT, TH, TT}
7. Hãy xem xét thí nghiệm trong đó một đồng xu được tung nhiều lần cho đến khi một cái đầu nhô lên. Mô tả không gian mẫu.
Giải pháp: Trong thử nghiệm ngẫu nhiên, đầu có thể xuất hiện ở lần tung thứ nhất, hoặc lần tung thứ hai, hoặc lần tung thứ 3, v.v. cho đến khi chúng ta nhận được đầu đồng xu. Do đó, không gian mẫu được yêu cầu là:
S = {H, TH, TTH, TTTH, TTTTH,…}
8. Hãy xem xét thí nghiệm lăn một con súc sắc. Gọi A là biến cố ‘nhận được số nguyên tố’, B là biến cố ‘nhận được số lẻ’. Viết các tập hợp đại diện cho các sự kiện
(i) Aor B
(ii) A và B
(iii) A nhưng không phải B
(iv) ‘không phải A’.
Lời giải: S = {1, 2, 3, 4, 5, 6}, A = {2, 3, 5} và B = {1, 3, 5}
(i) A hoặc B = A ∪ B = {1, 2, 3, 5}
(ii) A và B = A ∩ B = {3,5}
(iii) A nhưng không phải B = A – B = {2}
(iv) không phải A = A ′ = {1,4,6}
9. Một đồng xu được tung ba lần, hãy xem xét các sự kiện sau.
P: ‘Không có đầu xuất hiện’,
Q: ‘Đúng một cái đầu xuất hiện’ và
R: ‘Ít nhất hai cái đầu xuất hiện’.
Kiểm tra xem chúng có tạo thành một tập hợp các sự kiện loại trừ lẫn nhau và toàn diện hay không.
Bài giải: Không gian mẫu của thí nghiệm là:
S = {HHH, HHT, HTH, THH, HTT, THT, TTH, TTT} và
P = {TTT},
Q = {HTT, THT, TTH},
R = {HHT, HTH, THH, HHH}
P ∪ Q ∪ R = {TTT, HTT, THT, TTH, HHT, HTH, THH, HHH} = S
Do đó, P, Q và R là các sự kiện toàn phần.
Và
P ∩ Q = φ,
P ∩ R = φ và
Q ∩ R = φ
Do đó, các sự kiện là rời rạc từng cặp, tức là chúng loại trừ lẫn nhau.
Do đó, P, Q và R tạo thành một tập hợp các sự kiện loại trừ lẫn nhau và tổng thể.
| Xác suất có điều kiện: Xác suất này của biến cố E được gọi là xác suất có điều kiện của E cho rằng F đã xảy ra, và được ký hiệu là P (E | F).
P (E | F) = Số sự kiện sơ cấp có lợi cho E∩F / Số sự kiện sơ cấp có lợi cho F P (E | F) = n (E∩F) / n (F) Hoặc là P (E | F) = P (E∩F) / P (F) trong đó P (F) ≠ 0 |
10. Nếu P (A) = 7/13, P (B) = 9/13 và P (A∩B) = 4/13, hãy đánh giá P (A | B).
Giải: P (A | B) = P (A∩B) / P (B) = (4/13) / (9/13) = 4/9
Xem thêm :
Sự khác biệt giữa lỗi thời gian biên dịch và lỗi thời gian chạy