Kiểm tra thêm các công thức toán học tại đây.
Contents
Công thức tính diện tích tam giác cân là gì?
Tổng diện tích được bao phủ bởi một tam giác cân được gọi là diện tích của nó. Đối với một tam giác cân, có thể dễ dàng tính được diện tích nếu biết chiều cao (tức là đường cao) và cơ sở. Nhân chiều cao với cơ sở rồi chia cho 2, ta được diện tích tam giác cân.
Tam giác cân là gì?
Tam giác cân là tam giác có độ dài ít nhất hai cạnh bằng nhau. Tính chất này tương đương với hai góc của tam giác bằng nhau. Một tam giác cân có hai cạnh bên bằng nhau và hai góc bằng nhau. Tên bắt nguồn từ tiếng Hy Lạp iso (giống nhau) và Skelos (chân). Tam giác đều là một trường hợp đặc biệt của tam giác cân mà cả ba cạnh và góc của tam giác đều bằng nhau.
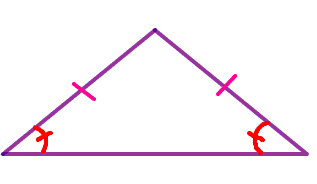

Một tam giác cân có độ dài hai cạnh bên bằng nhau và hai góc bằng nhau, các góc mà các cạnh này gặp cạnh thứ ba là hình đối xứng. Nếu kẻ một đường vuông góc từ giao điểm của hai cạnh bằng nhau đến đáy của cạnh không bằng nhau thì tạo ra hai tam giác vuông.
Diện tích của Công thức tam giác cân
Diện tích của một tam giác cân được cho bởi công thức sau:
| Diện tích = ½ × cơ sở × Chiều cao |
Cũng thế,
| Chu vi của tam giác cân | P = 2a + b |
| Đường cao của tam giác cân | h = √ (a 2 – b 2/4 ) |
Danh sách các công thức để tìm diện tích tam giác cân
| Công thức tìm diện tích tam giác cân | |
|---|---|
| Sử dụng cơ sở và chiều cao | A = ½ × b × h |
| Sử dụng cả ba mặt | A = ½ [√ (a 2 – b 2 ⁄4) × b] |
| Sử dụng độ dài của 2 cạnh và góc giữa chúng | A = ½ × b × c × sin (α) |
| Sử dụng hai góc và độ dài giữa chúng | A = [c 2 × sin (β) × sin (α) / 2 × sin (2π − α − β)] |
| Công thức diện tích của một tam giác vuông cân | A = ½ × a 2 |
Làm thế nào để tính diện tích nếu chỉ biết các mặt của tam giác cân?
Nếu biết độ dài các cạnh bằng nhau và độ dài đáy của một tam giác cân, thì chiều cao hoặc đường cao của tam giác sẽ được tính theo công thức sau:
| Cao độ của tam giác cân = √ (a 2 – b 2/4 ) |
Vì vậy,
| Diện tích Tam giác cân Chỉ sử dụng các cạnh = ½ [√ (a 2 – b 2/4 ) × b] |
Đây,
- b = cơ sở của tam giác cân
- h = chiều cao của tam giác cân
- a = độ dài hai cạnh bằng nhau
Tính xác định diện tích tam giác cân bằng công thức Heron
Có thể dễ dàng suy ra diện tích của một tam giác cân bằng công thức Heron như được giải thích bên dưới.
Theo công thức của Heron,
Diện tích = √ [s (s − a) (s − b) (s − c)]
Trong đó, s = ½ (a + b + c)
Bây giờ, đối với một tam giác cân,
s = ½ (a + a + b)
⇒ s = ½ (2a + b)
Hoặc, s = a + (b / 2)
Hiện nay,
Diện tích = √ [s (s − a) (s − b) (s − c)]
Hoặc, Diện tích = √ [s (s − a) 2 (s − b)]
⇒ Diện tích = (s − a) × √ [s (s − b)]
Thay thế giá trị của “s”
⇒ Diện tích = (a + b / 2 – a) × √ [(a + b / 2) × ((a + b / 2) – b)]
⇒ Diện tích = b / 2 × √ [(a + b / 2) × (a – b / 2)]
Hoặc, diện tích tam giác cân = b / 2 × √ (a 2 – b 2/4 )
Diện tích của Tam giác vuông cân Công thức
| Công thức tính Diện tích tam giác vuông cân = ½ × a 2 |
Nguồn gốc:
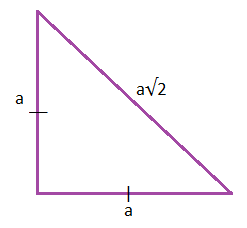
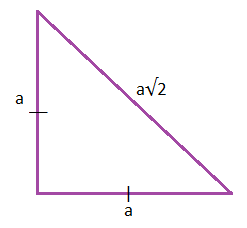
Diện tích = ½ × cơ sở × chiều cao
diện tích = ½ × a × a = a 2 /2
Chu vi của Công thức tam giác vuông cân
| P = a (2 + √2) |
Nguồn gốc:
Chu vi của một tam giác vuông cân là tổng tất cả các cạnh của một tam giác vuông cân.
Giả sử hai cạnh bằng nhau là a. Sử dụng định lý Pythagoras, tìm thấy cạnh không bằng nhau là a√2.
Do đó, chu vi tam giác vuông cân = a + a + a√2
= 2a + a√2
= a (2 + √2)
= a (2 + √2)
Diện tích tam giác cân bằng lượng giác
Sử dụng chiều dài của 2 mặt và góc giữa chúng
A = ½ × b × c × sin (α)
Sử dụng 2 góc và độ dài giữa chúng
A = [c 2 × sin (β) × sin (α) / 2 × sin (2π − α − β)]
Câu hỏi ví dụ
Câu 1: Tìm diện tích tam giác cân đã cho có b = 12 cm và h = 17 cm?
Giải pháp:
Cơ sở của tam giác (b) = 12 cm
Chiều cao của hình tam giác (h) = 17 cm
Diện tích Tam giác cân = (1/2) × b × h
= (1/2) × 12 × 17
= 6 × 17
= 102 cm 2
Câu 2: Tìm độ dài đáy của một tam giác cân có diện tích là 243 cm 2 và đường cao của tam giác là 27 cm.
Giải pháp:
Diện tích tam giác = A = 243 cm 2
Chiều cao của hình tam giác (h) = 27 cm
Cơ sở của tam giác = b =?
Diện tích Tam giác cân = (1/2) × b × h
243 = (1/2) × b × 27
243 = (b × 27) / 2
b = (243 × 2) / 27
b = 18 cm
Như vậy, đáy của tam giác là 18 cm.
Câu 3: Tìm diện tích, đường cao và chu vi của một tam giác cân đã cho a = 5 cm (độ dài hai cạnh bằng nhau), b = 9 cm (đáy).
Giải pháp:
Cho trước, a = 5 cm
b = 9 cm
Chu vi tam giác cân
= 2a + b
= 2 (5) + 9 cm
= 10 + 9 cm
= 19 cm
Độ cao của tam giác cân
h = √ (a 2 – b 2/4 )
= √ (5 2 – 9 2/4 )
= √ (25 – 81/4) cm
= √ (25–81 / 4) cm
= √ (25−20,25) cm
= √4.75 cm
h = 2,179 cm
Diện tích tam giác cân
= (b × h) / 2
= (9 × 2,179) / 2 cm²
= 19,611 / 2 cm²
A = 9,81 cm²
Câu 4 : Tìm diện tích, đường cao và chu vi của một tam giác cân đã cho có a = 12 cm, b = 7 cm.
Giải pháp :
Được,
a = 12 cm
b = 7 cm
Chu vi tam giác cân
= 2a + b
= 2 (12) + 7 cm
= 24 + 7 cm
P = 31 cm
Độ cao của tam giác cân
= √ (a 2 – b 2 ⁄4)
= √ (12 2 −7 2/4 ) cm
= √ (144−49 / 4) cm
= √ (144−12,25) cm
= √131,75 cm
h = 11,478 cm
Diện tích tam giác cân
= (b × h) / 2
= (7 × 11,478) / 2 cm²
= 80.346 / 2 cm²
= 40,173 cm²
Các câu hỏi thường gặp
Tam giác cân là gì?
Tam giác cân có thể được định nghĩa là một loại tam giác đặc biệt có số đo 2 cạnh bằng nhau. Đối với một tam giác cân, cùng với hai cạnh là hai góc cũng có số đo bằng nhau.
Diện tích của một tam giác cân có nghĩa là gì?
Diện tích tam giác cân được định nghĩa là khoảng không gian mà tam giác cân chiếm trong mặt phẳng hai chiều.
Công thức tính diện tích tam giác cân là gì?
Để tính diện tích của một tam giác đều, sử dụng công thức sau:
A = ½ × b × h
Công thức tính chu vi của tam giác cân là gì?
Công thức tính chu vi hình tam giác đều là:
P = 2a + b