Làm thế nào để tìm các góc của một đa giác nhanh chóng nhất

Đa giác không chỉ có các cạnh. Có thể có tình huống khi bạn có nhiều hơn một hình dạng với cùng số cạnh.

Làm thế nào để phân biệt chúng sau đó?
ANGLES!

Ví dụ đơn giản nhất là cả hình chữ nhật và hình bình hành đều có 4 cạnh, các cạnh đối diện song song và có độ dài bằng nhau. Sự khác biệt nằm ở các góc, trong đó một hình chữ nhật có các góc 90 độ ở cả 4 cạnh của nó trong khi một hình bình hành có các góc đối diện có số đo bằng nhau.

Trong bài viết này, bạn sẽ tìm hiểu về:

• Làm thế nào để tìm góc của một đa giác?
• Các góc bên trong của một đa giác.
• Các góc ngoại tiếp của một đa giác.
• Làm thế nào để tính kích thước của mỗi góc trong và ngoài của một đa giác đều?

Làm thế nào để tìm các góc của một đa giác?

Chúng ta biết rằng một đa giác là một hình đa diện hai chiều được tạo thành từ các đoạn thẳng . Tổng các góc của một đa giác là tổng số đo của tất cả các góc bên trong của một đa giác.

Vì tất cả các góc bên trong đa giác đều bằng nhau, do đó, công thức tìm các góc của một đa giác đều được cho bởi;

Tổng các góc bên trong = 180 ° * (n – 2)

Trong đó n = số cạnh của đa giác.

Các ví dụ

• Các góc của một tam giác:

một tam giác có 3 cạnh, do đó,

n = 3

Thay n = 3 vào công thức tìm các góc của đa giác.

Tổng các góc bên trong = 180 ° * (n – 2)

= 180 ° * (3 – 2)

= 180 ° * 1

= 180 °

• Các góc của một tứ giác:

Một tứ giác là một đa giác có 4 cạnh, do đó,

n = 4.

Bằng cách thay thế,

tổng các góc = 180 ° * (n – 2)

= 180 ° * (4 – 2)

= 180 ° * 2

= 360 °

• Góc của Lầu Năm Góc

Ngũ giác là một đa giác 5 cạnh.

n = 5

Người thay thế.

Tổng các góc bên trong = 180 ° * (n – 2)

= 180 ° * (5 – 2)

= 180 ° * 3

= 540 °

• Các góc của một hình bát giác.

Hình bát giác là một hình đa giác 8 cạnh

n = 8

Bằng cách thay thế,

Tổng các góc bên trong = 180 ° * (n – 2)

= 180 ° * (8 – 2)

= 180 ° * 6

= 1080 °

Các góc của một Hectagon:

một Hectagon là một đa giác 100 cạnh.

n = 100.

Người thay thế.

Tổng các góc bên trong = 180 ° * (n – 2)

= 180 ° * (100 – 2)

= 180 ° * 98

= 17640 °

Xem thêm:

Cách tính chu vi của đa giác chưa đầy 1 nốt nhạc

Đa giác – Giải thích & Ví dụ chưa bao giờ đơn giản đến thế!

Góc trong của đa giác

Góc trong của một đa giác là một góc được tạo thành bên trong một đa giác và nó nằm giữa hai cạnh của một đa giác.

Số cạnh của một đa giác bằng số góc tạo thành trong một đa giác cụ thể. Kích thước của mỗi góc trong của một đa giác được cho bởi;

Số đo của mỗi góc bên trong = 180 ° * (n – 2) / n

trong đó n = số cạnh.

Các ví dụ

• Kích thước góc trong của hình lục giác.

Một hình lục giác là một đa giác 10 cạnh.

n = 10

Số đo của mỗi góc bên trong = 180 ° * (n – 2) / n

Thay thế.

= 180 ° * (10 – 2) / 10

= 180 ° * 8/10

= 18 ° * 8

= 144 °

• Góc bên trong của một hình lục giác.

Một hình lục giác có 6 cạnh, do đó, n = 6

Người thay thế.

Số đo của mỗi góc bên trong = 180 ° * (n – 2) / n

= 180 ° * (6 – 2) / 6

= 180 ° * 4/6

= 60 ° * 2

= 120 °

• Góc bên trong của hình chữ nhật

Hình chữ nhật là một ví dụ về hình tứ giác (4 cạnh)

n = 4

Số đo của mỗi góc bên trong = 180 ° * (n – 2) / n

= 180 ° * (4 – 2) / 4

= 180 ° * 1/2

= 90 °

• Góc nội tiếp của hình ngũ giác.

Một hình ngũ giác bao gồm 5 cạnh.

n = 5

Số đo của mỗi góc bên trong = 180 ° * (5 – 2) / 5

= 180 ° * 3/5

= 108 °

Góc ngoại thất của đa giác

Góc bên ngoài của một đa giác là góc được tạo thành bên ngoài một đa giác nằm giữa một mặt bên và một mặt kéo dài. Số đo của mỗi góc bên ngoài của một đa giác đều được cho bởi;

Số đo của mỗi góc bên ngoài = 360 ° / n; trong đó, n = số cạnh của một đa giác.

Một tính chất quan trọng về các góc bên ngoài của một đa giác đều là tổng số đo các góc bên ngoài của một đa giác luôn là 360 °.

Các ví dụ

• Góc ngoại tiếp của tam giác:

Đối với một tam giác, n = 3

Người thay thế.

Số đo của mỗi góc bên ngoài = 360 ° / n

= 360 ° / 3

= 120 °

• Góc ngoại thất của Lầu Năm Góc:

n = 5

Số đo của mỗi góc bên ngoài = 360 ° / n

= 360 ° / 5

= 72 °

LƯU Ý: Công thức góc bên trong và góc bên ngoài chỉ hoạt động đối với đa giác đều. Đa giác không đều có số đo góc bên trong và bên ngoài khác nhau.

Chúng ta hãy xem xét các bài toán ví dụ khác về các góc bên trong và bên ngoài của đa giác.

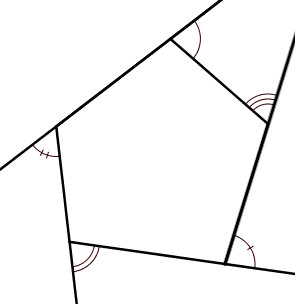
ví dụ 1

Các góc bên trong của một đa giác 6 cạnh không đều là; 80 °, 130 °, 102 °, 36 °, x ° và 146 °.

Tính độ lớn của góc x trong đa giác.

Giải pháp

Đối với một đa giác có 6 cạnh, n = 6

tổng các góc bên trong = 180 ° * (n – 2)

= 180 ° * (6 – 2)

= 180 ° * 4

= 720 °

Do đó, 80 ° + 130 ° + 102 ° + 36 ° + x ° + 146 ° = 720 °

Đơn giản hóa.

494 ° + x = 720 °

Trừ 494 ° cho cả hai bên.

494 ° – 494 ° + x = 720 ° – 494 °

x = 226 °

Ví dụ 2

Tìm góc ngoại tiếp của một đa giác đều có 11 cạnh.

Giải pháp

n = 11

Số đo của mỗi góc bên ngoài = 360 ° / n

= 360 ° / 11

≈ 32,73 °

Ví dụ 3:

Các góc bên ngoài của một đa giác là; 7x °, 5x °, x °, 4x ° và x °. Xác định giá trị của x.

Giải pháp

Tổng ngoại cảnh = 360 °

7x ° + 5x ° + x ° + 4x ° + x ° = 360 °

Đơn giản hóa.

18x = 360 °

Chia cả hai bên cho 18.

x = 360 ° / 18

x = 20 °

Do đó, giá trị của x là 20 °.

Ví dụ 4

Tên của một đa giác có các góc trong của mỗi góc là 140 °?

Giải pháp

Kích thước của mỗi góc bên trong = 180 ° * (n – 2) / n

Do đó, 140 ° = 180 ° * (n – 2) / n

Nhân cả hai vế với n

140 ° n = 180 ° (n – 2)

140 ° n = 180 ° n – 360 °

Trừ cả hai vế đi 180 ° n.

140 ° n – 180 ° n = 180 ° n – 180 ° n – 360 °

-40 ° n = -360 °

Chia cả hai bên -40 °

n = -360 ° / -40 °

= 9.

Do đó, số cạnh là 9 (nonagon).

Câu hỏi thực hành

1. Bốn góc bên trong đầu tiên của một hình ngũ giác là tất cả và góc thứ năm là 140 °. Tìm số đo của bốn góc.
2. Tìm số đo tám góc của một đa giác nếu bảy góc đầu tiên là 132 ° mỗi góc.
3. Tính các góc của một đa giác mà ae đã cho; (x – 70) °, x °, (x – 5) °, (3x – 44) ° và (x + 15) °.
4. Tỉ số các góc của một lục giác là; 1: 2: 3: 4: 6: 8. Tính số đo các góc.
5. Tên của một đa giác có mỗi góc trong là 135 °?