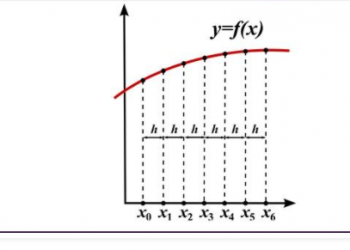
• Tích phân xác định
• Không xác định, không thể thiếu

Trong bài này, chúng ta sẽ thảo luận về định nghĩa của tích phân xác định và quá trình đánh giá tích phân xác định bằng cách sử dụng các tính chất khác nhau.

Tích phân xác định là gì?

Nếu giới hạn trên và giới hạn dưới của biến độc lập của hàm hoặc tích phân đã cho được chỉ định, thì tích phân của nó được biểu thị bằng cách sử dụng các tích phân xác định. Một tích phân xác định được ký hiệu là:

F( a ) – F( b ) =∫abf( x ) dxỞ đây RHS của phương trình có nghĩa là tích phân của f (x) đối với x.

f (x) được gọi là tích phân.

dx được gọi là tác nhân tích phân.

a là giới hạn trên của tích phân và b là giới hạn dưới của tích phân.

Đánh giá Tích phân xác định – Thuộc tính

Bây giờ chúng ta hãy thảo luận về các tính chất quan trọng của tích phân xác định và cách chứng minh chúng.

Thuộc tính 1: ∫abf (x) dx = ∫abf (t) dt

Chúng ta hãy xem xét x = t. Do đó dx = dt. Thay các giá trị này vào LHS của phương trình trên ta có thể chứng minh được tính chất này.

Thuộc tính 2: ∫abf (x) dx = –∫baf (x) dx

Theo định lý cơ bản thứ hai của Giải tích , nếu f (x) là một hàm liên tục xác định trên khoảng đóng [a, b] và F (x) là phản đạo hàm của f (x) thì

∫abf (x) dx = [F (x)]ba= F (b) -F (a)

vì thế

∫abf (x) dx = F (b) -F (a) = – [F (a) -F (b) = –∫baf (x) dx

Thuộc tính 3: ∫abdx = ∫acf (x) dx + ∫cbf (x) dx

Từ định lý thứ hai của Giải tích,

∫abf (x) dx = [F (x)]ba= F (b) -F (a)

Vì thế,

∫abf (x) dx = F (b) -F (a) ——- (1)

∫acf (x) dx = F (c) -F (a) ——- (2)

∫cbf (x) dx = F (b) -F (c) ——- (3)

Thêm phương trình 2 và 3 chúng ta có

∫acf (x) dx + ∫cbf (x) dx = F (c) -F (a) + F (b) -F (c) = F (b) -F (a) =∫abf (x) dx

Thuộc tính 4:  ∫abf (x) dx = ∫abf (a + bx) dx

Giả sử t = a + b – x. Do đó dt = -dx. Tại x = a, t = b và tại x = b, t = a.

Vì thế,
∫abf (x) dx = –∫baf (a + bt) dt

Từ tính chất thứ hai của tích phân xác định:
∫abf (x) dx = –∫baf (x) dx

Vì thế,
∫abf (x) dx = –∫baf (a + bt) dt =∫abf (a + bt) dt

Theo tính chất đầu tiên của tích phân xác định:
∫abf (x) dx = ∫abf (a + bx) dx

Thuộc tính 5: ∫0af (x) dx =∫0af (ax) dx

Tính chất này là một trường hợp đặc biệt của tính chất thứ tư của tích phân như đã thảo luận ở trên.
Giả sử rằng t = a – x. Do đó dt = -dx. Tại x = 0, t = a và tại x = a, t = 0.

Vì thế,
∫0af (x) dx = ∫a0f (at) dt

Từ tính chất thứ hai của tích phân xác định:
∫0af (x) dx = –∫0af (x) dx

Vì thế,
∫0af (x) dx = –∫a0f (at) dt =∫0af (at) dt

Theo tính chất đầu tiên của tích phân xác định:
∫0af (x) dx =∫0af (ax) dx

Thuộc tính 6: ∫02 af (x) dx =∫0af (x) f (x) dx +∫0af (2a-x) dx

Từ tính chất thứ hai của tích phân xác định
∫abf (x) dx = ∫acf (x) dx +∫cbf (x) dx

Vì thế,
∫02 af (x) dx =∫0af (x) dx +∫a2 af (x) dx ——– (4)

Giả sử t = 2a – x. Khi đó dt = – dx. Trong trường hợp này, khi x = 2a, t = 0. Do đó, tích phân thứ hai có thể được biểu thị là:

∫a2 af (x) dx = ∫a0f (2a-t) dt =∫0af (2a-t) dt =∫0af (2a-x) dx

Do đó, phương trình 4 có thể được viết lại thành:
∫02 af (x) dx =∫0af (x) dx +∫0af (2a-x) dx

Thuộc tính 7:  ∫02 af (x) dx = 2∫0af (x) dx nếu f (2a-x) = f (x) và ∫02 af (x) dx = 0 nếu f (2a-x) = – f (x)

Sử dụng tính chất thứ sáu của tích phân xác định, chúng ta có
∫02af (x) dx =∫0af (x) dx +∫0af (2a-x) dx ——- (5)

Nếu trong trường hợp f (2a-x) = f (x), thì phương trình 5 có thể được viết lại thành:
∫02 af (x) dx =∫0af (x) dx +∫0af (x) dx

Nếu f (2a – x) = -f (x), thì phương trình 5 có thể được viết lại thành:
∫02 af (x) dx =∫0af (x) dx –∫0af (x) dx

Thuộc tính 8: ∫– mộtaf (x) dx = 2∫0af (x) dx nếu f (-x) = f (x) và ∫– mộtaf (x) dx = 0 nếu f (-x) = -f (x)

Sử dụng tính chất thứ ba của tích phân xác định, chúng ta có
∫abf (x) dx =∫acf (x) dx +∫cbf (x) dx

Vì thế,
∫– mộtaf (x) dx =∫– một0f (x) dx +∫0af (x) dx ——– (6)

Giả sử rằng t = -x. Khi đó dt = -dx. Do đó khi x = -a, t = a và x = 0, t = 0. Khi đó tích phân đầu tiên trong vế phải có thể được viết thành:
∫– một0f (x) dx = –∫a0f (-t) dt

Do đó phương trình 6 có thể được viết thành;
∫– mộtaf (x) dx = –∫a0f (-t) dt + ∫0af (x) dx

∫– mộtaf (x) dx = ∫0af (-x) dx + ∫0af (x) dx ——— (7)

Trong trường hợp nếu f là hàm chẵn, tức là f (-x) = f (x), thì phương trình 7 có thể được viết lại thành:
∫– mộtaf (x) dx = ∫0af (x) dx + ∫0af (x) dx = 2∫0af (x) dx

Trong trường hợp nếu f là một hàm lẻ, tức là f (-x) = – f (x), thì phương trình 7 có thể được viết lại thành:
∫– mộtaf (x) dx = ∫0af (x) dx- ∫0af (x) dx = 0