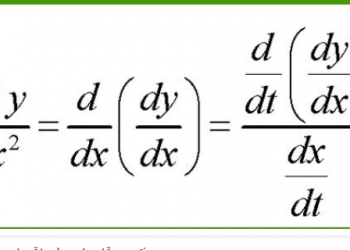Cách tìm đạo hàm của hàm
Nếu f là một hàm có giá trị thực và ‘a’ là bất kỳ điểm nào trong miền của nó mà f được xác định thì f (x) được cho là khả vi tại điểm x = a nếu đạo hàm f ‘(a) tồn tại tại mọi điểm trong miền của nó. Nó được đưa ra bởi
f′( a ) =limh → 0f( a + h ) – f( a )h
Cho rằng tồn tại giới hạn này và f ‘(a) biểu diễn đạo hàm của f (x) tại a. Đây là nguyên lý đầu tiên của đạo hàm.
Miền của f ‘(a) được xác định bởi sự tồn tại của các giới hạn của nó. Đạo hàm cũng được ký hiệu là . Nếu y = f (x) thì đạo hàm của f (x) được cho dưới dạng hoặc y ‘.ddx, f( x )o rD ( f( x ) )
dd x
Đây được gọi là đạo hàm của y đối với x.
Ngoài ra, đạo hàm của hàm số f theo x tại x = a được cho là:
dd xf( x )|x = a hoặcd fd x|x = a
Đạo hàm của hàm f (x) biểu thị tốc độ thay đổi của hàm f (x) đối với x tại một điểm nằm trong miền của nó. Để một hàm có thể phân biệt được tại bất kỳ điểm nào x = a trong miền của nó, thì hàm đó phải liên tục tại điểm cụ thể đó nhưng ngược lại không nhất thiết phải luôn đúng.
Đại số các Đạo hàm
Quá trình xác định đạo hàm của một hàm được gọi là phân biệt. Có thể thấy rõ rằng khái niệm cơ bản về đạo hàm của một hàm số gắn bó chặt chẽ với các giới hạn. Do đó, có thể mong đợi rằng các quy tắc của phái sinh tương tự như các quy tắc của giới hạn. Các quy tắc sau là một phần của đại số các đạo hàm:
Coi f và g là hai hàm có giá trị thực sao cho sự khác biệt của các hàm này được xác định trong một miền chung. Sau đó,
- Tổng các đạo hàm của các hàm f và g bằng đạo hàm của tổng của chúng, tức là
dd x[ f( x ) + g( x ) ] =dd xf( x ) +dd xg( x )
Đặt u = f (x) và v = g (x) thì (u + v) ‘= u’ + v ‘
- Hiệu của đạo hàm của các hàm f và g bằng đạo hàm của hiệu của các hàm này, tức là,
dd x[ f( x ) – g( x ) ] =dd xf( x ) –dd xg( x )
Đặt u = f (x) và v = g (x) thì (u – v) ‘= u’ – v ‘
- Đạo hàm của tích hai hàm f và g được cho bởi quy tắc tích như sau, nghĩa là
dd x[ f( x ) . g( x ) ] =g( x )dd xf( x ) + f( x )dd xg( x )
Đặt u = f (x) và v = g (x), sau đó quy tắc tích có thể được trình bày lại thành
(uv) ‘= u’v + uv’
Đây còn được gọi là quy tắc Leibnitz để phân biệt các sản phẩm của các chức năng
- Đạo hàm theo thương của hai hàm f và g được cho bởi quy tắc thương (với điều kiện mẫu số khác 0), tức là
dd xf( x )g( x )=g( x ) .d f( x )d x– f( x ) .dd xg( x )( g( x ))2
Cho u = f (x) và v = g (x), sau đó quy tắc thương có thể được trình bày lại thành
(uv)′=u′v – vu′v2
Quy tắc chuỗi:
Bất cứ khi nào đại lượng ‘y’ thay đổi với đại lượng ‘x’ khác sao cho y = f (x), thì f ‘(x) biểu thị tốc độ thay đổi của y đối với x (tại x = x 0 ). Ngoài ra, nếu hai biến ‘x’ và ‘y’ thay đổi so với biến thứ ba nói ‘t’ thì theo quy tắc chuỗi, chúng ta có
(d yd x) =d yd td td x,w h e r ed td x≠ 0
Hãy cùng chúng tôi xem xét một số ví dụ để có cái nhìn sâu sắc hơn.
| Hãy làm việc-
Ví dụ: Xác định tốc độ thay đổi thể tích của một khối cầu đối với bán kính ‘r’ của nó khi r = 3 cm. Giải pháp: Chúng ta biết Thể tích của một khối cầu là .43πr3 Tỷ lệ thay đổi Bán kính wrt khối lượng được cho là d Vd r=dd r(43πr3) =43× π( 3r2) d Vd r= 4 πr2 d Vd r∣( một tr = 3 )= 4 π( 3)2= 36 π < |
Xem thêm: