Giải bất đẳng thức một bước – Phương pháp & Ví dụ

Giải bất đẳng thức một bước

Trước khi chúng ta có thể học cách giải các bất đẳng thức một bước, chúng ta hãy tự nhắc nhở bản thân một vài thông tin cơ bản về bất đẳng thức.

Từ bất đẳng thức đơn giản có nghĩa là một biểu thức toán học trong đó các cạnh không bằng nhau. Về cơ bản, có năm ký hiệu bất đẳng thức được sử dụng để biểu diễn các phương trình bất đẳng thức.

Đó là:
nhỏ hơn ( < ),
lớn hơn ( > ),
nhỏ hơn hoặc bằng ( ≤ ),
lớn hơn hoặc bằng ( ≥ )
và ký hiệu không bằng ( ≠ ).

Bất đẳng thức được sử dụng để so sánh giữa các số và xác định phạm vi hoặc phạm vi giá trị thỏa mãn các điều kiện của một biến nhất định.

Làm thế nào để giải quyết bất bình đẳng một bước?

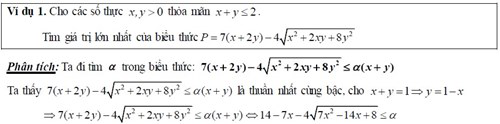
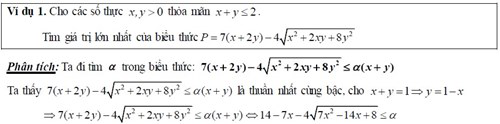
Giải bất đẳng thức một bước là một quá trình đơn giản như nó có vẻ. Chỉ cần một bước để giải hoàn toàn các phương trình.

Mục tiêu chính của việc giải bất đẳng thức một bước là cô lập một biến ở một phía của biểu tượng bất đẳng thức và cũng để làm cho hệ số của biến đó bằng một.

Các chiến lược cô lập một biến đòi hỏi việc sử dụng ngược lại hoạt động s. Ví dụ, để chuyển một số bị trừ khỏi vế còn lại của bất đẳng thức, bạn nên cộng.

Bước quan trọng nhất cần nhớ khi giải bất kỳ phương trình bất phương trình tuyến tính hoặc bất phương trình nào là thực hiện cùng một phép toán ở cả vế phải và vế trái của phương trình.

Nói cách khác, nếu bạn trừ hoặc cộng từ một vế của bất đẳng thức, thì bạn cũng phải trừ hoặc cộng với cùng giá trị với vế đối diện. Tương tự, nếu bạn nhân hoặc chia ở một vế của phương trình, thì bạn cũng phải nhân hoặc chia với cùng giá trị ở vế kia của phương trình.

Ngoại lệ duy nhất khi chia và nhân với một số âm trong bất phương trình là biểu tượng bất đẳng thức đảo ngược.

Chúng ta có thể tóm tắt các quy tắc để giải bất phương trình một bước như hình dưới đây:

• Trừ hoặc cộng cùng một số từ cả hai vế của một bất đẳng thức dẫn đến biểu tượng bất đẳng thức không thay đổi.
• Chia hoặc nhân cả hai vế với một số dương, kết quả là biểu tượng bất đẳng thức không thay đổi.
• Nhân hoặc chia cả hai vế với một số âm sẽ thay đổi bất bình đẳng. Điều này ngụ ý rằng, <thay đổi thành> và ngược lại.

Trong bài này, chúng ta sẽ đề cập đến năm trường hợp khác nhau để giải bất phương trình một bước. Những trường hợp bất đẳng thức một bước này dựa trên cách xử lý các phương trình.

Năm trường hợp bao gồm:

• Giải các bất bình đẳng một bước bằng phép cộng
• Giải các bất đẳng thức một bước bằng phép trừ
• Bất phương trình một bước được giải bằng cách nhân cả hai vế của phương trình với một số.
• Bất phương trình một bước được giải bằng cách chia cùng một số cho cả hai vế của phương trình.
• Bất phương trình một bậc được giải bằng cách nhân nghịch đảo của hệ số của số hạng với một biến cho cả hai vế của phương trình.

Xem thêm:

Bất đẳng thức phức hợp – Giải thích & Ví dụ

Vẽ đồ thị bất đẳng thức tuyến tính – Giải thích & Ví dụ

Giải bất phương trình một bước bằng cách thêm

Làm theo các bước trong các ví dụ dưới đây để hiểu điều này.

ví dụ 1

Giải phương trình một bước x – 4> 10

Giải pháp

Lưu ý rằng bên trái của biểu tượng bất đẳng thức có một biến x đang bị trừ đi 4, trong khi bên trái có một số dương 10. Trong trường hợp này, chúng ta sẽ giữ biến của chúng ta ở phía bên trái.

Để cô lập biến x, chúng ta cộng cả hai vế của phương trình với 4, cho kết quả;

x – 4 + 4> 10 +4

x> 14

Ví dụ 2

Giải ra  x  – 6> 14

Giải pháp

x – 6> 14

Cộng cả hai vế của phương trình với 6
x – 6 + 6> 14 + 6
x> 20

Ví dụ 3

Giải bất phương trình –7 – x <9

Giải pháp

–7 – x <9

Thêm 7 vào cả hai vế của phương trình.
7 – x + 7 <9 + 7
– x <16 Nhân cả hai vế với –1 và đảo dấu x> –16

Ví dụ 4

Giải 4> x  – 3

Giải pháp

Trong ví dụ này, biến nằm trên RHS của phương trình. Chúng ta có thể cô lập một biến trong một phương trình bất kể nó nằm ở đâu. Do đó, chúng ta chỉ cần để lại vế phải và để làm điều này, hãy thêm 3 vào cả hai vế của phương trình.

4+ 3> x  – 3 + 3

7> x

Và ở đó, chúng tôi đã hoàn thành!

Giải các bất đẳng thức một bước bằng phép trừ

Làm theo các bước trong các ví dụ dưới đây để hiểu điều này.

Ví dụ 5

Giải ra x + 10 <16

Giải pháp

x + 10 <16

Trừ 7 cho cả hai vế của phương trình.
x + 10 – 10 <16 – 10
x <6

Ví dụ 6

Giải bất phương trình 15> 26 – y

Giải pháp

15> 26 – y

Trừ 26 cho cả hai vế của phương trình
15 -26> 26 – 26 -y
– 11> -y

Nhân cả hai vế với –1 và đảo ngược dấu

11 <y

Ví dụ 7

Giải ra  x  + 6> –3

Giải pháp

Trừ cả hai vế cho 6.

x  + 6 – 6> –3 – 6

x  > – 9

Ví dụ 8

Giải phương trình một bước 13 <y + 8

Giải pháp

Trong trường hợp này, biến y cũng nằm ở vế phải của phương trình. Vậy được rồi! Chúng ta sẽ giữ bên trái bằng cách trừ cả hai bên đi 8.

13– 8 <y + 8 – 8

5 <y

Ví dụ 9

Giải cho t trong phương trình sau:

t + 18 <21

Giải pháp

Để cô lập t ở vế trái của phương trình, chúng ta trừ cả hai vế của phương trình đi 18.

t + 18 -18 <21 – 18

t <3

Giải bất phương trình một bước bằng cách nhân cả hai vế của phương trình với một số

Làm theo các bước trong các ví dụ dưới đây để hiểu điều này.

Ví dụ 10

Giải x trong phương trình một bước sau:

x / 4> 8

Giải pháp

Để loại bỏ một phân số, nhân cả hai vế của phương trình với mẫu số của phân số.

4 (x / 4)> 8 x 4

x> 32

Và đó là nó!

Ví dụ 11

Giải phương trình một bước -x / 5> 9

Giải pháp

Trong bất đẳng thức này, một biến x được chia cho 5. Vì mục tiêu của chúng ta là hoàn tác phép chia của biến, do đó chúng ta nhân cả hai vế của bất đẳng thức với

5 (-x / 5)> 9 x 5

-x> 45

Bây giờ nhân cả hai vế với -1 và đảo ngược dấu hiệu.

x <- 45

Ví dụ 11

Giải 2> –x

Giải pháp

Bạn có thể nhận thấy rằng, phương trình này gần như đã được giải. Nhưng không hoàn toàn. Vì vậy, chúng ta cần loại bỏ một dấu âm khỏi biến. Chúng ta có thể làm điều này bằng cách nhân cả hai vế của phương trình với -1 và đảo ngược dấu.

2 * -1> –x * -1

-2 <x

Giải bất phương trình một bậc bằng cách chia cùng một số cho cả hai vế của phương trình

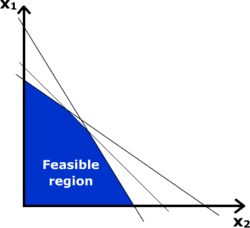
Làm theo các bước trong các ví dụ dưới đây để hiểu điều này.

Ví dụ 12

Giải cho x, 2x – 4 <0

Giải pháp

Thêm 4 cả hai bên

2x – 4 + 4 <0 + 4

2x <4

Chia mỗi bên cho 2, ta được

2x / 2 <4/2

x <4/2

Vì vậy, x <2 là câu trả lời!

Ví dụ 13

Giải phương trình một bước. 5x <100.

Giải pháp

Trong ví dụ này, một biến x đang được nhân với một số. Để hoàn tác phép nhân, chúng ta sẽ chia cả hai vế của phương trình cho hệ số của biến. Phép chia thường được sử dụng để hủy bỏ tác dụng của phép nhân.

5x / 5 <100/5

x <20

Ví dụ 14

21 <-3x

Giải pháp

Trong trường hợp này, biến nằm ở bên phải của phương trình, vì vậy đừng bận tâm đến việc hoán đổi phương trình. Vì hệ số của biến không bằng 1, điều này có nghĩa là chúng ta cần thực hiện một phép toán ngược lại để loại bỏ 3 khỏi -x. Vì vậy, chúng tôi sẽ chia cả hai bên cho -3.

21/3 <-3 / 3x

7 <-x Vì bất đẳng thức này không được đơn giản hóa nên chúng ta cần loại bỏ dấu âm khỏi biến. Do đó, chúng ta nhân cả hai vế của phương trình với -1 và đảo dấu. -7> x

Ví dụ 15

Giải ra −2x <4

Giải pháp

Để giải phương trình một bước này, chúng ta cần chia cả hai vế cho −2.

Vì chúng ta đang chia cả hai vế của phương trình cho một số âm, do đó chúng ta sẽ đảo ngược dấu bất đẳng thức.

x> -2

Ví dụ 16
Giải bất phương trình một bậc −2x> −8

Giải pháp

Chia cả hai vế của phương trình cho 2.

−2x / 2> −8/2

−x> – 4

Nhân cả hai vế với -1 và đảo dấu bất đẳng thức.

x <4

Giải bất phương trình một bậc bằng cách nhân nghịch đảo của hệ số biến với cả hai vế của phương trình.

Làm theo các bước trong các ví dụ dưới đây để hiểu điều này.

Ví dụ 17

Giải phương trình một bước (4x / 11) <4

Giải pháp

Nhiều người bị bỏ rơi khi được trình bày với bất đẳng thức một bước có chứa phân số.

Vì vậy, làm thế nào để chúng ta giải quyết loại vấn đề như vậy?

Vâng, chúng ta có thể giải các bất đẳng thức một bước mang phân số bằng cách nhân cả hai vế của phương trình với nghịch đảo của phân số. Trong trường hợp này, đối ứng của chúng tôi là 11/4.

(4x / 11) 11/4 <4 * 11/4

x <11

Câu hỏi thực hành

Giải các bất phương trình bậc một sau đây cho ẩn số.

1. 26 <8 + v
2. −15 + n> −9
3. 14b <−56
4. −6> b / 18
5. −15x <0
6. −17> x – 15
7. −16 + x <−15
8. n – 8> −10
9. m / 4> −13
10. −5 <a / 18