Giải phương trình giá trị tuyệt đối nhanh chóng nhất

Giá trị tuyệt đối là gì?

Giải phương trình chứa giá trị tuyệt đối cũng đơn giản như làm việc với phương trình tuyến tính thông thường . Trước khi chúng ta có thể bắt tay vào giải các phương trình giá trị tuyệt đối, chúng ta hãy xem xét ý nghĩa của từ giá trị tuyệt đối.

Trong toán học, giá trị tuyệt đối của một số đề cập đến khoảng cách của một số từ số 0, bất kể hướng. Giá trị tuyệt đối của một số x thường được biểu diễn dưới dạng | x | = a, ngụ ý rằng, x = + a và -a.

Chúng ta chỉ đơn giản nói rằng giá trị tuyệt đối của một số nhất định là phiên bản dương của số đó . Ví dụ, giá trị tuyệt đối của âm 5 là dương 5, và giá trị này có thể được viết là: | – 5 | = 5.

Các ví dụ khác về giá trị tuyệt đối của các số bao gồm: | – 9 | = 9, | 0 | = 0, – | −12 | = −12 v.v … Từ những ví dụ về giá trị tuyệt đối này, chúng ta chỉ cần định nghĩa phương trình giá trị tuyệt đối là phương trình chứa biểu thức với hàm giá trị tuyệt đối.

Làm thế nào để giải các phương trình giá trị tuyệt đối?

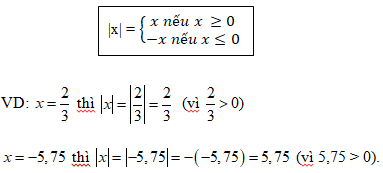
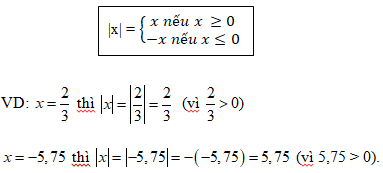
Sau đây là các bước tổng quát để giải phương trình chứa hàm giá trị tuyệt đối:

• Cô lập biểu thức chứa hàm giá trị tuyệt đối.
• Loại bỏ ký hiệu giá trị tuyệt đối bằng cách thiết lập hai phương trình sao cho trong phương trình thứ nhất, đại lượng bên trong ký hiệu tuyệt đối là dương và trong phương trình thứ hai là âm. Bạn sẽ loại bỏ ký hiệu tuyệt đối và chỉ ghi số lượng với ký hiệu phù hợp của nó.
• Tính giá trị chưa biết cho phiên bản dương của phương trình.
• Giải cho phiên bản âm của phương trình, trong đó trước tiên bạn sẽ nhân giá trị ở phía bên kia của dấu bằng với -1, rồi giải.

Ngoài các bước trên, có những quy tắc quan trọng khác bạn cần ghi nhớ khi giải phương trình giá trị tuyệt đối.

• ∣x∣ luôn dương: ∣x∣ → + x.
• Trong | x | = a, nếu  aở bên phải là số dương hoặc số 0 thì có một nghiệm.
• Trong | x | = a, nếu aở vế phải âm thì không có nghiệm.

ví dụ 1

Giải phương trình x: | 3 + x | – 5 = 4.

Giải pháp

• Cô lập biểu thức giá trị tuyệt đối bằng cách áp dụng định luật đẳng thức. Điều này có nghĩa là, chúng ta thêm 5 vào cả hai vế của phương trình để thu được;

| 3 + x | – 5 + 5 = 4 + 5

| 3 + x | = 9

• Tính toán cho phiên bản dương của phương trình. Giải phương trình bằng cách giả sử các ký hiệu giá trị tuyệt đối.

| 3 +  x  | = 9 → 3 +  x  = 9

Trừ 3 cho cả hai vế của phương trình.

3 – 3 + x = 9 -3

x = 6

• Bây giờ, hãy tính toán phiên bản âm của phương trình bằng cách nhân 9 với -1.

3 +  x  | = 9 → 3 +  x  = 9 × (−1)

3 + x = -9

Cũng trừ 3 ở cả hai bên để cô lập x.

3 -3 + x = – 9 -3

x = -12

Do đó 6 và -12 là nghiệm.

Ví dụ 2

Giải với mọi giá trị thực của x sao cho | 3x – 4 | – 2 = 3.

Giải pháp

• Cô lập phương trình với hàm tuyệt đối bằng cách cộng 2 vào cả hai vế.

= | 3x – 4 | – 2 + 2 = 3 + 2

= | 3x – 4 | = 5

Giả sử các dấu hiệu tuyệt đối và giải cho phiên bản dương của phương trình.

| 3x – 4 | = 5 → 3x – 4 = 5

Thêm 4 vào cả hai vế của phương trình.

3x – 4 + 4 = 5 + 4

3x = 9

Chia: 3x / 3 = 9/3

x = 3

Bây giờ giải cho phiên bản âm bằng cách nhân 5 với -1.

3x – 4 = 5 → 3x – 4 = -1 (5)

3x – 4 = -5

Thêm 4 vào cả hai vế của phương trình.

3x – 4 + 4 = – 5 + 4

3x = 1

Chia cho 3 ở cả hai bên.

3x / 3 = 1/3

x = 1/3

Do đó, 3 và 1/3 là giải pháp.

Ví dụ 3

Giải với mọi giá trị thực của x: Solve | 2 x  – 3 | – 4 = 3

Giải pháp

Thêm 4 cho cả hai bên.

| 2 x  – 3 | -4 = 3 → | 2 x  – 3 | = 7

Giả sử các ký hiệu tuyệt đối và giải cho phiên bản dương của x.

2 x  – 3 = 7

Thêm 3;

2x – 3 + 3 = 7 + 3

2x = 10

x = 5

Bây giờ giải cho phiên bản âm của x bằng cách nhân 7 với -1

2 x  – 3 = 7 → 2 x  – 3 = -1 (7)

2x -3 = -7

Thêm 3 vào cả hai bên.

2x – 3 + 3 = – 7 + 3

2x = -4

x = – 2

Do đó, x  = –2, 5

Xem thêm:

Cô lập biến (Chuyển vị) – Kỹ thuật & Ví dụ dễ hiểu nhất

Giải một biến trong một công thức – Phương trình chữ ai cũng học được

Ví dụ 4

Giải với mọi số thực của x: | x + 2 | = 7

Giải pháp

Biểu thức giá trị tuyệt đối đã bị cô lập, do đó giả sử các ký hiệu tuyệt đối và giải quyết.

| x + 2 | = 7 → x + 2 = 7

Trừ 2 cho cả hai bên.

x + 2 – 2 = 7 -2

x = 5

Nhân 7 với -1 để tìm phiên bản âm của phương trình.

x + 2 = -1 (7) → x + 2 = -7

Trừ đi 2 bên.

x + 2 – 2 = – 7 – 2

x = -9

Do đó, x = -9, 5

Câu hỏi thực hành

Giải các số thực của x trong mỗi phương trình sau:

1. ∣ x ∣ = −5
2. | 2x – 1 | + 3 = 6
3. | 5x + 4 | + 10 = 2
4. | 3x – 6 | – 9 = -3
5. ∣9 – 2x∣ + 9 = −12
6. ∣ − 6x + 3∣ − 7 = 20
7. 25∣ – 2x + 7∣ = 25
8. ∣x – 5∣ = 3
9. 4 | 2 x  – 3 | + 1 = 21
10. | 5x + 9 | = −3
11. | 5x + 9 | = −3