Cách giải một phương trình nhanh gọn trong vòng 1 nốt nhạc

Giải phương trình – Kỹ thuật & Ví dụ

Hiểu cách giải phương trình là một trong những kỹ năng cơ bản nhất mà mỗi sinh viên học đại số có thể nắm vững. Các giải pháp cho hầu hết các biểu thức đại số được tìm kiếm bằng cách áp dụng kỹ năng này, và do đó, học sinh trở nên thành thạo hơn về cách thực hiện phép toán là điều cần thiết.

Trong bài này, chúng ta sẽ học cách giải một phương trình bằng cách thực hiện bốn phép toán cơ bản là; cộng , trừ , nhân và chia .

Một phương trình thường bao gồm hai biểu thức được phân tách bằng dấu cho biết mối quan hệ của chúng. Các biểu thức trong một phương trình có thể liên quan với nhau bằng dấu (=), nhỏ hơn (<), lớn hơn (>) hoặc kết hợp của các dấu này.

Làm thế nào để giải phương trình?

Giải một phương trình đại số nói chung là quy trình thao tác một phương trình để biến số đó nằm ở một phía và mọi thứ khác nằm ở phía bên kia của phương trình.

Nói cách đơn giản, để giải một phương trình là cô lập bằng cách làm cho hệ số của nó bằng 1. Dù bạn làm gì với một vế của phương trình, hãy làm tương tự với vế đối diện của phương trình.

Giải phương trình bằng cách cộng

Hãy xem một vài ví dụ dưới đây để hiểu khái niệm này.

ví dụ 1

Giải: –7 – x = 9

Giải pháp

–7 – x = 9

Thêm 7 vào cả hai vế của phương trình.
7 – x + 7 = 9 + 7
– x = 16

Nhân cả hai vế với –1
x = –16

Ví dụ 2

Giải ra 4 = x – 3

Giải pháp

Ở đây, biến nằm trên RHS của phương trình. Thêm 3 vào cả hai vế của phương trình

4+ 3 = x – 3 + 3

7 = x

Kiểm tra lời giải bằng cách thay câu trả lời vào phương trình ban đầu.

4 = x – 3

4 = 7 – 3

Do đó x = 7 là đáp án đúng.

Giải phương trình bằng phép trừ

Hãy xem một vài ví dụ dưới đây để hiểu khái niệm này.

Ví dụ 3

Giải cho x trong x + 10 = 16

Giải pháp

x + 10 = 16

Trừ 7 cho cả hai vế của phương trình.

x + 10 – 10 = 16 – 10

x = 6

Ví dụ 4

Giải phương trình tuyến tính 15 = 26 – y

Giải pháp

15 = 26 – y

Trừ 26 cho cả hai vế của phương trình
15 -26 = 26 – 26 -y
– 11 = -y

Nhân cả hai vế với –1

y = 11

Giải phương trình với các biến ở cả hai vế bằng cách cộng

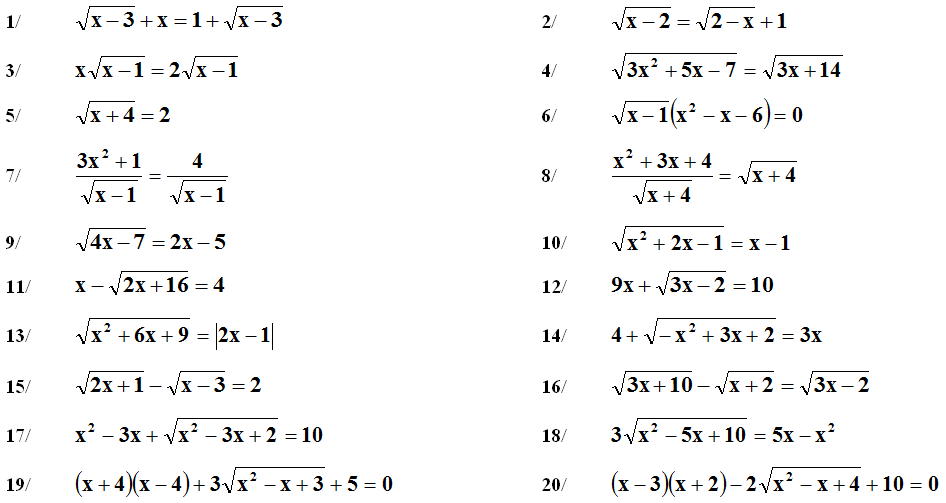
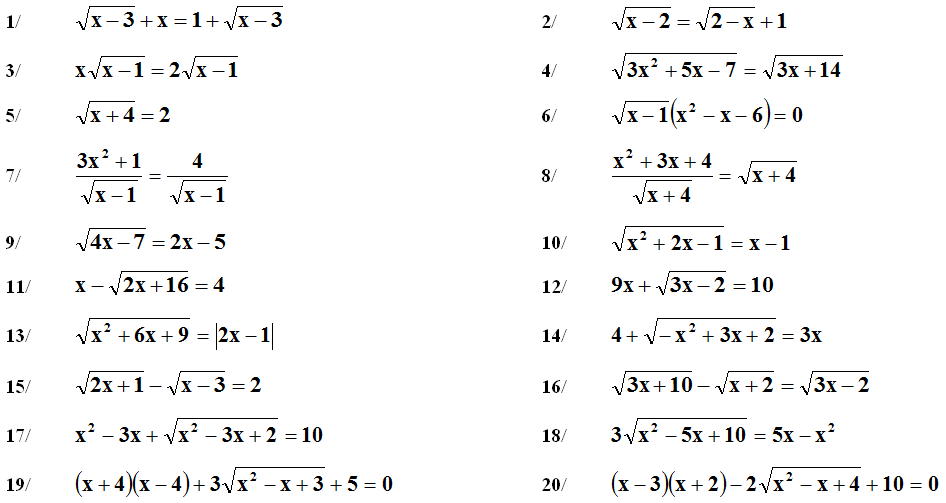
Hãy xem một vài ví dụ dưới đây để hiểu khái niệm này.

Ví dụ 4

Xét phương trình 4x –12 = -x + 8.

Vì một phương trình có hai vế, bạn cần thực hiện cùng một phép toán trên cả hai vế.

Thêm biến x vào cả hai vế của phương trình

⟹ 4x –12 + x = -x + 8 + x.

Đơn giản hóa

Đơn giản hóa phương trình bằng cách thu thập các số hạng tương tự ở cả hai vế của phương trình.

5x – 12 = 8.

Phương trình bây giờ chỉ có một biến ở một phía.

Thêm hằng số 12 vào cả hai vế của phương trình.

Hằng số gắn với biến được thêm vào cả hai bên.

⟹ 5x – 12 +12 = 8 + 12

Đơn giản hóa

Đơn giản hóa phương trình bằng cách kết hợp các số hạng tương tự. và 12.

⟹ 5x = 20

Bây giờ, chia cho hệ số

Chia cả hai vế cho hệ số chỉ đơn giản là chia tất cả cho số kèm theo biến.

Giải pháp của phương trình này là do đó,

x = 4.

Xác minh giải pháp của bạn

Kiểm tra xem lời giải có đúng không bằng cách cắm câu trả lời vào phương trình ban đầu.

4x –12 = -x + 8

⟹ 4 (4) –12 = -4 + 8

4 = 4

Do đó, giải pháp là đúng.

Ví dụ 5

Giải -12x -5 -9 + 4x = 8x – 13x + 15 – 8

Giải pháp

Đơn giản hóa bằng cách kết hợp các thuật ngữ tương tự

-8x-14 = -5x +7

Thêm 5x ở cả hai bên.

-8x + 5x -14 = -5x + 5x + 7

-3w -14 = 7

Bây giờ thêm 14 vào cả hai vế của phương trình.

– 3x – 14 + 14 = 7 + 14

-3x = 21

Chia cả hai vế của phương trình cho -3

-3x / -3 = 21/3

x = 7.

Giải phương trình với các biến trên cả hai vế bằng cách trừ

Hãy xem một vài ví dụ dưới đây để hiểu khái niệm này.

Ví dụ 6

Giải phương trình 12x + 3 = 4x + 15

Giải pháp

Trừ 4x cho mỗi vế của phương trình.

12x-4x + 3 = 4x – 4x + 15

6x + 3 = 15

Trừ hằng số 3 cho cả hai vế.

6x + 3 -3 = 15 – 3

6x = 12

Chia hết cho 6;

6x / 6 = 12/6

x = 2

Ví dụ 7

Giải phương trình 2x – 10 = 4x + 30.

Giải pháp

Trừ 2x cho cả hai vế của phương trình.

2x -2x -10 = 4x – 2x + 23

-10 = 2x + 30

Trừ cả hai vế của phương trình cho hằng số 30.

-10 – 30 = 2x + 30 – 30

– 40 = 2x

Bây giờ chia hết cho 2

-40/2 = 2x / 2

-20 = x

Giải phương trình tuyến tính với phép nhân

Phương trình tuyến tính được giải bằng phép nhân nếu phép chia được sử dụng để viết phương trình. Vì vậy, khi bạn nhận thấy một biến bị chia, bạn có thể sử dụng phép nhân để giải phương trình.

Ví dụ 7

Giải ra x / 4 = 8

Giải pháp

Nhân cả hai vế của phương trình với mẫu số của phân số,

4 (x / 4) = 8 x 4

x = 32

Ví dụ 8

Giải ra -x / 5 = 9

Giải pháp

Nhân cả hai vế với 5.

5 (-x / 5) = 9 x 5

-x = 45

Nhân cả hai vế với -1 để hệ số của biến dương.

x = – 45

Giải phương trình tuyến tính với phép chia

Để giải phương trình tuyến tính bằng phép chia, cả hai vế của phương trình được chia cho hệ số của biến. Hãy cùng xem các ví dụ dưới đây.

Ví dụ 9

Giải ra 2x = 4

Giải pháp

Để giải phương trình này, hãy chia cả hai vế cho hệ số của biến số.

2x / 2 = 4/2

x = 2

Ví dụ 10

Giải phương trình −2x = −8

Giải pháp

Chia cả hai vế của phương trình cho 2.

−2x / 2 = −8/2

−x = – 4

Khi nhân cả hai vế với -1, ta nhận được;

x = 4

Xem thêm:

Giải phương trình hai bước – Kỹ thuật & ví dụ đơn giản nhất

Giải phương trình nhiều bước nhanh chóng dễ hiểu

Làm thế nào để giải các phương trình đại số bằng cách sử dụng tính chất phân phối?

Kỹ thuật giải phương trình – Giải phương trình đại số (Phương trình với thuộc tính phân tán)

Giải phương trình bằng cách sử dụng thuộc tính phân phối yêu cầu nhân một số với biểu thức trong dấu ngoặc đơn. Các thuật ngữ tương tự sau đó được kết hợp và sau đó biến biệt lập.

Ví dụ 11

Giải hệ số 2x – 2 (3x – 2) = 2 (x –2) + 20

Giải pháp

2x – 2 (3x – 2) = 2 (x –2) + 20

Sử dụng thuộc tính phân phối để loại bỏ dấu ngoặc
2x – 6x + 4 = 2x – 4 + 20
– 4x + 4 = 2x + 16

Cộng hoặc trừ ở cả hai bên

–4x + 4 – 4 –2x = 2x + 16 – 4 –2x
–6x = 12
x = –2

Kiểm tra câu trả lời bằng cách cắm lời giải vào phương trình.

2x – 2 (3x – 2) = 2 (x –2) + 20

(2 * –2) – 2 ((3 * –2) –2) = 2 (–2 –2) + 20
12 = 12

Ví dụ 12

Giải cho x trong phương trình -3x – 32 = -2 (5 – 4x)

Giải pháp

Áp dụng thuộc tính phân phối để loại bỏ các dấu ngoặc đơn.

–3x – 32 = – 10 + 8x

Cộng cả hai vế của phương trình với 3x sẽ cho,

-3x + 3x – 32 = – 10 + 8x + 3x

= – 10 + 11x = -32

Cộng cả hai vế của phương trình với 10.

– 10 + 10 + 11x = -32 + 10

11x = -2

Chia toàn bộ phương trình cho 11.

11x / 11 = -22/11

x = -2

Làm thế nào để giải phương trình với phân số?

Đừng hoảng sợ khi bạn nhìn thấy các phân số trong một phương trình đại số. Nếu bạn biết tất cả các quy tắc cộng, trừ, nhân và chia, đó là một miếng bánh dành cho bạn.

Để giải phương trình với phân số, bạn cần biến đổi nó thành một phương trình không có phân số.

Phương pháp này còn được gọi là “ bù trừ phân số ”.

Khi giải phương trình với phân số, các bước sau được thực hiện theo các bước sau:

• Xác định bội chung nhỏ nhất của các mẫu số (LCD) của tất cả các phân số trong một phương trình và nhân với tất cả các phân số trong phương trình.
• Cô lập biến.
• Đơn giản hóa cả hai vế của một phương trình bằng cách áp dụng các phép toán đại số đơn giản.
• Áp dụng tính chất chia hoặc nhân để làm cho hệ số của một biến bằng 1.

Ví dụ 13

Giải (3x + 4) / 5 = (2x – 3) / 3

Giải pháp

Màn hình LCD của 5 và 3 là 15, do đó nhân cả hai
(3x + 4) / 5 = (2x – 3) / 3

{(3x + 4) / 5} 15 = {(2x – 3) / 3} 15

9x +12 = 10x -15

Cô lập biến;

9x -10x = -15-12

-x = -25

x = 25

Ví dụ 14

Giải cho x 3 / 2x + 6/4 = 10/3

Giải pháp

Màn hình LCD của 2x, 4 và 3 là 12x

Nhân từng phân số trong phương trình với màn hình LCD.

(3 / 2x) 12x + (6/4) 12x = (10/3) 12x

=> 18 + 18x = 40x

Cô lập biến

22x = 18

x = 18/22

Đơn giản hóa

x = 11/9

Ví dụ 15

Giải cho x (2 + 2x) / 4 = (1 + 2x) / 8

Giải pháp

LCD = 8

Nhân từng phần với màn hình LCD,

=> 4 + 4x = 1 + 2x

Cô lập x;

2x = -3

x = -1,5

Câu hỏi thực hành

1. Giải x trong các phương trình tuyến tính sau:
2. 10x – 7 = 8x + 13
3. x + 1/2 = 3
4. 0,2x = 0,24
5. 2x – 5 = x + 7
6. 11x + 5 = x + 7
7. Tuổi của Jared gấp 4 lần tuổi con trai. Sau 5 năm, Jared sẽ gấp 3 lần tuổi con trai mình. Tìm tuổi hiện tại của Jared và con trai anh ta.
8. Giá thành của 2 chiếc quần tây và 3 chiếc áo sơ mi là 705.TôifaShTôirtcoStS40 ít hơn một cái quần, Tìm giá tiền của mỗi cái áo và cái quần.
9. Một chiếc thuyền mất 6 giờ khi ngược dòng và 5 giờ khi xuôi dòng sông. Tính vận tốc của ca nô trong nước yên khi vận tốc của sông là 3 km / giờ.
10. Một số có hai chữ số mà tổng các chữ số của nó là 7. Khi đảo các chữ số lại thì số được tạo thành ít hơn số ban đầu là 27. Tìm số.
11. 10000TôiSdTôiStrTôibutedamong150people.TôifthemoneyTôiSeTôitherTôinthedenomTôinatTôionof100 hoặc 50 đô la. Tính số lượng từng mệnh giá tiền.
12. Chiều rộng hình chữ nhật kém chiều dài 3cm. Khi tăng chiều rộng và chiều dài lên 2 thì diện tích hình chữ nhật thay đổi gấp 70 cm ²so với diện tích hình chữ nhật ban đầu. Tính các kích thước của hình chữ nhật ban đầu.
13. Tử số của phân số nhỏ hơn mẫu số 8. Khi mẫu số giảm đi 1 và tử số tăng 17 thì phân số trở thành 3/2. Xác định phân số.
14. Tuổi bố 12 tuổi gấp đôi tuổi con. Sau 8 năm nữa tuổi bố gấp 20 lần tuổi con. Tuổi bố hiện nay là bao nhiêu?