Hàm là gì? Xem xong 5 phút hiểu luôn.

• Nhiều đến một chức năng hoặc chức năng Surjective
• Chức năng Onto hoặc chức năng Bijective

Ngoài ra, chúng ta có các loại hàm khác trong Toán học mà bạn có thể học nhanh chóng tại đây, chẳng hạn như Hàm đồng dạng, Hàm hằng số, Hàm đa thức, v.v. Bây giờ chúng ta hãy tìm hiểu, giải thích ngắn gọn với định nghĩa, biểu diễn và ví dụ của nó.

Định nghĩa về các hàm một-một

Một hàm có nhiều loại, và một trong những hàm phổ biến nhất được sử dụng là hàm một đối một hoặc hàm bị tổn thương. Ngoài ra, chúng ta sẽ học ở đây tính nghịch đảo của hàm này.

Các hàm một-một xác định rằng mỗi phần tử của một tập hợp, chẳng hạn như Tập hợp (A) được ánh xạ với một phần tử duy nhất của tập hợp khác, chẳng hạn như Tập hợp (B).

Hoặc là

Nó  có thể được định nghĩa là mỗi phần tử của Tập hợp A có một phần tử duy nhất trên Tập hợp B.

Hoặc là

Một đơn ánh (tiêm) hoặc chức năng one-to-one là một chức năng mà các bản đồ các yếu tố riêng biệt của phạm vi của nó đến các yếu tố riêng biệt của codomain của nó.

Tóm lại, chúng ta hãy coi ‘f’ là một hàm có miền được đặt là A. Hàm được cho là vô tích nếu với mọi x và y trong A,

Bất cứ khi nào f (x) = f (y), thì x = y

Và tương đương, nếu x ≠ y, thì f (x) ≠ f (y)

Về mặt hình thức, nó được phát biểu là, nếu f (x) = f (y) ngụ ý x = y, thì f là ánh xạ một-một, hoặc f là 1-1 .

Tương tự, nếu “f” là một hàm đối với một, với miền A và phạm vi B, thì nghịch đảo của hàm f được cho bởi;

f ^-1 (y) = x; nếu và chỉ khi f (x) = y

Một hàm f: X → Y được cho là một đối một (hoặc hàm không xác định), nếu ảnh của các phần tử phân biệt của X dưới f là phân biệt, tức là, với mọi x ₁ , x ₂ ∈ X, f (x ₁ ) = f (x ₂ ) ngụ ý x ₁   = x ₂ . Nếu không, nó được gọi là nhiều đối với một hàm.

Hình dưới đây cho thấy hai hàm, trong đó (i) là hàm phân tích (một đối một) và (ii) không phải là hàm phân tích, tức là hàm nhiều một.

Trong Toán học, một hàm tổng hợp hoặc một hàm hoặc một hàm là một hàm bao gồm tính riêng lẻ mà không bao giờ ánh xạ các phần tử rời rạc của miền của nó với phần tử tương đương của miền đồng của nó. Có thể nói, mọi phần tử của miền đồng là hình ảnh của duy nhất một phần tử trong miền của nó.

Các ví dụ

Ví dụ về chức năng chủ quan

• Hàm đồng nhất X → X luôn là hàm vô vi.
• Nếu hàm f: R → R thì f (x) = 2x là hàm vô vi.
• Nếu hàm f: R → R thì f (x) = 2x + 1 là hàm vô vi.
• Nếu hàm f: R → R thì f (x) = x ² không phải là hàm vi phân, vì ở đây nếu x = -1 thì f (-1) = 1 = f (1). Do đó, phần tử codomain không rời rạc ở đây.
• Nếu hàm f: R → R thì f (x) = x / 2 là hàm vô vi.
• Nếu hàm f: R → R thì f (x) = x ³ là vi phân.
• Nếu hàm f: R → R thì f (x) = 4x + 5 là vi phân.

Đồ thị một đối một – Kiểm tra đường ngang

Một chức năng bị tổn thương có thể được xác định bằng phép thử đường ngang hoặc phép thử hình học.

1. Nếu một đường ngang cắt đồ thị của hàm nhiều hơn một lần, thì hàm không được ánh xạ dưới dạng một đối một.
2. Nếu một đường nằm ngang chỉ có thể cắt đồ thị của hàm một lần duy nhất, thì hàm được ánh xạ dưới dạng một đối một.

Xét đồ thị của hàm số (x) = sin x hoặc cos x như hình bên dưới.

Đối với đồ thị này, khi chúng ta vẽ đường thẳng nằm ngang, nó cắt đồ thị sin x hoặc cos x tại nhiều hơn một điểm. Vì vậy, các chức năng này không phải là một chức năng.

Hình dưới đây cho thấy các ví dụ về các hàm một-một khi các hàm này thỏa mãn phép thử đường ngang.

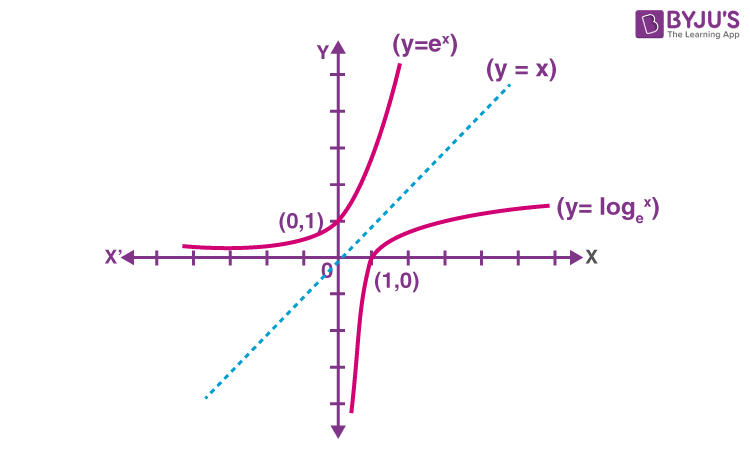
Parabol có phải là một hàm một không?

Không, một parabol không phải là một hàm 1-1. Nó có thể được chứng minh bằng phép thử đường ngang.

Một parabol được biểu diễn bởi hàm f (x) = x ²

Bây giờ, nếu chúng ta vẽ các đường nằm ngang, thì nó sẽ cắt parabol tại hai điểm trong đồ thị. Do đó, với mỗi giá trị của x, sẽ có hai đầu ra cho một đầu vào duy nhất.

Nghịch đảo một với một hàm

Nếu f là hàm xác định y = f (x) thì hàm nghịch biến của f là x = f ^-1 (y) tức là f ^-1 xác định từ y đến x. Trong hàm ngược, miền đồng biến của f là miền của f ^-1 và miền của f là miền đồng biến của f ^-1 .

Chỉ các hàm một đối một mới có khả năng nghịch đảo của nó vì các hàm này có tương ứng từ một đến một, tức là mỗi phần tử trong phạm vi tương ứng với một và chỉ một phần tử miền.

Cho một hàm f: A -> B xác định, thì f được cho là khả nghịch nếu tồn tại một hàm g: B -> A theo cách sao cho nếu chúng ta hoạt động f {g (x)} hoặc g {f ( x)} chúng ta nhận được điểm bắt đầu hoặc giá trị.

Hãy cho chúng tôi hiểu với sự trợ giúp của một ví dụ,

Thí dụ:

Chứng tỏ rằng hàm f: X -> Y, sao cho f (x) = 5x + 7,

Với mọi x, y ∈ N khả nghịch.

Giải pháp: 

Cho y ∈ N -> y = f (x) = 5x + 7 với x ∈ N

x = (y-7) / 5

Nếu chúng ta định nghĩa h: Y -> X theo h (y) = (y-7) / 5

Lại h ∘ f (x) = h [f (x)] = h {5x + 7} = 5 (y-7) / 5 + 7 = x

Và f ∘ h (y) = f [h (y)] = f ((y-7) / 5) = 5 (y-7) / 5 + 7 = y

Do đó f là hàm khả nghịch và h là hàm ngược của f.

Thuộc tính của một chức năng

• Nếu f và g là một đối một, thì f ∘ g tuân theo tính vi phân.
• Nếu g ∘ f là 1-1 thì hàm f là 1-1, nhưng hàm g có thể không.
• f: X → Y là một, nếu và chỉ khi, cho bất kỳ hàm nào g, h: P → X bất cứ khi nào f ∘ g = f ∘ h, thì g = h. Nói cách khác, các hàm một-một chính xác là các đơn thể trong nhóm danh mục các tập hợp.
• Nếu f: X → Y là một và P là một tập con của X thì f ^-1  (f (A)) = P. Do đó, P có thể được lấy ra từ ảnh f (P) của nó.
• Nếu f: X → Y là một và P và Q đều là tập con của X thì f (P ∩ Q) = f (P) ∩ f (Q).
• Nếu cả X và Y đều bị giới hạn với cùng số phần tử, thì f: X → Y là một, nếu và chỉ khi f là hàm xạ ảnh hoặc hàm.

Các vấn đề đã được giải quyết

Ví dụ 1:

Cho A = {1, 2, 3} và B = {a, b, c, d}. Hàm nào sau đây là hàm một đối một?

1. {(1, c), (2, c) (2, c)}
2. {(1, a), (2, b), (3, c)}
3. {(1, b) (1, c)}

Câu trả lời là 2.

Giải thích: Ở đây, phương án số 2 thỏa mãn điều kiện một đối một, vì các phần tử của tập B (phạm vi) là duy nhất mappe d với các phần tử của tập A (miền).

Ví dụ 2:

Chứng tỏ rằng f: R → R xác định khi f (a) = 3a ³  – 4 là một hàm một?

Giải pháp:

Đặt f (a ₁ ) = f (a ₂ ) với mọi a ₁ , a ₂  ∈ R

nên 3a ₁ ³  – 4 = 3a ₂ ³  – 4

a ₁ ³  = a ₂ ³

a ₁ ³  – a ₂ ³  = 0

(a ₁  – a ₂ ) (a ₁  + a ₁ a ₂  + a ₂ ² ) = 0

a ₁  = a ₂ và (a ₁ ²  + a ₁ a ₂  + a ₂ ² ) = 0

(a ₁ ²  + a ₁ a ₂  + a ₂ ² ) = 0 không được xét vì không có giá trị thực  của a ₁  và a ₂ .

Do đó, hàm f đã cho là một.

Học sinh được khuyên giải nhiều hơn các vấn đề ví dụ như vậy, để hiểu khái niệm ánh xạ một-một một cách rõ ràng. Để tìm hiểu thêm về các khái niệm Toán học khác nhau, hãy đăng ký với BYJU’S. Ngoài ra, hãy tải xuống ứng dụng của nó để nhận các video học tập được cá nhân hóa.