Contents
Hệ thống số trong Toán học là gì?
Hệ thống số được định nghĩa là một hệ thống chữ viết để biểu thị các số. Nó là ký hiệu toán học để biểu diễn các số của một tập hợp nhất định bằng cách sử dụng các chữ số hoặc các ký hiệu khác một cách nhất quán. Nó cung cấp một biểu diễn duy nhất của mọi số và đại diện cho cấu trúc số học và đại số của các hình. Nó cũng cho phép chúng ta vận hành các phép toán số học như cộng, trừ và chia.
Giá trị của bất kỳ chữ số nào trong một số có thể được xác định bằng:
- Chữ số
- Vị trí của nó trong số
- Cơ sở của hệ thống số
Số là gì?
Số là một giá trị toán học được sử dụng để đếm hoặc đo lường hoặc ghi nhãn các đối tượng. Các con số được sử dụng để thực hiện các phép tính số học. Ví dụ về số là số tự nhiên, số nguyên, số hữu tỉ và số vô tỉ,… 0 cũng là số biểu thị giá trị rỗng.
Một số có nhiều biến thể khác như số chẵn và lẻ, số nguyên tố và hợp số. Các số hạng chẵn và lẻ được sử dụng khi một số chia hết cho 2 hoặc không, trong khi số nguyên tố và hợp số phân biệt giữa các số chỉ có hai thừa số và nhiều hơn hai thừa số, tương ứng.
Trong một hệ thống số, những số này được sử dụng dưới dạng chữ số. 0 và 1 là các chữ số phổ biến nhất trong hệ thống số, được sử dụng để biểu diễn các số nhị phân. Mặt khác, các chữ số từ 0 đến 9 cũng được sử dụng cho các hệ thống số khác. Hãy cùng chúng tôi tìm hiểu ở đây các loại hệ thống số.
Các loại hệ thống số
Có nhiều loại hệ thống số trong toán học. Bốn loại hệ thống số phổ biến nhất là:
- Hệ thống số thập phân (Cơ số- 10)
- Hệ thống số nhị phân (Cơ số 2)
- Hệ thống số bát phân (Cơ số 8)
- Hệ thống số thập lục phân (Cơ số- 16)
Hệ thống số thập phân (Hệ thống số cơ sở 10)
Hệ thống số thập phân có cơ số 10 vì nó sử dụng mười chữ số từ 0 đến 9. Trong hệ thống số thập phân, các vị trí kế tiếp bên trái của dấu thập phân đại diện cho đơn vị, hàng chục, hàng trăm, hàng nghìn, v.v. Hệ thống này được thể hiện bằng số thập phân .
Mỗi vị trí cho thấy một sức mạnh cụ thể của cơ sở (10). Ví dụ: số thập phân 1457 bao gồm chữ số 7 ở vị trí hàng đơn vị, 5 ở vị trí hàng chục, 4 ở vị trí hàng trăm và 1 ở vị trí hàng nghìn mà giá trị có thể được viết là
(1 × 10 3 ) + (4 × 10 2 ) + (5 × 10 1 ) + (7 × 10 0 )
(1 × 1000) + (4 × 100) + (5 × 10) + (7 × 1)
1000 + 400 + 50 + 7
1457
Hệ thống số nhị phân (Hệ thống số cơ sở 2)
Hệ thống số cơ số 2 còn được gọi là hệ thống số nhị phân , trong đó chỉ có hai chữ số nhị phân tồn tại, tức là 0 và 1. Cụ thể, cơ số 2 thông thường là cơ số của 2. Các số liệu được mô tả trong hệ thống này được gọi là hệ nhị phân các số là sự kết hợp của 0 và 1. Ví dụ: 110101 là một số nhị phân.
Chúng ta có thể chuyển đổi bất kỳ hệ thống nào thành hệ nhị phân và ngược lại.
Thí dụ
Viết (14) 10 dưới dạng số nhị phân.
Giải pháp:


Ví dụ về hệ thống số cơ sở 2
∴ (14) 10 = 1110 2
Hệ thống số bát phân (Hệ thống số cơ sở 8)
Trong hệ thống số bát phân , cơ số là 8 và nó sử dụng các số từ 0 đến 7 để biểu diễn các số. Số bát phân thường được sử dụng trong các ứng dụng máy tính. Chuyển đổi một số bát phân sang thập phân cũng giống như chuyển đổi số thập phân và được giải thích bên dưới bằng cách sử dụng một ví dụ.
Ví dụ: Chuyển 215 8 thành số thập phân.
Giải pháp:
215 8 = 2 × 8 2 + 1 × 8 1 + 5 × 8 0
= 2 × 64 + 1 × 8 + 5 × 1
= 128 + 8 + 5
= 141 10
Hệ thống số thập lục phân (Hệ thống số 16 cơ sở)
Trong hệ thập lục phân, các số được viết hoặc biểu diễn với cơ số 16. Trong hệ thập lục phân, đầu tiên các số được biểu diễn giống như trong hệ thập phân, tức là từ 0 đến 9. Sau đó, các số được biểu diễn bằng các bảng chữ cái từ A đến F. Bảng dưới đây cho thấy sự biểu diễn của các số trong hệ thống số thập lục phân .
| Hệ thập lục phân | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | số 8 | 9 | A | B | C | D | E | F |
| Thập phân | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | số 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
Biểu đồ hệ thống số
Trong biểu đồ hệ thống số, có thể tìm thấy các giá trị cơ bản và các chữ số của hệ thống số khác nhau. Dưới đây là biểu đồ của hệ thống chữ số.
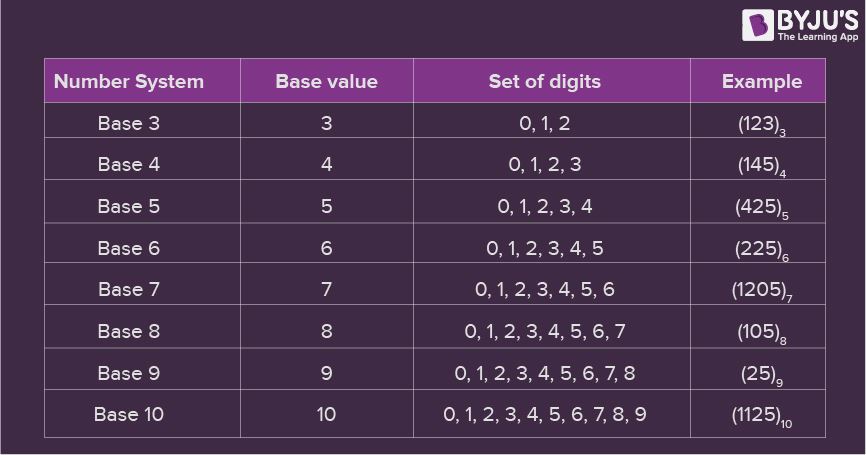

Biểu đồ hệ thống số
Chuyển đổi hệ thống số
Các số có thể được biểu diễn trong bất kỳ danh mục hệ thống số nào như nhị phân, thập phân, thập lục phân, v.v. Ngoài ra, bất kỳ số nào được biểu thị trong bất kỳ loại hệ thống số nào đều có thể dễ dàng chuyển đổi sang loại khác. Kiểm tra bài học chi tiết về chuyển đổi của các hệ thống số để tìm hiểu cách chuyển đổi số từ hệ thập phân sang nhị phân và ngược lại, hệ thập lục phân sang nhị phân và ngược lại, bát phân sang nhị phân và ngược lại bằng các ví dụ khác nhau.
Các ví dụ đã giải quyết
Q.1: Chuyển (1056) 16 thành số bát phân.
Lời giải: Cho, 1056 16 là một số hex.
Đầu tiên chúng ta cần chuyển đổi số thập lục phân đã cho thành số thập phân
(1056) 16
= 1 x 16 3 + 0 x 16 2 + 5 x 16 1 + 6 x 16 0
= 4096 + 0 + 80 + 6
= (4182) 10
Bây giờ chúng ta sẽ chuyển đổi số thập phân này thành số bát phân bắt buộc bằng cách chia lặp lại cho 8.
| số 8 | 4182 | Phần còn lại |
| số 8 | 522 | 6 |
| số 8 | 65 | 2 |
| số 8 | số 8 | 1 |
| số 8 | 1 | 0 |
| 0 | 1 |
Do đó, lấy giá trị của phần dư từ dưới lên trên, ta được;
(4182) 10 = (10126) 8
Vì thế,
(1056) 16 = (10126) 8
Q.2: Chuyển (1001001100) 2 sang số thập phân.
Giải pháp: (1001001100) 2
= 1 x 2 9 + 0 x 2 8 + 0 x 2 7 + 1 x 2 6 + 0 x 2 5 + 0 x 2 4 + 1 x 2 3 + 1 x 2 2 + 0 x 2 1 + 0 x 2 0
= 512 + 64 + 8 + 4
= (588) 10
Q.3: Chuyển 10101 2 thành số bát phân.
Giải pháp: Đưa ra,
10101 2 là số nhị phân
Chúng ta có thể viết số nhị phân đã cho dưới dạng:
010 101
Như chúng ta đã biết, trong hệ thống số bát phân,
010 → 2
101 → 5
Do đó, số bát phân yêu cầu là 25 8
Q.4: Chuyển đổi hệ thập lục phân 2C sang số thập phân.
Giải pháp: Trước tiên chúng ta cần chuyển 2C 16 thành số nhị phân.
2C → 00101100
Bây giờ chuyển 00101100 2 thành một số thập phân.
101100 = 1 × 2 5 + 1 × 2 3 + 1 × 2 2
= 32 + 8 + 4
= 44
Câu hỏi về hệ thống số
- Chuyển (242) 10 thành hệ thập lục phân. [ Trả lời: (F2) 16 ]
- Chuyển 0,52 thành một số bát phân. [ Trả lời: 4121]
- Trừ 1101 2 và 1010 2 . [ Trả lời: 0010]
- Biểu diễn 5C6 dưới dạng số thập phân. [ Trả lời: 1478]
- Biểu diễn số nhị phân 1.1 dưới dạng thập phân. [ Trả lời: 1.5]
Hệ thống số máy tính (Hệ thống số trong máy tính)
Khi chúng ta nhập bất kỳ chữ cái hoặc từ nào, máy tính sẽ dịch chúng thành số vì máy tính chỉ có thể hiểu các con số. Máy tính chỉ có thể hiểu một số ký hiệu được gọi là chữ số và những ký hiệu này mô tả các giá trị khác nhau tùy thuộc vào vị trí mà chúng giữ trong số. Nói chung, hệ thống số nhị phân được sử dụng trong máy tính. Tuy nhiên, hệ thống bát phân, thập phân và thập lục phân cũng được sử dụng đôi khi.
Các câu hỏi thường gặp
Hệ thống số là gì và các loại của nó?
Hệ thống số chỉ đơn giản là một hệ thống để biểu diễn hoặc thể hiện các con số. Có nhiều loại hệ thống số khác nhau và những hệ thống được sử dụng phổ biến nhất là hệ thống số thập phân, hệ thống số nhị phân, hệ thống số bát phân và hệ thống số thập lục phân.
Tại sao hệ thống số lại quan trọng?
Hệ thống số giúp biểu diễn các con số trong một tập hợp ký hiệu nhỏ. Nói chung, máy tính sử dụng các số nhị phân 0 và 1 để giữ cho các phép tính đơn giản và giữ cho số lượng mạch cần thiết ít hơn, dẫn đến ít không gian, tiêu thụ năng lượng và chi phí nhất.
Hệ thống số cơ sở 1 được gọi là gì?
Hệ thống số cơ sở 1 được gọi là hệ thống số một bậc và là hệ thống chữ số đơn giản nhất để biểu diễn các số tự nhiên.