Khoảng cách giữa đường thẳng và mặt phẳng
Trong không gian đường thẳng và mặt phẳng có 3 vị trí tương đối: Cắt nhau; Đường thẳng nằm trên mặt phẳng; Đường thẳng song song với mặt phẳng.
bình thường một bài toán dạng này sẽ không hỏi về 2 trường hợp đường thẳng cắt hoặc nằm trên mặt phẳng. Trong các trường hợp này chúng ta có thể coi khoảng cách giữa đường thẳng và mặt phẳng là bằng 0.
Trong trường hợp đường thẳng d và mặt phẳng (P) song song với nhau. Khoảng cách giữa d và (P) là khoảng cách từ 1 điểm bất cứ trên d tới mặt phẳng (P). Ký hiệu là d(d,(P)).
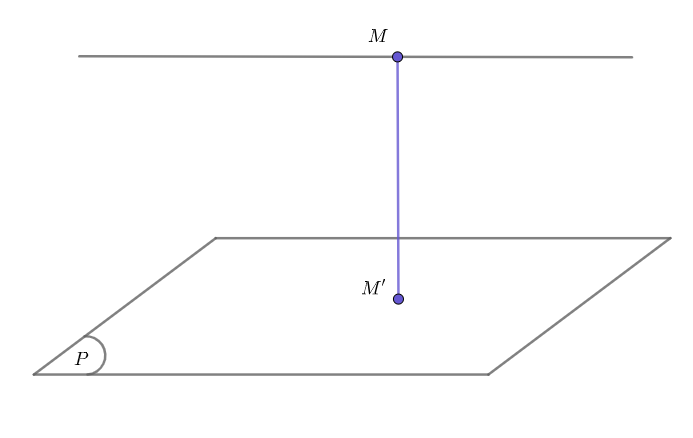

CÔNG THỨC TÍNH KHOẢNG CÁCH GIỮA ĐƯỜNG THẲNG VÀ MẶT PHẲNG đồng thời
Trong không gian Oxyz, cho đường thẳng d và mặt phẳng (P) song song với nhau. Đường thẳng d có chứa điểm M(α;β;γ). Mặt phẳng (P) có phương trình:
ax+by+cz+d=0. Khi đó khoảng cách giữa d và (P) được tính theo công thức:
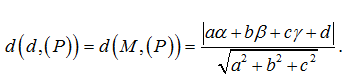
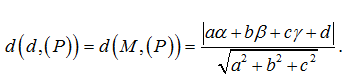
Như vậy khoảng cách giữa đường thẳng và mặt phẳng đồng thời được tính hoàn toàn theo công thức khoảng cách giữa điểm và mặt phẳng. Thậm chí việc lựa chọn điểm còn thỏa mái hơn bởi chúng ta có thể chọn M là bất kỳ điểm nào trên đường thẳng d.
thí dụ minh họa:
Trong không gian Oxyz cho đường thẳng d và mặt phẳng (P) tuần tự có phương trình:
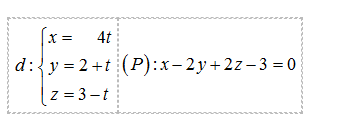
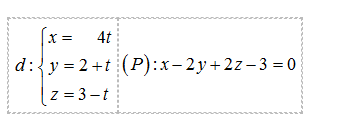
Tính khoảng cách giữa đường thẳng d và mặt phẳng (P).
Lời giải:
Để đánh giá đường thẳng có song song hoặc nằm trên mặt phẳng hay không. Ta lấy tích vô hướng của 1 vecto chỉ phương của đường thẳng và 1 vecto pháp tuyến của mặt phẳng. Nếu kết quả bằng 0 thì đường thẳng đồng thời hoặc nằm trên mặt phẳng.


Và đó là Khoảng cách giữa đường thẳng và mặt phẳng được tintuctuyensinh liệt kê , mong rằng các bạn sẽ có thể lựa chọn nhiều tài liệu hơn nữa