Công thức Vecto chỉ phương
29 Tháng Chín, 2021Vecto chỉ phương của đường thẳng là gì? Vecto chỉ phương trong oxyz như nào? Vecto chỉ phương của 2...
Toán học lớp 10 với nhiều tri thức cần thiết, là nền tảng để học trò ôn thi THPTQG. kiến thức đường parabol là gì, cách lập phương trình parabol cũng như cách thức xác định tọa độ đỉnh parabol là những thắc bận bịu được nhiều người chơi ân cần.
Bài viết dưới đây của tintuctuyensinh sẽ giúp người chơi tổng hợp về chủ đề cách lập phương trình parabol cũng như những nội dung tương tác, cùng mày mò nhé!.
Contents
Cho một điểm F nhất mực và một đường thẳng Δ nhất mực không đi qua F.
Thì đường parabol là tập hợp tất cả các điểm M cách đều F và Δ.
Điểm F được gọi là tiêu điểm của parabol.
Đường thẳng Δ được gọi là đường chuẩn của parabol.
Khoảng cách từ F tới Δ được gọi là thông số tiêu của parabol.
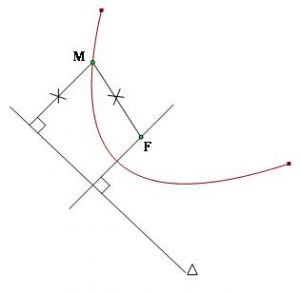

khái niệm đường Parabol
Vậy một đường parabol là một giao hội các điểm trên mặt phẳng cách đều một điểm cho trước (tiêu điểm) và một đường thẳng cho trước (đường chuẩn).
Phương trình Parabol được biểu diễn như sau: y=a2+bx+c
Hoành độ của đỉnh là −b2a
Thay tọa độ trục hoành vào phương trình, ta tìm được hoành độ Parabol có công thức dưới dạng: b2−4ac4a
Phương trình chính tắc của parabol được trình diễn dưới dạng:
y2=2px(p>0)
Chứng minh:
Cho parabol với tiêu điểm F và đường chuẩn Δ.
Kẻ FP⊥Δ(P∈Δ). Đặt FP = p.
Ta chọn hệ trục tọa độ Oxy sao cho O là trung điểm của FP và điểm F nằm trên tia Ox.
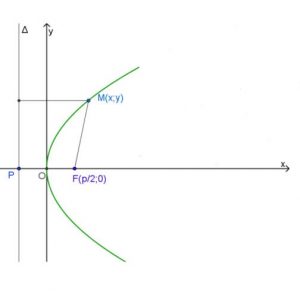

Suy ra ta có F=(P2;0),P=(−P2;0)
Và phương trình của đường thẳng Δ là x+p2=0
Điểm M(x ; y) nằm trên parabol đã cho khi và chỉ khi khoảng cách MF bằng khoảng cách từ M đến Δ, tức là:
(x−p2)2+y2−−−−−−−−−−−√=∣∣x+p2∣∣
Bình phương 2 vế của đẳng thức rồi rút gọn, ta được phương trình chính tắc của parabol:
y2=2px(p>0)
Chú ý: Ở môn đại số, chúng ta gọi đồ thị của hàm số bậc hai y=ax2+bx+c là một đường parabol.
Ví dụ: Xác định tọa độ của đỉnh và các giao điểm với trục tung, trục hoành (nếu có) của mỗi parabol.
a) y=x2–3x+2
b)y=−2×2+4x–3
Hướng dẫn:
a) y=x2–3x+2. Có hệ số: a = 1, b = – 3, c = 2.
Δ=b2–4ac = (-3).2 – 4.1.2 = – 1
Tọa độ đỉnh của đồ thị hàm số I(−b2c;−Δ4a)
Vậy đỉnh parabol là I(−32;−14)
Cho x = 0 → y = 2 ⇒ A(0; 2) là giao điểm của đồ thị hàm số với trục tung.
Cho y = 0 ↔ x2–3x+2=0 ⇔ {x1=1×2=2
Suy ra B(1; 0) và C(2; 0) là giao điểm của đồ thị hàm số với trục hoành.
b) Cho y=−2×2+4x–3. Có a = -2 , b = 4, c = -3
Δ = Δ=b2–4ac = 42 – 4. (-2).(-3) = – 8
Tọa độ đỉnh của đồ thị hàm số I(−b2c;−Δ4a)
Vậy đỉnh parabol là I (1; 1)
Cho x = 0 => y = – 3 ⇒ A(0; -3) là giao điểm của đồ thị hàm số với trục tung.
Cho y = 0 => [latex]-2x^{2} + 4x – 3 = 0\)
Δ = b2 – 4ac = 42 – 4. (-2).(-3) = – 8 ≪ 0.
Phương trình vô nghiệm ⇒ không {sinh tồn|sống sót|tồn tại} giao điểm của hàm số với trục hoành.











Bài viết trên đây đã giúp bạn tổng hợp các tri thức về chủ đề phương trình parabol. hy vọng đã cung ứng cho người học những tri thức có ích đáp ứng cho quá trình nghiên cứu cũng như học tập về phương trình parabol. Chúc người chơi luôn học tốt!.