- Hai cạnh và một góc đối diện
- Một cạnh và hai góc
- Ba cạnh
- Hai mặt và góc giữa chúng
Công thức cho luật tiếp tuyến
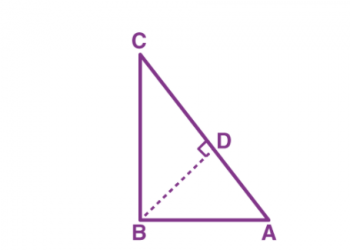
Giả sử một tam giác vuông ABC trong đó các cạnh đối diện với ∠ A , ∠ B , a n d∠ Clần lượt là a, b và c. Khi đó, theo luật tiếp tuyến, chúng ta có ba quan hệ sau:


a – ba + b=rám nắng(A – B2)t a n (A + B2) …. (1)
Tương tự đối với các mặt khác,
b – cb + c=rám nắng(B – C2)t a n (B + C2) … .. (2)
c – ac + a=rám nắng(C– A2)t a n (C+ A2) … .. (3)
Vì tan (- θ) = -tan θ với bất kỳ góc θ nào, chúng ta có thể chuyển đổi thứ tự của các chữ cái trong công thức luật tiếp tuyến ở trên và có thể được viết lại như sau:
b – ab + a=rám nắng(B – A2)t a n (B + A2) ….(4)
Tương tự đối với các mặt khác,
c – bc + b=rám nắng(C– B2)t a n (C+ B2) … .. (5)
a – ca + c=rám nắng(A – C2)t a n (A + C2) … .. (6)
Các công thức (1), (2) và (3) được sử dụng khi a> b, b> c và c> a, và các công thức (4), (5) và (6) được sử dụng khi b> a , c> b và a> c.
Luật chứng minh tiếp tuyến
Để chứng minh: a – ba + b=rám nắng(A – B2)t a n (A + B2)
Chứng minh: Từ định luật sin,
akhông cóA=bkhông cóB=ckhông cóCSử dụng quan hệ thứ nhất và thứ hai,
akhông cóA=bkhông cóB= k , (Nói)
a = k sin A và b = k sin B
Từ đây,
a – b = k (sin A – sin B)
a + b = k (sin A + sin B)
Vì vậy, chúng tôi nhận được
a – ba + b=không cóA – không cóBkhông cóA + không cóB ……… (1)
Công thức Nhận dạng cho Sine là:
không cóA – không cóB = 2 cosA + B2không cóA – B2không cóA + không cóB = 2 sinA + B2cosA – B2Thay các công thức đó vào phương trình (1), ta được
a – ba + b=2 cosA + B2không cóA – B22 tội lỗiA + B2cosA – B2=rám nắngA – B2rám nắngA + B2Do đó đã được chứng minh.
Thực hành vấn đề
Câu hỏi:
Giải tam giác △ A B Ccho trước a = 5, b = 3 và ∠C = 96 ° và tìm giá trị của A – B.
Giải pháp :
Chúng ta biết rằng,
∠A + ∠B + ∠C = 180 °
∠A + ∠B = 180 ° – ∠C = 180 ° – 96 ° = 84 °
Theo luật tiếp tuyến,
cho một tam giác ABC với các cạnh a, b và c tương ứng với các góc A, B và C được cho bởi,
a – ba + b=rám nắng(A – B2)t a n (A + B2)Vì thế,
⇒5 – 35 + 3=rám nắng12( A – B )rám nắng12(84∘) ⇒ rám nắng12( A – B ) =2số 8rám nắng42∘= 0,2251 ⇒12( A – B ) =12,7∘A – B = 25,4 °
Xem thêm: