Lưu ý: Tất cả các hàm đều là quan hệ, nhưng không phải tất cả các quan hệ đều là hàm.


Trong phần này, bạn sẽ tìm thấy những điều cơ bản của chủ đề – định nghĩa hàm và quan hệ, các hàm đặc biệt, các loại quan hệ khác nhau và một số ví dụ đã giải.
Contents
Chức năng là gì?
Một hàm là một quan hệ mô tả rằng chỉ nên có một đầu ra cho mỗi đầu vào (hoặc), chúng ta có thể nói rằng một loại quan hệ đặc biệt (một tập hợp các cặp có thứ tự), tuân theo một quy tắc tức là mọi giá trị X phải được liên kết với chỉ một giá trị y được gọi là một hàm.
Ví dụ:
| Miền | Phạm vi |
| -1 | -3 |
| 1 | 3 |
| 3 | 9 |
Chúng ta cũng hãy xem xét định nghĩa về Miền và Phạm vi của một hàm .
| Miền | Nó là tập hợp các giá trị đầu tiên trong cặp có thứ tự (Tập hợp tất cả các giá trị đầu vào (x)). |
| Phạm vi | Nó là tập hợp các giá trị thứ hai trong cặp có thứ tự (Tập hợp tất cả các giá trị đầu ra (y)). |
Thí dụ:
Trong mối quan hệ, {(-2, 3), {4, 5), (6, -5), (-2, 3)},
Miền là {-2, 4, 6} và phạm vi là {-5, 3, 5}.
Lưu ý : Đừng xem xét các bản sao khi viết miền và phạm vi và cũng nên viết theo thứ tự tăng dần.
Các loại chức năng
Về quan hệ, chúng ta có thể xác định các loại hàm như:
- Một đối một hoặc một hàm Injective: Một hàm f: P → Q được cho là một đối một nếu với mỗi phần tử của P có một phần tử khác biệt của Q.
- Nhiều thành một hàm: Một hàm ánh xạ hai hoặc nhiều phần tử của P với cùng một phần tử của tập Q.
- Chức năng Onto Function hoặc Surjective: Một chức năng mà mọi phần tử của tập hợp Q có hình ảnh trước trong tập hợp P
- Tương ứng một-một hoặc hàm Bijective: Hàm f đối sánh với mỗi phần tử của P với một phần tử rời rạc của Q và mọi phần tử của Q đều có tiền ảnh trong P.
Các hàm đặc biệt trong đại số
Một số chức năng quan trọng như sau:
- Hàm không đổi
- Chức năng nhận dạng
- Hàm tuyến tính
- Hàm giá trị tuyệt đối
- Hàm ngược
Mối quan hệ là gì?
Nó là một tập con của tích Descartes. Hay đơn giản là một loạt các điểm (các cặp có thứ tự). Nói cách khác, quan hệ giữa hai tập hợp được định nghĩa là tập hợp của cặp có thứ tự, trong đó cặp có thứ tự được hình thành bởi đối tượng từ mỗi tập hợp.
Ví dụ: {(-2, 1), (4, 3), (7, -3)}, thường được viết dưới dạng ký hiệu tập hợp với dấu ngoặc nhọn.
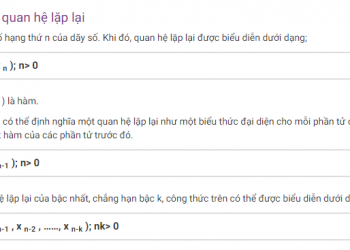
Đại diện quan hệ
Cũng có những cách khác để viết mối quan hệ, ngoài ký hiệu tập hợp chẳng hạn như thông qua bảng, vẽ nó trên trục XY hoặc thông qua sơ đồ ánh xạ.

Các loại quan hệ
Các loại quan hệ khác nhau như sau:
- Quan hệ trống
- Quan hệ toàn cầu
- Mối quan hệ nhận dạng
- Quan hệ nghịch đảo
- Quan hệ phản xạ
- Mối quan hệ đối xứng
- Quan hệ bắc cầu
Hãy để chúng tôi thảo luận về tất cả các loại một.
Mối quan hệ trống rỗng
Khi không có phần tử nào của tập X có liên quan hoặc được ánh xạ với bất kỳ phần tử nào của X, thì quan hệ R trong A là quan hệ rỗng, và còn được gọi là quan hệ rỗng, tức là R = ∅.
Ví dụ, nếu có 100 quả xoài trong giỏ trái cây. Không có khả năng tìm ra mối liên hệ R của việc lấy bất kỳ quả táo nào trong giỏ. Vì vậy, R là Void vì nó có 100 quả xoài và không có quả táo.
Mối quan hệ phổ quát
R là một quan hệ trong một tập hợp, giả sử A là một quan hệ phổ quát vì, trong quan hệ đầy đủ này, mọi phần tử của A đều liên quan đến mọi phần tử của A. tức là R = A × A.
Đó là một quan hệ đầy đủ vì mọi phần tử của Tập hợp A đều nằm trong Tập hợp B.
Mối quan hệ nhân dạng
Nếu mọi phần tử của tập A chỉ liên quan đến chính nó, nó được gọi là quan hệ đồng nhất.
I = {(A, A), ∈ a}.
Ví dụ,
Khi chúng ta ném một con xúc xắc, tổng số kết quả có thể xảy ra là 36. Tức là (1, 1) (1, 2), (1, 3)… .. (6, 6). Từ đó, nếu chúng ta coi quan hệ (1, 1), (2, 2), (3, 3) (4, 4) (5, 5) (6, 6) thì đó là quan hệ đồng nhất.
Mối quan hệ nghịch đảo
Nếu R là một quan hệ từ tập A đến tập B tức là R ∈ AX B. Quan hệ R [latex] ^ {- 1} [/ latex] = {(b, a) 🙁 a, b) ∈ R}.
Ví dụ,
Nếu bạn ném hai con xúc xắc nếu R = {(1, 2) (2, 3)}, R [latex] ^ {- 1} [/ latex] = {(2, 1) (3, 2)}. Ở đây miền là phạm vi R [latex] ^ {- 1} [/ latex] và ngược lại.
Quan hệ phản xạ
Một quan hệ là một quan hệ phản xạ iNếu mọi phần tử của tập A ánh xạ với chính nó, tức là với mọi a ∈ A, (a, a) ∈ R.
Mối quan hệ đối xứng
Quan hệ đối xứng là quan hệ R trên tập A nếu (a, b) ∈ R thì (b, a) ∈ R, với mọi a & b ∈ A.
Quan hệ bắc cầu
Nếu (a, b) ∈ R, (b, c) ∈ R, thì (a, c) ∈ R, với mọi a, b, c ∈ A và quan hệ này trong tập A là bắc cầu.
Quan hệ tương đương
Nếu một quan hệ là phản xạ, đối xứng và bắc cầu thì quan hệ đó được gọi là quan hệ tương đương.
Làm thế nào để chuyển đổi một quan hệ thành một hàm?
Một loại quan hệ đặc biệt (một tập hợp các cặp có thứ tự) tuân theo một quy tắc tức là mọi giá trị X chỉ được liên kết với một giá trị y, khi đó quan hệ được gọi là một hàm.
Các ví dụ
Ví dụ 1 : A = {(1, 5), (1, 5), (3, -8), (3, -8), (3, -8)} có phải là một hàm không?
Giải pháp: Nếu có bất kỳ sự trùng lặp hoặc lặp lại nào trong giá trị X, thì quan hệ đó không phải là một hàm.
Nhưng có một sự thay đổi ở đây. Hãy xem ví dụ sau:


Mặc dù các giá trị X đang được lặp lại ở đây, nhưng nó vẫn là một hàm vì chúng đang liên kết với cùng các giá trị Y.
Điểm (1, 5) được lặp lại ở đây hai lần và (3, -8) được viết ba lần. Chúng ta có thể viết lại nó bằng cách viết một bản sao của các cặp có thứ tự lặp lại. Vì vậy, “A” là một hàm.
Ví dụ 2 : Cho một ví dụ về quan hệ Tương đương.
Giải pháp:
Nếu chúng ta ghi lại tất cả các kết quả của việc ném hai con xúc xắc, nó sẽ bao gồm các quan hệ phản xạ, đối xứng và bắc cầu. Sau đó, ném hai con xúc xắc là một ví dụ về quan hệ tương đương.
Ví dụ 3: Tất cả các hàm đều là quan hệ, nhưng không phải mọi quan hệ đều là hàm. Căn đều.
Giải pháp:
Giả sử, chúng ta có hai quan hệ được cho trong bảng dưới đây
| Một quan hệ không phải là một hàm | Một quan hệ là một hàm |
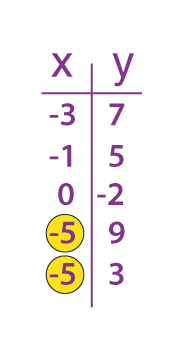 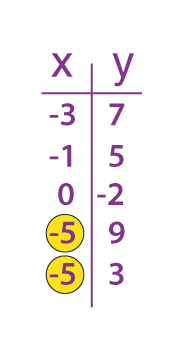 |
  |
| Như chúng ta có thể thấy sự trùng lặp trong các giá trị X với các giá trị y khác nhau, thì mối quan hệ này không phải là một hàm. | Vì mọi giá trị của X đều khác nhau và chỉ được liên kết với một giá trị của y, quan hệ này là một hàm |
Bài học Video
Số chức năng
| Các vấn đề thực hành hàng ngày – BỘ 1 |
| Bảng tính – BỘ 1 |
Các câu hỏi thường gặp về các mối quan hệ và chức năng
Quan hệ có xác định chức năng không?
Một quan hệ từ tập hợp P đến tập hợp Q khác xác định một hàm nếu mỗi phần tử của tập P liên quan đến đúng một phần tử của tập hợp Q.
Quan hệ trong Toán học là gì?
Trong toán học, một quan hệ xác định mối quan hệ giữa các bộ giá trị của các cặp có thứ tự. Tập hợp các phần tử trong tập hợp đầu tiên được gọi là miền có liên quan đến tập hợp phần tử trong tập hợp khác, được gọi là phạm vi.
Làm thế nào để xác định xem một quan hệ có phải là một hàm không?
Khi mỗi giá trị đầu vào của một hàm tạo ra một và duy nhất đầu ra, nó được gọi là một hàm. Ở đây, các giá trị đầu vào được gọi là miền và các giá trị đầu ra được gọi là phạm vi.
Làm thế nào để vẽ đồ thị một hàm số?
Nếu y = x + 2, là một hàm, thì chúng ta phải đặt các giá trị khác nhau của x để tạo ra các giá trị y. Ở đây, x là giá trị đầu vào và y là giá trị đầu ra. Giả sử, nếu x = 0 thì y = 2, nếu x = 1 thì y = 3, nếu x = -1 thì y = 1, v.v. Bây giờ, vẽ các giá trị này trong biểu đồ và nối các điểm.
Xem thêm: