Số mũ là gì? Những thông tin mới nhất về nó
6 Tháng Ba, 2021Lịch sử của lũy thừa hoặc lũy thừa là khá lâu đời. Vào thế kỷ thứ 9 , một nhà toán học người Ba Tư...
Số mũ là lũy thừa hoặc chỉ số. Số mũ hoặc lũy thừa biểu thị số lần một số được nhân nhiều lần với chính nó. Ví dụ, khi chúng ta gặp một số được viết là, 5 3 , nó chỉ đơn giản ngụ ý rằng 5 được nhân với chính nó ba lần. Nói cách khác, 5 3 = 5 x 5 x 5 = 125.
Một biểu thức mũ bao gồm hai phần, đó là cơ số, được ký hiệu là b và số mũ, được ký hiệu là n. Dạng tổng quát của biểu thức mũ là b n .
Contents
Thực hiện phép nhân các số mũ là một phần quan trọng của toán học cấp cao hơn, tuy nhiên nhiều học sinh gặp khó khăn trong việc hiểu cách thực hiện với phép toán này. Mặc dù các biểu thức liên quan đến số mũ âm và nhiều có vẻ khó hiểu.
Trong bài này, chúng ta sẽ học phép nhân số mũ và do đó, điều này sẽ giúp bạn cảm thấy thoải mái hơn khi giải các bài toán với số mũ.
Phép nhân các số mũ dẫn đến các chủ đề con sau:


Trong phép nhân các số mũ có cùng cơ số, các số mũ được cộng với nhau. Quy tắc nhân của phép cộng các số mũ khi các cơ số giống nhau có thể được tổng quát là: a n xa m = a n + m
ví dụ 1
= m 5 + 3
= m⁸
= (-3) 3 +4
= (-3) 7
= 5⁹
= [(-7) × (-7) × (-7) × (-7) × (-7) × (-7) × (-7) × (-7) × (-7) × (-7 )] × [(-7) × (-7) × (-7) × (-7) × (-7) × (-7) × (-7) × (-7) × (-7) × ( -7) × (-7) × (-7)].
= (-7) ²²
Khi nhân hai biến với cơ số khác nhau nhưng cùng số mũ, chúng ta chỉ cần nhân cơ số và đặt cùng một số mũ. Quy tắc này có thể được tóm tắt là:
a n ⋅ b n = (a ⋅ b) n
Ví dụ 2
Nếu cả số mũ và cơ số khác nhau, thì mỗi số được tính riêng và sau đó nhân các kết quả với nhau. Trong trường hợp này, công thức được cho bởi : a n ⋅ b m
Ví dụ 3
Đối với các số có cùng cơ số và số mũ âm, chúng ta chỉ cần thêm các số mũ. Tổng quát: a -n xa -m = a – (n + m) = 1 / a n + m .
Ví dụ 4
Tương tự, nếu các cơ số khác nhau và các số mũ giống nhau, trước tiên chúng ta nhân các cơ số và sử dụng số mũ.
a -n xb -n = (a x b) -n
Ví dụ 5
Khi nhân các phân số cùng cơ số, ta cộng các số mũ. Ví dụ:
(a / b) n x (a / b) m = (a / b) n + m
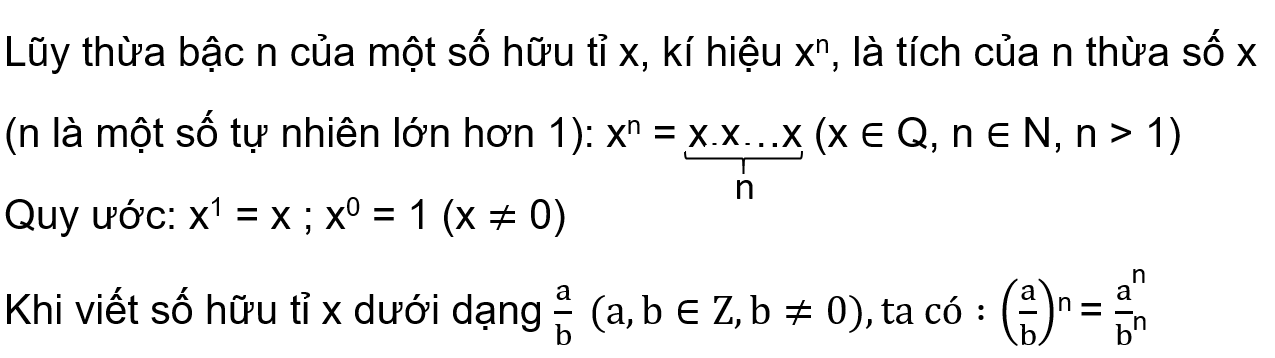
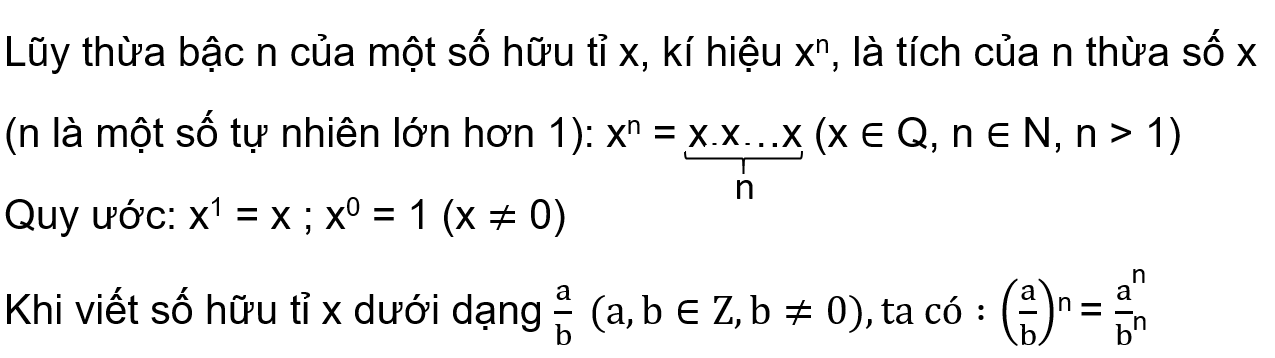
Ví dụ 6
Công thức chung cho trường hợp này là: a n / m ⋅ b n / m = (a ⋅ b) n / m
Ví dụ 7
Tương tự, các số mũ phân số có cùng cơ số nhưng các số mũ khác nhau có công thức tổng quát là: a (n / m) xa (k / j) = a [(n / m) + (k / j)]
Xem thêm:
Hướng dẫn cách trừ các số hỗn hợp chưa đầy 1 phút
Số mũ là gì? Những thông tin mới nhất về nó
Ví dụ 8
Đối với các số mũ có cùng cơ số, chúng ta có thể thêm các số mũ:
(√a) n x (√a) m = a (n + m) / 2
Ví dụ 9
Đối với các số mũ có cùng cơ số, chúng ta có thể thêm các số mũ:
x n * x m = x n + m
Ví dụ 10
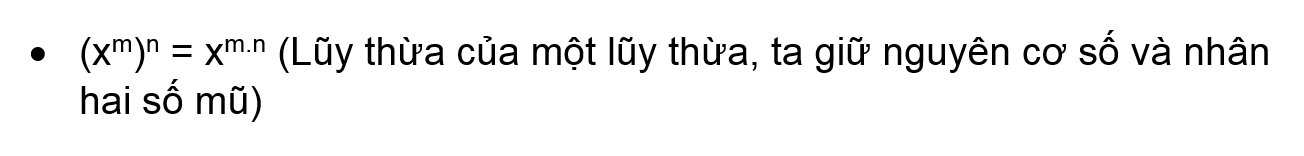
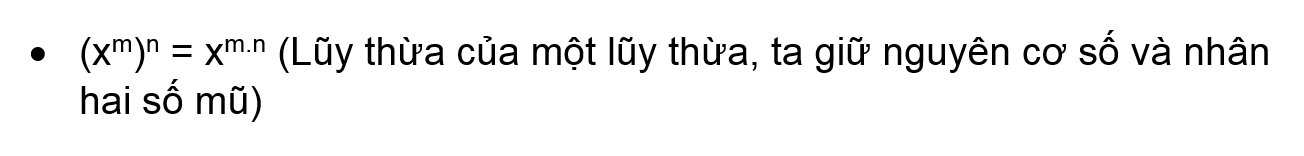
Câu trả lời