Số mũ 0 – Tìm hiểu thông tin liên quan chi tiết nhất

Số mũ là một hàm được biểu diễn dưới dạng x ª, trong đó x biểu thị một hằng số, được gọi là cơ số, và ‘a’, số mũ của hàm này, và có thể là bất kỳ số nào.

Số mũ được gắn vào vai trên bên phải của cơ sở. Nó xác định số lần cơ số được nhân với chính nó. Ví dụ, 4 ³ đại diện cho một phép toán; 4 x 4 x 4 = 64. Mặt khác, lũy thừa phân số biểu thị gốc của cơ số, ví dụ, (81) ^1/2 cho 9.

Quy tắc số mũ bằng không

Xem xét một số cách mà chúng ta có thể xác định một số mũ, chúng ta có thể suy ra quy tắc số mũ bằng không bằng cách xem xét những điều sau:

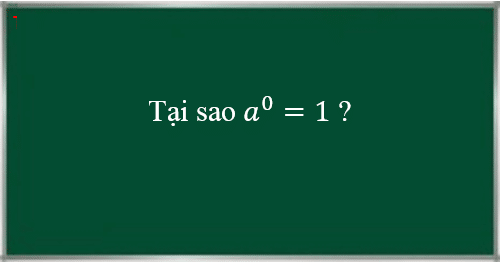
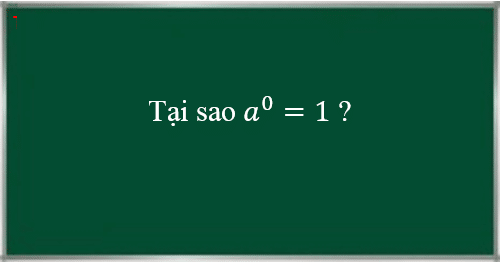
QUẢNG CÁO

• x ²/ x ² = 1. Xét theo quy tắc chia, khi chia các số có cùng cơ số thì chúng ta trừ các số mũ.

x ² / x ² = x ^{2 – 2} = x ⁰ nhưng ta đã biết x ² / x ² = 1; do đó x ⁰ = 1

Do đó, chúng ta có thể kết luận rằng bất kỳ số nào, ngoại trừ số 0 được nâng lên lũy thừa 0 đều là 1.

• Xác minh quy tắc số mũ 0
  Cho số 8 ⁰là một số hạng mũ. Trong trường hợp này, 8 là cơ số và 0 là số mũ.

Nhưng vì chúng ta biết rằng phép nhân của một và bất kỳ số mũ nào cũng tương đương với chính cấp số nhân.

⟹⟹ 8 ⁰ = 1 × 8 ⁰ = 1 × 1

Bây giờ, chúng ta viết số 1 và cơ số 8 bằng 0 lần.

⟹⟹ 8 ⁰ = 1

Do đó, người ta chứng minh rằng bất kỳ số hoặc biểu thức nào được nâng lên thành lũy thừa của 0 luôn bằng 1. Nói cách khác, nếu số mũ bằng 0 thì kết quả là 1. Dạng tổng quát của quy tắc số mũ 0 được cho bởi: a ⁰ = 1 và (a / b) ⁰ = 1.

ví dụ 1

(-3) ⁰ = 1

(2/3) ⁰ = 1

0 ° = không xác định. Điều này tương tự như chia một số cho số không.

Do đó, chúng ta có thể viết quy tắc dưới dạng a ° = 1. Ngoài ra, quy tắc số mũ bằng không có thể được chứng minh bằng cách xem xét các trường hợp sau.

Ví dụ 2
3 ¹  = 3 = 3
3 ²  = 3 * 3 = 9
3 ³  = 3 * 3 * 3 = 27
3 ⁴  = 3 * 3 * 3 * 3 = 81
Và cứ tiếp tục như vậy.

Bạn có thể lưu ý rằng, 3 ³ = (3 ⁴ ) / 3, 3 ² = (3 ³ ) / 3, 3 ¹ = (3 ² ) / 3
3 ^(n-1) = (3 ⁿ ) / 3
Vậy 3 ⁰ = (3 ¹ ) / 3 = 3/3 = 1

Công thức này sẽ hoạt động với bất kỳ số nào nhưng không áp dụng với số 0.

Bây giờ chúng ta hãy tổng quát hóa công thức bằng cách gọi bất kỳ số x:

x ^(n-1) = x ⁿ / x
Vậy x ⁰  = x ^(1-1)  = x ¹ / x = x / x = 1

Và do đó đã được chứng minh.

Ví dụ 3

Hãy xem xét một trường hợp khác của:

5 ²  * 5 ⁴  = 5 ^{(2 + 4)}  = 5 ⁶  = 15625

Trong công thức này, đổi một trong các số mũ thành âm:
5 ²  * 5 ^-4  = 5 ^(2-4)  = 5 ^-2  = 0,04
Điều gì sẽ xảy ra nếu các số mũ có cùng độ lớn:
5 ²  * 5 ^-2  = 5 ^{( 2-2)}  = 5 ⁰

Nhớ lại rằng, một số mũ âm có nghĩa là, một số bị chia cho số mũ:
5 ^-2  = 1/5 ²  = 0,04
Và do đó viết, 5 ²  * 5 ^-2  theo một cách khác:
5 ²  * 5 ^-2  = 5 ²  * 1/5 ²  = 5 ² /5 ²  = 25/25

Vì bất kỳ số nào chia cho chính nó luôn là 1 nên;
5 ²  * 5 ^-2  = 5 ²  * 1/5 ²  = 5 ² /5 ²  = 25/25 = 1
5 ² * 5 ^-2  = 5 ^(2-2)  = 5 ⁰
5 ²  * 5 ^-2  = 5 ² /5 ²  = 1
Điều này ngụ ý rằng 5 ⁰  = 1. Do đó sự cai trị zero-mũ được chứng minh.

Ví dụ 4

Hãy xem xét một trường hợp khác:

x ^a  * x ^b  = x ^{(a + b)}
Nếu ta đổi một trong các số mũ thành âm: x ^a  * x ^-b  = x ^(ab)
Và nếu các số mũ có độ lớn bằng nhau thì x ^a  * x ^-b  = x ^a  * x ^-a  = x ^(aa)  = x ⁰

Bây giờ hãy nhớ lại, một số mũ âm ngụ ý rằng một số bị chia cho số mũ:

x ^-a  = 1 / x ^a
Viết lại x ^a  * x ^-a  theo một cách khác:
x ^a  * x ^-a  = x ^a  * 1 / x ^a  = x ^a / x ^a
Và vì một số bị chia cho chính nó luôn là 1 do đó:
x ^a  * x ^-a  = x ^a * 1 / x ^a  = x ^a / x ^a  = 1:

x ^a  * x ^-a  = x ^(aa)  = x ⁰
và
x ^a  * x ^-a  = x ^a  * 1 / x ^a :

Điều này ngụ ý rằng bất kỳ số nào x ⁰  = 1. Do đó quy tắc số mũ không được chứng minh.

Câu hỏi thực hành

1. Trả lời như sau:
2. (-3) ⁰
3. (-999) ⁰
4. (1/893) ⁰
5. (0,128328) ⁰
6. (√68) ⁰
7. (94/0) ⁰
8. z ⁹/ z ⁹
9. Quần thể vi khuẩn phát triển theo phương trình sau:

p = 150,25 × 10 ^x

với p là dân số và x là số giờ.

Quần thể vi khuẩn ở thời điểm 0 giờ là bao nhiêu?

3. Một số nhân với một số khác có số mũ bằng không. Kết quả là gì?
4. Số đầu tiên.
5. Số thứ hai.
6. 0
7. 1
8. Một số có số mũ là + y thì chia cho cùng số có số mũ là -y. Kết quả là gì?
9. 0
10. 1
11. Nâng số lên lũy thừa 2y.
12. Không có điều nào ở trên.

Câu trả lời

a.1.

b.1

c.1

d.1

e.1

f.

g.1

2. 150,25

3.a

4.c

Xem thêm:

Số mũ là gì? Những thông tin mới nhất về nó

Nhân số mũ như thế nào? Bí quyết nhân nhanh như cao thủ