Số mũ là gì? Những thông tin mới nhất về nó

Lịch sử của lũy thừa hoặc lũy thừa là khá lâu đời. Vào thế kỷ ^thứ 9 , một nhà toán học người Ba Tư Muhammad Musa đã giới thiệu bình phương của một số. Sau đó trong 15 ^ngày thế kỷ, họ đã giới thiệu một khối lập phương của một số. Các ký hiệu đại diện cho các chỉ số này là khác nhau, nhưng phương pháp tính là giống nhau.

Thuật ngữ ‘ mũ ‘ lần đầu tiên được sử dụng trong năm 1544 và thời hạn ‘chỉ số’ lần đầu tiên được sử dụng trong năm 1696. Trong 17 ^ngày thế kỷ, các ký hiệu hàm mũ đã trưởng thành và các nhà toán học khắp nơi trên thế giới bắt đầu sử dụng chúng trong các vấn đề.

Số mũ có nhiều ứng dụng, đặc biệt là trong tăng dân số, phản ứng hóa học, và nhiều lĩnh vực vật lý và sinh học khác. Một trong những ví dụ gần đây về số mũ là xu hướng lây lan của đại dịch Coronavirus (COVID-19), cho thấy sự gia tăng theo cấp số nhân về số lượng người bị nhiễm bệnh.

Số mũ là gì?

Số mũ là lũy thừa hoặc chỉ số. Chúng được sử dụng rộng rãi trong các bài toán đại số, và vì lý do này, điều quan trọng là phải học chúng để giúp việc học đại số trở nên dễ dàng. Trước hết, hãy bắt đầu bằng cách nghiên cứu các phần của một số mũ.

Một biểu thức mũ bao gồm hai phần, đó là cơ số, được ký hiệu là b và số mũ, được ký hiệu là n. Dạng tổng quát của biểu thức mũ là b ⁿ . Ví dụ, 3 x 3 x 3 x 3 có thể được viết dưới dạng cấp số nhân là 3 ⁴ trong đó 3 là cơ số và 4 là số mũ.

Cơ số là thành phần đầu tiên của một cấp số nhân. Cơ số về cơ bản là một số hoặc biến được nhân nhiều lần với chính nó. Trong khi số mũ là phần tử thứ hai được đặt ở góc trên bên phải của cơ số. Số mũ xác định số lần cơ số sẽ được nhân với chính nó.

Luật số mũ

Sau đây là các quy tắc hoặc luật của số mũ:

• Nhân các lũy thừa với một cơ số chung.

Luật ngụ ý rằng nếu các số mũ có cùng cơ số được nhân lên, thì các số mũ sẽ được cộng với nhau. Nói chung:

a ᵐ × a ⁿ = a ^{m + n} và (a / b) ᵐ × (a / b) ⁿ = (a / b) ^{m + n}

Các ví dụ

1. 2³ × 2² = (2 × 2 × 2) × (2 × 2) = 2 ^{3 + 2}= 2 ⁵
2. 5 ³ × 5 ⁶

= (5 × 5 × 5) × (5 × 5 × 5 × 5 × 5 × 5)

= 5 ^{3 + 6}

= 5 ⁹

3. (-7) ¹⁰× (-7) ¹²

= [(-7) × (-7) × (-7) × (-7) × (-7) × (-7) × (-7) × (-7) × (-7) × (-7 )] × [(-7) × (-7) × (-7) ×
(-7) × (-7) × (-7) × (-7) × (-7) × (-7) × ( -7) × (-7) × (-7)]
= (-7) ^{10 + 12}

= (-7) ²²

4. (4/9) ³x (4/9) ²

= (4/9) ^{3 + 2}

= (4/9) ⁵

• Chia số mũ có cùng cơ số

Trong phép chia cấp số nhân cùng cơ số, chúng ta cần thực hiện phép trừ số mũ. Các dạng tổng quát của định luật này là: (a) ^m ÷ (a) ⁿ = a ^{m – n} và (a / b) ^m ÷ (a / b) ⁿ = (a / b) ^m – n

     Các ví dụ

1. 10 ⁵ ÷ 10 ³ = (10) ⁵/ (10) ³

= (10 x 10 x 10 x 10 x 10) / (10 x 10 x 10)

= 10 ^{5 – 3}

= 10 ²

2. (7/2) ⁸÷ (7/2) ⁵

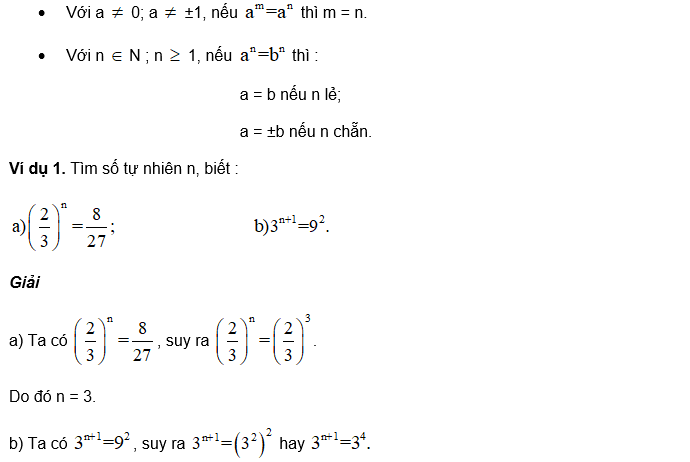
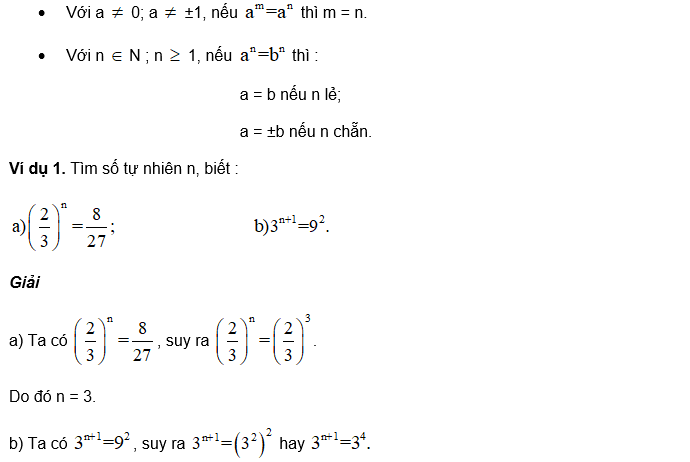
= (7/2) ^{8 – 5}
= (7/2) ³

• Quy luật quyền lực của một quyền lực

Định luật này ngụ ý rằng, chúng ta cần nhân các lũy thừa trong khi một cấp số nhân được nâng lên thành lũy thừa khác. Luật chung là:

(a ^m ) ⁿ = a ^mxn

      Các ví dụ

1. (3 ²) ⁴ = 3 ^{2 x 4}= 3 ⁸
2. {(2/3) ²} ³= (2/3) ^{2 x 3} = (2/3) ⁶

• Quy luật nhân các lũy thừa với các cơ số khác nhau nhưng cùng số mũ.

Dạng tổng quát của quy tắc là: (a) ^m x (b) ^m = (ab) ^m

Các ví dụ

1. 4³ × 2³

= (4 × 4 × 4) × (2 × 2 × 2)

= (4 × 2) × (4 × 2) × (4 × 2)

= 8 × 8 × 8

= 8 ³

2. 2³ × a³

= (2 × 2 × 2) × (a × a × a)

= (2 × a) × (2 × a) × (2 × a)

= (2 × a) ³

= (2a) ³

• Luật số mũ âm

Khi một số mũ là số âm, chúng ta đổi nó thành số dương bằng cách viết 1 ở tử số và số mũ dương ở mẫu số. Các dạng tổng quát của định luật này là: a ^-m = 1 / a ^m a và (a / b) ^-n = (b / a) ⁿ

Các ví dụ

1. 2 ^-2= 1/2 ²= 1/4
2. (2/3) ^-2= (3/2) ²

• Luật số mũ 0

Nếu số mũ bằng 0 thì bạn nhận được kết quả là 1. Dạng tổng quát là: a ⁰ = 1 và (a / b) ⁰ = 1

Các ví dụ

1. (-3) ⁰= 1
2. (2/3) ^{0 =}1

• Số mũ phân số

Trong lũy ​​thừa phân số, công thức tổng quát là: a ^{1 / n} = ⁿ √a trong đó a là cơ số và 1 / n là số mũ. Xem các ví dụ dưới đây.

Các ví dụ

1. 4 ^1/1= 4
2. 4 ^1/2= √4 = 2 (căn bậc nhất của 4)
3. 9 ^1/3= ³√9 = 3 (căn bậc hai của 9)

Câu hỏi thực hành

1. Đơn giản hóa những điều sau đây. Viết câu trả lời cuối cùng dưới dạng số mũ của một số.

1. 2 ^-x× 2 ^x
2. 5 ^-5× 5 ^-3
3. (-7) ²× (-7) ^-99
4. {(10/3) ²} ⁸
5. (5 ^-3) ^-2

1. Quần thể vi khuẩn phát triển theo phương trình sau:

p = 1,25 × 10 ^{x + 1,3}

với p là dân số và x là số giờ.

Dân số vi khuẩn, tính bằng triệu , sau 8 giờ là bao nhiêu?

1. Khối lượng gần đúng của một proton là 1,7 × 10 ^-27 Khối lượng gần đúng của một electron là 9,1 × 10 ^-31 kg. Proton nặng hơn electron bao nhiêu lần?

1. Bất kỳ số nào nâng lên 0 là:

1. 0
2. 1
3. Thông tin là không đủ.

Câu trả lời

1.

1. 1
2. 5 ^-8
3. (-7) ^-97
4. (10/3) ¹⁶
5. 5 ⁶
6. 2494 triệu.
7. 1868
8. B

Xem thêm:

Phương pháp và ví dụ trừ các phân số nhanh chóng nhất

Hướng dẫn cách trừ các số hỗn hợp chưa đầy 1 phút