Contents
Định nghĩa phân phối bình thường
Phân phối Chuẩn được xác định bởi hàm mật độ xác suất cho một biến ngẫu nhiên liên tục trong hệ thống. Giả sử, f (x) là hàm mật độ xác suất và X là biến ngẫu nhiên. Do đó, nó xác định một hàm được tích hợp giữa phạm vi hoặc khoảng (x đến x + dx), cho xác suất của biến ngẫu nhiên X, bằng cách xem xét các giá trị giữa x và x + dx.
f (x) ≥ 0 ∀ x ϵ (−∞, + ∞)
Và -∞ ∫ + ∞ f (x) = 1
Công thức phân phối bình thường
Hàm mật độ xác suất của phân phối chuẩn hoặc gaussian được cho bởi;
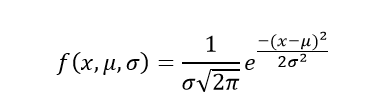
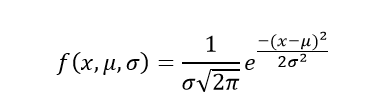
Ở đâu,
- x là biến
- μ là trung bình
- σ là độ lệch chuẩn
Đường cong phân phối bình thường
Các biến ngẫu nhiên tuân theo phân phối chuẩn là những biến có giá trị của nó có thể tìm thấy bất kỳ giá trị nào chưa biết trong một phạm vi nhất định. Ví dụ, tìm chiều cao của học sinh trong trường. Ở đây, phân phối có thể xem xét bất kỳ giá trị nào, nhưng nó sẽ bị giới hạn trong phạm vi, chẳng hạn như 0 đến 6ft. Giới hạn này là bắt buộc về mặt vật lý trong truy vấn của chúng tôi.
Trong khi, phân phối chuẩn thậm chí không bận tâm về phạm vi. Phạm vi cũng có thể mở rộng đến –∞ đến + ∞ và chúng ta vẫn có thể tìm thấy một đường cong mượt mà. Các biến ngẫu nhiên này được gọi là Biến liên tục và Phân phối chuẩn sau đó cung cấp ở đây xác suất của giá trị nằm trong một phạm vi cụ thể cho một thử nghiệm nhất định. Ngoài ra, hãy sử dụng máy tính phân phối chuẩn để tìm hàm mật độ xác suất bằng cách chỉ cung cấp giá trị trung bình và giá trị độ lệch chuẩn.
Độ lệch chuẩn phân phối bình thường
Nói chung, phân phối chuẩn có bất kỳ độ lệch chuẩn dương nào. Chúng ta biết rằng giá trị trung bình giúp xác định đường đối xứng của biểu đồ, trong khi độ lệch chuẩn giúp biết dữ liệu được trải rộng ra sao. Nếu độ lệch chuẩn càng nhỏ, thì dữ liệu có phần gần nhau và biểu đồ trở nên hẹp hơn. Nếu độ lệch chuẩn càng lớn, dữ liệu sẽ bị phân tán nhiều hơn và biểu đồ trở nên rộng hơn. Độ lệch chuẩn được sử dụng để chia nhỏ diện tích dưới đường cong thông thường. Mỗi phần được chia nhỏ xác định tỷ lệ phần trăm dữ liệu, nằm trong vùng cụ thể của biểu đồ.
Sử dụng 1 độ lệch chuẩn, Quy tắc thực nghiệm tuyên bố rằng,
- Khoảng 68% dữ liệu nằm trong một độ lệch chuẩn của giá trị trung bình. (nghĩa là Giữa trung bình- một độ lệch chuẩn và trung bình + một độ lệch chuẩn)
- Khoảng 95% dữ liệu nằm trong hai độ lệch chuẩn của giá trị trung bình. (nghĩa là Giữa trung bình- hai độ lệch chuẩn và trung bình + hai độ lệch chuẩn)
- Khoảng 99,7% dữ liệu nằm trong ba độ lệch chuẩn của giá trị trung bình. (nghĩa là Giữa Trung bình- ba độ lệch chuẩn và Trung bình + ba độ lệch chuẩn)
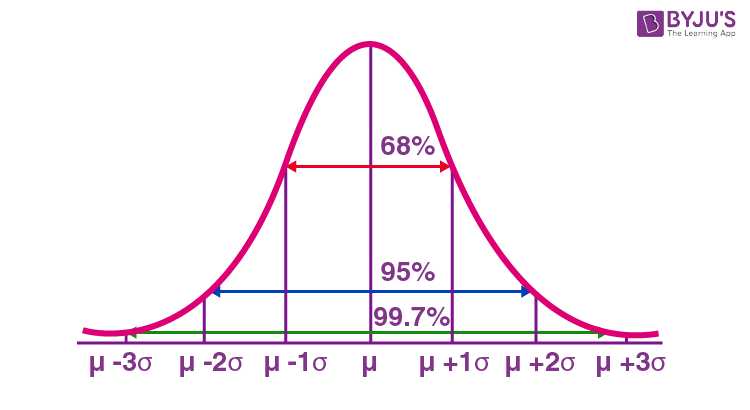

Do đó, quy tắc thực nghiệm còn được gọi là quy tắc 68 – 95 – 99,7 .
Bảng phân phối bình thường
Bảng ở đây hiển thị khu vực từ 0 đến Z-value.
| Giá trị Z | 0,00 | 0,01 | 0,02 | 0,03 | 0,04 | 0,05 | 0,06 | 0,07 | 0,08 | 0,09 |
| 0,0 | 0,0000 | 0,0040 | 0,0080 | 0,0120 | 0,0160 | 0,0199 | 0,0239 | 0,0279 | 0,0319 | 0,0359 |
| 0,1 | 0,0398 | 0,0438 | 0,0478 | 0,0517 | 0,0557 | 0,0596 | 0,0636 | 0,0675 | 0,0714 | 0,0753 |
| 0,2 | 0,0793 | 0,0832 | 0,0871 | 0,0910 | 0,0948 | 0,0987 | 0,1026 | 0,1064 | 0,1103 | 0,1141 |
| 0,3 | 0,1179 | 0,1217 | 0,1255 | 0,1293 | 0,1331 | 0,1368 | 0,1406 | 0,1443 | 0,1480 | 0,1517 |
| 0,4 | 0,1554 | 0,1591 | 0,1628 | 0,1664 | 0,1700 | 0,1736 | 0,1772 | 0,1808 | 0,1844 | 0,1879 |
| 0,5 | 0,1915 | 0,1950 | 0,1985 | 0,2019 | 0,2054 | 0,2088 | 0,2123 | 0,2157 | 0,2190 | 0,2224 |
| 0,6 | 0,2257 | 0,2291 | 0,2324 | 0,2357 | 0,2389 | 0,2422 | 0,2454 | 0,2486 | 0,2517 | 0,2549 |
| 0,7 | 0,2580 | 0,2611 | 0,2642 | 0,2673 | 0,2704 | 0,2734 | 0,2764 | 0,2794 | 0,2823 | 0,2852 |
| 0,8 | 0,2881 | 0,2910 | 0,2939 | 0,2967 | 0,2995 | 0,3023 | 0,3051 | 0,3078 | 0,3106 | 0,3133 |
| 0,9 | 0,3159 | 0,3186 | 0,3212 | 0,3238 | 0,3264 | 0,3289 | 0,3315 | 0,3340 | 0,3365 | 0,3389 |
| 1,0 | 0,3413 | 0,3438 | 0,3461 | 0,3485 | 0,3508 | 0,3531 | 0,3554 | 0,3577 | 0,3599 | 0,3621 |
| 1.1 | 0,3643 | 0,3665 | 0,3686 | 0,3708 | 0,3729 | 0,3749 | 0,3770 | 0,3790 | 0,3810 | 0,3830 |
| 1,2 | 0,3849 | 0,3869 | 0,3888 | 0,3907 | 0,3925 | 0,3944 | 0,3962 | 0,3980 | 0,3997 | 0,4015 |
| 1,3 | 0,4032 | 0,4049 | 0,4066 | 0,4082 | 0,4099 | 0,4115 | 0,4131 | 0,4147 | 0,4162 | 0,4177 |
| 1,4 | 0,4192 | 0,4207 | 0,4222 | 0,4236 | 0,4251 | 0,4265 | 0,4279 | 0,4292 | 0,4306 | 0,4319 |
| 1,5 | 0,4332 | 0,4345 | 0,4357 | 0,4370 | 0,4382 | 0,4394 | 0,4406 | 0,4418 | 0,4429 | 0,4441 |
| 1,6 | 0,4452 | 0,4463 | 0,4474 | 0,4484 | 0,4495 | 0,4505 | 0,4515 | 0,4525 | 0,4535 | 0,4545 |
| 1,7 | 0,4554 | 0,4564 | 0,4573 | 0,4582 | 0,4591 | 0,4599 | 0,4608 | 0,4616 | 0,4625 | 0,4633 |
| 1,8 | 0,4641 | 0,4649 | 0,4656 | 0,4664 | 0,4671 | 0,4678 | 0,4686 | 0,4693 | 0,4699 | 0,4706 |
| 1,9 | 0,4713 | 0,4719 | 0,4726 | 0,4732 | 0,4738 | 0,4744 | 0,4750 | 0,4756 | 0,4761 | 0,4767 |
| 2.0 | 0,4772 | 0,4778 | 0,4783 | 0,4788 | 0,4793 | 0,4798 | 0,4803 | 0,4808 | 0,4812 | 0,4817 |
| 2.1 | 0,4821 | 0,4826 | 0,4830 | 0,4834 | 0,4838 | 0,4842 | 0,4846 | 0,4850 | 0,4854 | 0,4857 |
| 2,2 | 0,4861 | 0,4864 | 0,4868 | 0,4871 | 0,4875 | 0,4878 | 0,4881 | 0,4884 | 0,4887 | 0,4890 |
| 2.3 | 0,4893 | 0,4896 | 0,4898 | 0,4901 | 0,4904 | 0,4906 | 0,4909 | 0,4911 | 0,4913 | 0,4916 |
| 2,4 | 0,4918 | 0,4920 | 0,4922 | 0,4925 | 0,4927 | 0,4929 | 0,4931 | 0,4932 | 0,4934 | 0,4936 |
| 2,5 | 0,4938 | 0,4940 | 0,4941 | 0,4943 | 0,4945 | 0,4946 | 0,4948 | 0,4949 | 0,4951 | 0,4952 |
| 2,6 | 0,4953 | 0,4955 | 0,4956 | 0,4957 | 0,4959 | 0,4960 | 0,4961 | 0,4962 | 0,4963 | 0,4964 |
| 2,7 | 0,4965 | 0,4966 | 0,4967 | 0,4968 | 0,4969 | 0,4970 | 0,4971 | 0,4972 | 0,4973 | 0,4974 |
| 2,8 | 0,4974 | 0,4975 | 0,4976 | 0,4977 | 0,4977 | 0,4978 | 0,4979 | 0,4979 | 0,4980 | 0,4981 |
| 2,9 | 0,4981 | 0,4982 | 0,4982 | 0,4983 | 0,4984 | 0,4984 | 0,4985 | 0,4985 | 0,4986 | 0,4986 |
| 3.0 | 0,4987 | 0,4987 | 0,4987 | 0,4988 | 0,4988 | 0,4989 | 0,4989 | 0,4989 | 0,4990 | 0,4990 |
Các vấn đề và giải pháp phân phối bình thường
Câu 1: Tính hàm mật độ xác suất của phân phối chuẩn bằng cách sử dụng dữ liệu sau. x = 3, μ = 4 và σ = 2.
Lời giải: Cho trước, biến số, x = 3
Mean = 4 và
Độ lệch chuẩn = 2
Bằng công thức mật độ xác suất của phân phối chuẩn, chúng ta có thể viết;
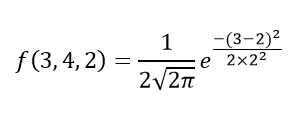
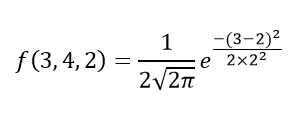
Do đó, f (3,4,2) = 1.106.
Câu hỏi 2: Nếu giá trị của biến ngẫu nhiên là 2, giá trị trung bình là 5 và độ lệch chuẩn là 4 thì hãy tìm hàm mật độ xác suất của phân phối gaussian.
Giải pháp: Đưa ra,
Biến, x = 2
Mean = 5 và
Độ lệch chuẩn = 4
Bằng công thức mật độ xác suất của phân phối chuẩn, chúng ta có thể viết;
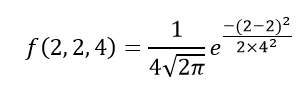
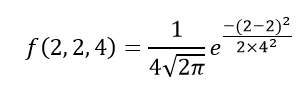
f (2,2,4) = 1 / (4√2π) và 0
f (2,2,4) = 0,0997
Có hai tham số chính của phân phối chuẩn trong thống kê là giá trị trung bình và độ lệch chuẩn. Vị trí và các tham số tỷ lệ của phân phối chuẩn đã cho có thể được ước tính bằng cách sử dụng hai tham số này.
Thuộc tính phân phối bình thường
Một số thuộc tính quan trọng của phân phối chuẩn được liệt kê dưới đây:
- Trong phân phối chuẩn, giá trị trung bình, giá trị trung bình và chế độ bằng nhau. (Nghĩa là Trung bình = Trung vị = Chế độ).
- Tổng diện tích dưới đường cong phải bằng 1.
- Đường cong phân bố chuẩn phải đối xứng ở tâm.
- Phải có chính xác một nửa giá trị ở bên phải tâm và chính xác một nửa giá trị ở bên trái trung tâm.
- Phân phối chuẩn phải được xác định bằng giá trị trung bình và độ lệch chuẩn.
- Đường cong phân phối chuẩn phải chỉ có một đỉnh. (tức là, Unimodal)
- Đường cong tiếp cận trục x, nhưng nó không bao giờ chạm vào và nó mở rộng ra xa giá trị trung bình.
Các ứng dụng
Các phân phối bình thường có liên quan chặt chẽ với nhiều thứ như:
- Điểm đã ghi trong bài kiểm tra
- Chiều cao của những người khác nhau
- Kích thước của các đối tượng do máy sản xuất
- Huyết áp và vân vân.
Câu hỏi thường gặp về phân phối thông thường – Câu hỏi thường gặp
Phân phối chuẩn trong thống kê là gì?
Phân phối chuẩn có nghĩa là gì?
Phân phối chuẩn được sử dụng để làm gì?
Đặc điểm của phân phối chuẩn là gì?
Nó là đối xứng, đơn phương (tức là một chế độ) và tiệm cận.
Các giá trị của giá trị trung bình, giá trị trung bình và chế độ đều bằng nhau.
Một phân phối chuẩn là khá đối xứng về trung tâm của nó. Điều đó có nghĩa là phía bên trái của tâm đỉnh là hình ảnh phản chiếu của phía bên phải. Cũng chỉ có một đỉnh (tức là một chế độ) trong phân phối chuẩn.