Phân số thành số thập phân- Phương pháp chuyển đổi và ví dụ

Phân số thành số thập phân 

Một phân số được tạo thành từ hai phần: tử số và mẫu số. Nó được sử dụng để thể hiện chúng ta có bao nhiêu bộ phận trong tổng số bộ phận.

Chuyển đổi giữa phân số và số thập phân có thể được áp dụng trong cuộc sống hàng ngày của chúng ta khi đo các đại lượng. Một phần thường được sử dụng khi xác định lượng thành phần còn lại trong một gói.

Làm thế nào để chuyển đổi phân số thành số thập phân?

Chuyển phân số thành số thập phân không phải là một nhiệm vụ khó, tuy nhiên để hiểu các phép toán, bạn cần biết về phép chia thập phân. Kỹ năng quan trọng nhất trong chủ đề này cũng là hiểu cách xử lý các số thập phân tận cùng và lặp lại trong câu trả lời cuối cùng.

Trong phân số, tử số là một số nguyên ở trên hoặc trước dấu gạch chéo và mẫu số là một số nguyên sau hoặc dưới dòng. Dòng thường là một ký hiệu phân chia. Do đó, để chuyển một phân số sang số thập phân, tử số được chia cho mẫu số.

Đủ số 0 ở cuối được gắn vào tử số để phép chia tiếp tục tiếp tục cho đến khi kết quả là số thập phân kết thúc hoặc số thập phân lặp lại.

Để chuyển phân số thành số thập phân:

• Chia tử số cho mẫu số. Nếu một phân số là hỗn số, hãy chuyển nó thành một phân số không thích hợp.
• Gắn đủ số 0 ở cuối vào tử số để bạn có thể tiếp tục chia cho đến khi bạn thấy rằng câu trả lời là một số thập phân kết thúc hoặc một số thập phân lặp lại.
• Làm tròn số thập phân nếu phép chia không kết thúc.

ví dụ 1

1. 4/5 dưới dạng phân số được tính là: 4 ÷ 5 = 0,8
2. 75/100 = 75 ÷ 100 = 0,75
3. 3/6 = 3 ÷ 6 = 5.

Chuyển đổi sang số thập phân khi câu trả lời là số thập phân kết thúc

Đôi khi, khi chia tử số của một phân số cho mẫu số, phép chia có kết thúc bằng nhau. Kết quả của kiểu chia này được gọi là số thập phân có tận cùng. Dưới đây là các ví dụ về số thập phân tận cùng.

Ví dụ 2

2/5 = 2,0 ÷ 5

5 chuyển thành 20 bốn lần và dấu thập phân ở cùng một vị trí ở dòng trên cùng.

Do đó, câu trả lời là 0,4.

Ví dụ 3

4/25 = 4,00

4 ÷ 25

25 chuyển thành 40 một lần, để lại 15 như một phần còn lại.

25 chính xác là 150 sáu lần.

Do đó, câu trả lời là 0,16.

Chuyển đổi thành số thập phân khi kết quả là số thập phân định kỳ

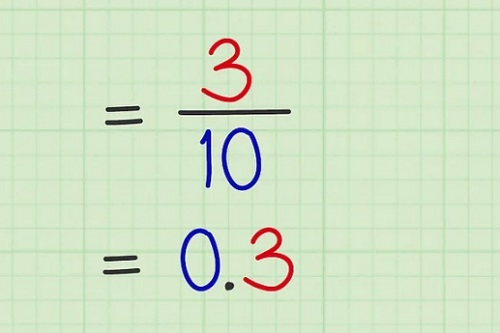
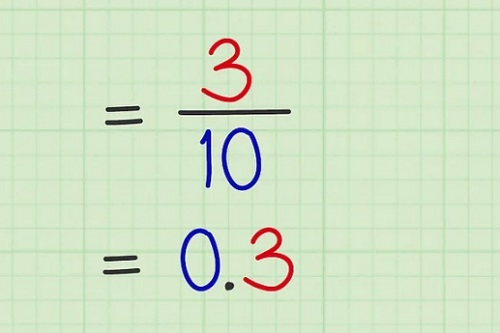
Đôi khi, việc chuyển đổi một phân số dẫn đến một số thập phân lặp lại. Số thập phân lặp lại mãi mãi trong cùng một mẫu số. Ví dụ: để chuyển 2/3 thành số thập phân, hãy bắt đầu bằng cách chia 2 cho 3. Tập luyện bằng cách thêm 3 số không ở cuối và kiểm tra kết quả.

Bạn có thể nhận thấy rằng, phép chia vẫn tiếp tục vô thời hạn cho dù bạn có đính kèm bao nhiêu số 0 ở cuối vào số 2.

Trong trường hợp này 2/3 = 0,666666…, một thanh thường được đặt phía trên số nguyên lặp lại để cho thấy rằng số lặp lại vĩnh viễn.

2/3 = 0,6¯

Có một trường hợp có nhiều hơn một số nguyên lặp lại trong số thập phân liên tiếp hoặc xen kẽ. Ví dụ: giả sử bạn muốn chuyển 5/11 thành phân số thập phân, đây là cách giải quyết vấn đề này:

5/11 = 0,45454545… ..

Người ta nhận thấy rằng mẫu lặp lại mọi số nguyên 4 và 5. Việc thêm nhiều số không ở cuối vào số thập phân ban đầu chỉ chuỗi ra mẫu vô thời hạn. Vì vậy, bạn có thể đại diện là:

5/11 = 0,4¯5

Trong trường hợp này, thanh được đặt phía trên cả số 4 và số 5 để cho thấy rằng hai số này thay thế nhau vô thời hạn.

Chuyển đổi một phân số thành một số thập phân khi Mẫu số là một bội của 10

Khi mẫu số của một phân số là bội số của 10, 100, 1000, 10000, v.v. Sau đó, việc chuyển phân số thành số thập phân là một quá trình đơn giản.

Tử số được viết ra và đặt dấu thập phân bằng cách đếm tổng số các số không từ phải sang trái.

Ví dụ 4

1. 25/100 dưới dạng số thập phân = 0,25
2. 276/1000 = 0,276
3. 8/10 = 0,8

Ví dụ 5

Biểu thị các phân số sau dưới dạng số thập phân:

1. 3/10

Giải pháp

Sử dụng phương pháp trên, chúng ta có

3/10

= 0,3

1. 1479/1000

Giải pháp

1479/1000

= 1.479

1. 71/2

Xem thêm:

Phân chia các số hỗn hợp chỉ trong vài phút tìm hiểu

Hướng dẫn giải phân số phức tạp nhanh chóng nhất

Giải pháp

71/2

= 7 + 1/2

= 7 + (5 × 1) / (5 × 2)

= 7 + 5/10

= 7 + 0,5

= 7,5

1. 91/4

Giải pháp

91/4

= 9 + 1/4

= 9 + (25 × 1) / (25 × 4)

= 9 + 25/100

= 9 + 0,25

= 9,25

1. 121/8

Giải pháp

121/8

= 12 + 1/8

= 12 + (125 × 1) / (125 × 8)

= 12 + 125/1000

= 12 + 0,125

= 12.125