Cách học phép chia đơn giản dễ như trở bàn tay

Phép chia là một trong bốn phép toán cơ bản phân phối một số thành các phần bằng nhau. Nó được biểu thị bằng một số ký hiệu bao gồm, dấu gạch chéo, đường ngang và dấu phân chia. Các đường ngang đã được giới thiệu bởi người Ả Rập và được sử dụng bởi các nhà toán học châu Âu trong 13 ^ngày kỷ. Nó chính thức được sử dụng lần đầu tiên bởi một nhà toán học Thụy Điển, Johann Rahn, vào năm 1659.

Phép chia là gì?

Phép chia là một kỹ thuật toán học trong đó một số được chia thành các nhóm nhỏ hơn hoặc kỹ thuật phân phối các số lượng thành các phần bằng nhau. Đây thường là một trong những phép toán cơ bản trong số học, dẫn đến chia sẻ công bằng.

Phép chia là một phép toán nghịch đảo của phép nhân. Ví dụ, phép nhân 5 với 2 cho 10. Một trong hai thừa số 2 và 5 có thể nhận được bằng cách chia 10 cho bất kỳ số nào.

Các bộ phận của Bộ phận

• Cổ tức

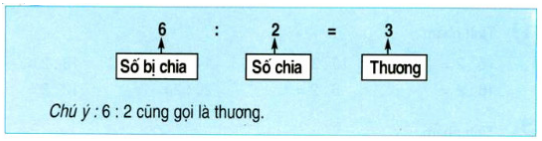
Trong câu chia, số bị chia là số bị chia. Ví dụ, trong một biểu thức: 12 ÷ 3 = 4 ¹ / ₃ , cổ tức là số 12.

• The Divisor

Số bị chia trong câu chia là số chia số bị chia. Ví dụ, trong một phương trình: 12 ÷ 3 = 4 ¹ / _3, số 3 là số chia.

• The Quotient

Thương số là số lần số bị chia chia cho số bị chia. Trong này: 12 ÷ 3 = 4 ¹ / _3, 4 là thương.

• Phần còn lại

Số còn lại sau khi thực hiện phép chia được gọi là phần còn lại. Ví dụ, trong 12 ÷ 3 = 4 ¹ / _3, số 1 là phần còn lại. Có thể lưu ý rằng, số chia là mẫu số của câu trả lời.

Xem thêm:

Ký hiệu mở rộng – Cách để mở rộng số dễ hiểu nhất

Tìm hiểu về dấu lớn hơn trong môn toán học

Thuộc tính của Bộ phận

• Tài sản đóng cửa

Trong phép chia, thuộc tính đóng nói rằng phép chia hai số nguyên không cho thương là một số nguyên. Ví dụ, trong 10 ÷ 5, thương là một số nguyên nhưng đối với 5 ÷ 10, thương không phải là một số nguyên.

• Tính chất giao hoán

Tính chất giao hoán không áp dụng cho phép chia các số. Ví dụ, a ÷ b ≠ b ÷ a.

• Bất động sản kết hợp

Thuộc tính Associative không áp dụng cho phép chia số. Nói chung, a ÷ (b ÷ c) ≠ (a ÷ b) ÷ c

Làm thế nào để chia số?

• Khi một số bị chia cho 1 thì thương chính là số đó.

Ví dụ: 45 ÷ 1 = 45.

• Thương là 1 nếu một số bị chia cho chính nó.

Ví dụ: 5 ÷ 5 = 1

• Trong phép chia bất kỳ số âm hoặc số dương nào cho số 0, kết quả luôn không xác định. Do đó, việc chia bất kỳ số nào cho 0 là vô nghĩa.

Ví dụ: 2 ÷ 0 = Không xác định

• Phép chia số 0 cho bất kỳ số dương hoặc số âm nào, cho số 0 là thương.

Ví dụ: 0 ÷ 2 = 0

• Trong phép chia bất kỳ số nào cho một số khác là bội số của 10, 100, 1000, v.v., dấu thập phân được di chuyển sang trái.

Ví dụ: 5 ÷ 10 = 0,5 và 5 ÷ 1000 = 0,005

• Số dương / Số dương = Thương số dương

Số âm / Số âm = Thương số dương

Số âm / Số dương = Thương số âm

Số dương / Số âm = Thương số âm

Câu hỏi thực hành

1. $ 5,876 được chia cho 26 công nhân. Nếu chia đều số tiền đó thì mỗi người được bao nhiêu tiền?
2. 9975 kg gạo phải đóng 95 bao thì mỗi bao sẽ nặng bao nhiêu kg?
3. 89 người được mời trong một bữa tiệc và một bàn chỉ có thể phục vụ 12 người. Có bao nhiêu bảng là cần thiết trong một phần?
4. Tính số giờ làm được 1200 phút?
5. Một xe buýt có sức chứa 108 hành khách. Nếu xe buýt có 12 hàng ghế. Tính số ghế mỗi hàng trên xe buýt?
6. Một người phụ nữ có 63 quả cam trong một giỏ. Nếu bà chia đều tất cả số cam cho 9 cô con gái của bà. Họ nhận được bao nhiêu cái mỗi cái?
7. Một người bán hàng đã đóng gói 195 chiếc bánh thành 13 gói. Mỗi gói người ấy gói được bao nhiêu cái bánh?
8. Cần 5 quả xoài để làm một ly nước ép xoài. Từ 250 quả xoài có thể làm được bao nhiêu ly nước ép xoài?
9. Một học sinh đếm số tay trong lớp của mình là 120 bàn tay. Có bao nhiêu học sinh được đếm?

Câu trả lời

1. 1. $ 226.
   2. 105 kg
   3. 8 bảng.
   4. 20 giờ
   5. 9 chỗ
   6. 7 quả cam
   7. 15 bánh
   8. 50 ly
   9. 60 học sinh.