Hướng dẫn cách làm phép trừ chuẩn nhất năm 2021

Giống như phép cộng, phép trừ cũng là một trong những phép toán số học lâu đời nhất và cơ bản nhất. Từ trừ có nguồn gốc từ hai từ , ‘ phụ ‘ và ‘ đường ‘ có nghĩa là dưới hoặc dưới và kéo hoặc mang đi tương ứng. Do đó, phép trừ có nghĩa là mang đi phần dưới.

Phép trừ được các nhà toán học biết đến từ hơn 6000 năm trước. Biểu tượng của phép trừ lần đầu tiên được sử dụng bởi các nhà Toán học Đức làm dấu trên thùng, sau đó nó được sử dụng như một biểu tượng hoạt động vào những năm 1500, và sau đó vào năm 1557, nó trở nên phổ biến khi Robert Recorde, một bác sĩ và nhà toán học nổi tiếng, sử dụng nó trong Whetstone của Witte .

Định nghĩa phép trừ

Vào năm 1200, phương pháp trừ được gọi là vay mượn hoặc phân tích. Sau năm 1600, các nhà toán học đưa ra phép trừ số hạng, và được định nghĩa là một phép toán trong đó một số tiền được lấy đi từ tổng số tiền đó. Nó cũng là sự khác biệt giữa hai số tiền.

Phép trừ được ký hiệu bằng dấu gạch ngang (-).

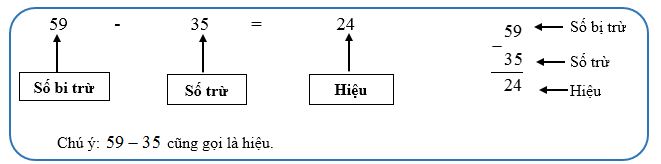
Ví dụ, trong câu trừ 20 – 5 = 15, 5 được lấy đi từ 20, còn lại 15. Câu trừ có bốn phần chính: bội, trừ, một dấu bằng và hiệu.

Việc hiểu các phần của một câu trừ rất hữu ích vì nó cho phép người học nắm được các nguyên tắc chính của phép trừ và phát triển các chiến lược về cách giải quyết các vấn đề về phép trừ.

Các phần của phép trừ

The Minuend

Giá trị nhỏ nhất trong câu trừ là số tiền bắt đầu mà từ đó các số tiền khác được lấy đi. Ví dụ, trong câu trừ: 12 – 8 = 4, giá trị nhỏ nhất là 12.

The Subtrahend

Đây là con số được lấy đi từ số tiền ban đầu. Trong câu trừ: 12 – 8 = 12, phụ là 8. Câu trừ có thể có nhiều bội, tùy thuộc vào mức độ phức tạp của phương trình.

Dấu bằng

Dấu bằng là phần thứ ba của bất kỳ câu trừ nào, nó chỉ ra rằng, hai vế của phương trình là tương đương. Dấu bằng được ký hiệu là ‘ = ‘ và được chèn vào giữa các giá trị bị trừ.

Sự khác biệt

Trong một câu trừ, sự khác biệt là câu trả lời hoặc kết quả của phép toán. Ví dụ, 12 – 8 = 4, sự khác biệt trong trường hợp này là 4.

Thuộc tính của phép trừ

• Thuộc tính nhận dạng

Thuộc tính nhận dạng tuyên bố rằng bất kỳ số nào trừ hoặc cộng với số không đều là chính số đó. Ví dụ,

4 – 0 = 4.

Đối với trường hợp này, nên nhắc nhở người học khi thực hiện phép trừ các nhóm số lớn rằng số 0 không ảnh hưởng đến các số khác trong phương trình.

• Phép toán nghịch đảo

Phép cộng và phép trừ thường đối lập nhau. Ví dụ,

12 + 5 – 5 = 12.

Cộng và trừ cùng một số tiền cũng giống như hủy bỏ hai số tiền. Vì lý do này, học sinh được khuyến khích xác định các số triệt tiêu mỗi số, đặc biệt khi xử lý các phép cộng và trừ các nhóm số lớn.

• Tính chất giao hoán

Tính chất giao hoán nói rằng sự thay đổi vị trí của các số trong một phương trình toán học không ảnh hưởng đến câu trả lời cuối cùng. Tính chất giao hoán không thể áp dụng cho phép trừ vì: 5 – 2 không giống với 2 – 5.

• Bất động sản kết hợp

Thuộc tính kết hợp được áp dụng cho các phương trình sử dụng dấu ngoặc vuông, dấu ngoặc nhọn và dấu ngoặc đơn để nhóm các số lại với nhau. Nói cách khác, bạn có thể di chuyển dấu ngoặc quanh các nhóm khác nhau mà không làm thay đổi câu trả lời cuối cùng.

Tính chất này cũng không thể áp dụng cho phép trừ vì: (3 – 4) – 2 không tương đương với 3 – (4 – 2). Điều này cho thấy rằng bạn không thể di chuyển dấu ngoặc khi làm việc trên một phương trình trừ.

ví dụ 1

Sam có 99 cái bánh nướng nhỏ. Nếu anh ta đưa 32 chiếc cho Nina và 49 chiếc cho Julie, thì anh ta còn lại bao nhiêu chiếc bánh nướng nhỏ?

Giải pháp

Tổng số bánh nướng nhỏ = 99

Nina mất = 32

Julie mất = 49

Số bánh cupcake còn lại = 99 – 32 – 49 = 18

Ví dụ 2

Năm 2012, một công ty có số lượng nhân viên là 1000 nhân viên. Do suy thoái kinh tế, công ty đã cho thôi việc 230 nhân viên vào năm 2015 và 220 nhân viên vào năm 2017. Nếu công ty không thuê thêm nhân viên mới trong giai đoạn này, hãy xác định số lượng nhân viên vào cuối năm 2017.

Giải pháp

Tổng số nhân viên năm 2012 = 1000

Công ty cho thôi việc 230 nhân viên vào năm 2015,

Nhân viên còn lại = 1000 – 230 = 770

Công ty cho thôi việc 220 nhân viên vào năm 2017,

Nhân viên còn lại = 770 – 220 = 550

Xem thêm:

Cách học phép chia đơn giản dễ như trở bàn tay

Phép nhân là gì? Phương pháp học hiệu quả nhất

Ví dụ 3

James, Mike và Curran có tài khoản ngân hàng ở Ngân hàng Trung ương. Mike có500morethanJameSandCurranhave300 ít hơn James. Nếu Mike có $ 1200 trong tài khoản, Curran có bao nhiêu?

Giải pháp

Mike = James + $ 500

Curran = James – 300 đô la

James = Curran + $ 300

Mike = Curran + 300+500

Curran = Mike – 300-500

Curran = Mike – 800 đô la

Curran = 1200-800

Curran = 400 đô la

Câu hỏi thực hành

1. 1. Trong số 568 trẻ em của một làng, có 354 trẻ em được đến trường. Có bao nhiêu trẻ em không đi học?
   2. Một người đã 5680.TôifheSpent3456 trong tổng số tiền, anh ta còn lại bao nhiêu tiền?
   3. Bằng 3689 nhỏ hơn 6789 bao nhiêu?
   4. Melvin kiếm được mức lương hàng tháng là 6777.TôifSheSaveS577 hàng tháng. Tính chi tiêu hàng tháng của cô ấy?
   5. Chi phí của một chiếc điện thoại là 290andthatofawatchTôiS78 ít hơn so với điện thoại. Đồng hồ giá bao nhiêu?
   6. Một phần cứng có 20000 bao xi măng. Nếu đã bán hết 3450 bao thì phần cứng còn lại bao nhiêu bao.
   7. Một người phụ nữ muốn mua một chiếc váy có giá 205,butShehaSonly156. Cô ấy cần thêm bao nhiêu tiền để mua chiếc váy?
   8. Một người đàn ông bắt đầu hành trình ô tô dài 5067 km. Trong tổng hành trình, anh ta đi được 3589 km bằng tàu hỏa và 20 km còn lại đi xe máy. Anh ta đã đi ô tô bao nhiêu km?
   9. Hiệu của hai số là 4509. Nếu số nhỏ hơn là 68888, Tính giá trị của số lớn hơn?
   10. Có 600 học sinh lớp 4 của một trường. Trong tổng số, 200 học sinh có độ tuổi từ 9 đến 11 tuổi và số còn lại có độ tuổi từ 12 đến 13 tuổi. Tính số học sinh có độ tuổi chênh lệch từ 12 đến 13 tuổi?