Số mũ 0 – Tìm hiểu thông tin liên quan chi tiết nhất
6 Tháng Ba, 2021Số mũ là một hàm được biểu diễn dưới dạng x ª, trong đó x biểu thị một hằng...
Contents
Số mũ là lũy thừa hoặc chỉ số. Một biểu thức mũ bao gồm hai phần, đó là cơ số, được ký hiệu là b và số mũ, được ký hiệu là n. Dạng tổng quát của biểu thức mũ là b n . Ví dụ, 3 x 3 x 3 x 3 có thể được viết dưới dạng cấp số nhân là 3 4 trong đó 3 là cơ số và 4 là số mũ. Chúng được sử dụng rộng rãi trong các bài toán đại số, và vì lý do này, điều quan trọng là phải học chúng để làm cho việc học đại số trở nên dễ dàng.
Nhiều học sinh sẽ khó hiểu các số âm và phân số. Nó thường là một thảm họa khi các số mũ âm được thêm vào các phương trình. Chà, không hẳn vậy. Học số mũ âm là nền tảng chính để giải các biểu thức toán học nâng cao. Điều này là do, nó trang bị cho học sinh những kỹ năng và kiến thức cần thiết để đối mặt với những vấn đề khó khăn trong và ngoài lớp học.
Nếu bạn đang băn khoăn không biết bắt đầu từ đâu, đừng lo lắng, bài viết này sẽ giúp bạn chuyển khóa học về số mũ âm thành một trải nghiệm tích cực.
Để giúp bạn hiểu rõ hơn về quy tắc số mũ âm, bài báo này thảo luận chi tiết về các chủ đề sau của quy tắc số mũ âm:
Trước khi giải quyết từng chủ đề này, hãy cùng chúng tôi tóm tắt nhanh các quy tắc của số mũ.

Luật số mũ âm nói rằng, khi một số được nâng lên thành số mũ âm, chúng ta chia 1 cho cơ số được nâng thành số mũ dương. Công thức chung của quy tắc này là: a -m = 1 / a m và (a / b) -n = (b / a) n .
ví dụ 1
Dưới đây là các ví dụ về cách hoạt động của quy tắc số mũ phủ định:


Cơ số b được nâng lên lũy thừa âm của n / m tương đương với 1 chia cho cơ số b được nâng lên thành lũy thừa dương của n / m:
b -n / m = 1 / b n / m = 1 / ( m √b) n
Nó ngụ ý rằng, nếu cơ số 2 được nâng lên số mũ âm của 1/2, thì nó tương đương với số 1 chia cho cơ số 2 được nâng lên số mũ dương của 1/2:
2 -1/2 = 1/2 1/2 = 1 / √ 2 = 0,7071
Bạn nên nhận thấy rằng một số mũ âm phân số cũng giống như việc tìm nghiệm nguyên của cơ số.
Quy tắc ngụ ý rằng, nếu một phân số a / b được nâng lên thành số mũ âm của n, thì nó sẽ bằng 1 chia cho cơ số a / b được nâng thành số mũ dương của n:
(a / b) -n = 1 / (a / b) n = 1 / (a n / b n ) = b n / a n
Cơ số 2/3 nâng lên lũy thừa âm của 2 bằng 1 chia cho cơ số 2/3 nâng lên lũy thừa dương của 2. Nói cách khác, 1 được chia cho nghịch đảo của cơ số được nâng lên thành số mũ dương của 2
(2/3) -2 = 1 / (2/3) 2 = 1 / (2 2 /3 2 ) = (3/2) 2 = 9/4 = 2,25
Khi nhân các số mũ có cùng cơ số, chúng ta có thể cộng các số mũ:
a -n xa -m = a – (n + m ) = 1 / a n + m
Ví dụ 2
2 -3 x 2 -4 = 2 – (3 + 4) = 2 -7 = 1/2 7 = 1 / (2 x 2 x 2 x 2 x 2 x 2 x 2) = 1/128 = 0,0078125
Trong trường hợp các cơ số khác nhau và số mũ chung của a và b, chúng ta có thể nhân a và b:
a -n ⋅ b -n = (a ⋅ b) -n
Ví dụ 3
3 -2 x 4 – 2 = (3 x 4) -2 = 12 -2 = 1/12 2 = 1 / (12 x 12) = 1/144 = 0,0069444
Trong trường hợp cả cơ số và số mũ khác nhau, chúng ta tính riêng từng số mũ rồi nhân:
a -n ⋅ b -m
Ví dụ 4
3 -2 x 4 -3 = (1/9) x (1/64) = 1/576 = 0,0017361
Cách chia số mũ âm
Trong trường hợp các số mũ có cùng cơ số, chúng tôi trừ các số mũ:
a -n / a – m = a -n + m
Xem thêm:
Số mũ 0 – Tìm hiểu thông tin liên quan chi tiết nhất
Cách tính số mũ phân số nhanh chóng nhất hiện nay
Ví dụ 5
2 -6 / 2 -3 = 2 -6 + 3
= 2 -3
= 1/2 3
= 1/8
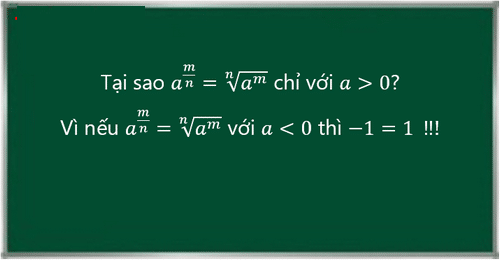
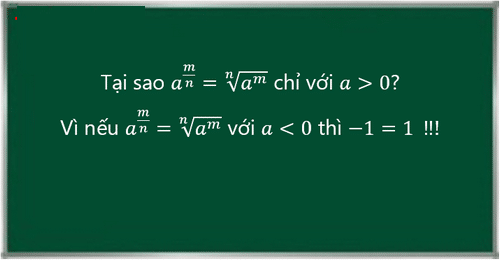
Câu trả lời