Trong toán học, chữ số nhỏ được đặt ở trên và bên phải của bất kỳ số nào được gọi là chỉ số trên. Các số lớn rất khó đọc, khó so sánh và vận hành vì chúng được biểu thị dưới dạng các số nhỏ với sự trợ giúp của các ký tự viết trên. Điều này được thực hiện với sự trợ giúp của quyền hạn và số mũ. Số mũ đại diện cho số lần một số cơ số được nhân lên. Đồng thời, lũy thừa khác với số mũ và bao gồm hai phần được gọi là số cơ số và số mũ.
Contents
Định nghĩa lũy thừa và lũy thừa
Power: Trong Toán học, thuật ngữ ‘lũy thừa’ định nghĩa việc nâng một số cơ bản lên thành số mũ. Nó biểu thị rằng hai yếu tố cơ bản của lũy thừa là “số cơ sở” và “số mũ”. Số cơ sở được định nghĩa là một số được nhân với chính nó, trong khi số mũ đại diện cho số lần số cơ sở được nhân. Tóm lại, lũy thừa là một số được biểu thị bằng số mũ. Nó ngụ ý việc nhân lặp đi lặp lại cùng một hệ số. Một số thuật ngữ đặc biệt được sử dụng trong trường hợp quyền hạn là:
Khi một số là:
- Bình phương – lũy thừa là 2
- cubed – Công suất là 3
- “To the power of” – được sử dụng cho những quyền hạn lớn hơn 3
Số mũ: Trong toán học, số mũ được định nghĩa là một số nhỏ, được đặt ở phía trên bên phải của số cơ sở. Một số mũ có thể là hằng số, số hoặc bất kỳ biến nào. Số mũ biểu thị số cơ số phải được nhân lên bao nhiêu lần. Thông thường, l các số lớn được biểu thị bằng số mũ. Quá trình này được gọi là sự nâng lên thành quyền lực.
Chúng ta có thể thấy các số mũ trong nhiều ký hiệu khoa học để biểu thị các số lớn là lũy thừa của 10. Ví dụ: khoảng cách giữa trái đất và mặt trời được biểu thị dưới dạng số mũ là 1,50 × 10 8 km. Ngoài ra, có một số quy tắc quan trọng trong khi thực hiện một số phép tính số học với số mũ. Họ đang:
- x 0 = 1
- (x m ) n = x mn
- x m × y m = (xy) m
- x m ÷ y m = (x / y) m
- x m × x n = x m + n
- x m ÷ x n = x m-n
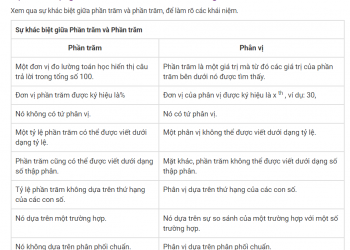
Sự khác nhau giữa lũy thừa và lũy thừa là gì?
| Quyền lực | Số mũ |
| Đề cập đến toàn bộ biểu thức đại diện cho phép nhân lặp lại của cùng một số | Đại diện cho số lần số cơ bản được sử dụng như một hệ số trong việc nhân chính nó |
| Trong , 2 là số cơ bản được nhân với chính nó ba lần và cũng có thể được gọi là “hai với lũy thừa của ba” hoặc “hai với lũy thừa thứ ba”23= 2 × 2 × 2 | Trong , 3 là số mũ đại diện cho số lần 2 được nhân với chính nó23= 2 × 2 × 2 |
Khi các số được biểu diễn dưới dạng số mũ, thì nó được cho là ở dạng cấp số nhân. Từ sự khác biệt giữa lũy thừa và số mũ được cung cấp ở đây, chúng ta có thể nói rằng số mũ là một chữ số nhỏ được đặt ở phía trên bên phải của một số nhất định, trong khi lũy thừa đại diện cho toàn bộ biểu thức, chứa số cơ bản và số mũ.
Các ví dụ đã giải quyết
Q.1: Giải 5 2 .5 3
Giải pháp: Đưa ra,
5 2 .5 3
Sử dụng quy tắc số mũ,
5 2 .5 3 = 5 2 + 3
= 5 5
Q.2: Biểu diễn dưới dạng số mũ.
(i) 2x2x2x2x2
(ii) 3.3.3.3
(iii) 10.10.10
Giải pháp:
(i) 2x2x2x2x2 = 2 5
(ii) 3.3.3.3 = 3 4
(iii) 10.10.10 = 10 3
Q.3: Giải quyết 5 5 /5 2
Lời giải: Theo luật số mũ ta đã biết;
x m / x n = x m-n
Vì thế,
5 5 /5 2
= 5 5-2
= 5 3
Ngoài ra, hãy đọc:
|
Câu hỏi thường gặp – Câu hỏi thường gặp
Lũy thừa và lũy thừa có giống nhau không?
Sự khác biệt giữa công suất và mức độ là gì?
Các quy tắc lũy thừa là gì?
x 0 = 1
(x m ) n = x mn
x m × y m = (xy) m
x m ÷ y m = (x / y) m
x m × x n = x m + n
x m ÷ x n = x m-n
4 nâng lên lũy thừa 3 bằng bao nhiêu?
4 3 = 4 x 4 x 4 = 64