Tìm hiểu về thuộc tính liên kết trong phép nhân cực hay

Thuộc tính liên kết – Giải thích với các ví dụ

Từ ” liên kết ” được lấy từ từ ” liên kết ” có nghĩa là nhóm. Do đó, thuộc tính liên kết có liên quan đến việc phân nhóm. Việc phát hiện ra luật kết hợp đang gây tranh cãi. Nó được giới thiệu bởi không chỉ một người.

Trong những năm đầu 18 ^thứ thế kỷ, các nhà toán học bắt đầu phân tích các loại trừu tượng thứ chứ không phải là con số, và họ muốn nói về các thuộc tính của con số mà giải thích các đối tượng này. Năm 1919, Hamilton sử dụng cụm từ “đặc tính liên quan của hoạt động”.

Tài sản liên kết là gì?

Theo tính chất kết hợp trong toán học, nếu bạn đang cộng hoặc nhân các số, bạn đặt dấu ngoặc ở đâu không quan trọng. Bạn có thể thêm chúng bất cứ nơi nào bạn muốn. Điều này có nghĩa là nhóm các số không quan trọng trong quá trình cộng.

Chỉ có phép cộng và phép nhân là có liên quan, trong khi phép trừ và phép chia là không có tính liên kết.

Bổ sung tài sản

Theo thuộc tính kết hợp của phép cộng, nếu ba hoặc nhiều số được thêm vào, kết quả sẽ giống nhau bất kể cách các số được đặt hoặc nhóm như thế nào.

Giả sử rằng, nếu các số a , b và c được thêm vào và kết quả bằng một số m , thì nếu chúng ta thêm a và b vào trước rồi đến c , hoặc thêm b và c vào trước rồi đến a , thì kết quả vẫn bằng m, tức là

( a + b ) + c = a + ( b + c ) = m

Các số a , b và c được gọi là addend.

Thuộc tính này cũng hoạt động cho nhiều hơn ba số.

ví dụ 1

Chứng tỏ rằng các số sau tuân theo thuộc tính kết hợp của phép cộng:

2, 6 và 9

Giải pháp

2 + 6 + 9

= (2 + 6) + 9 = 8 + 9 = 17

Hoặc là

= 2 + (6 + 9) = 2 + 15 = 17

Kết quả là như nhau trong cả hai trường hợp. Vì thế,

(2 + 6) + 9 = 2 + (6 + 9)

Như một ví dụ thực tế về tài sản liên kết, nếu tôi đi đến quán cà phê và chi tiêu số 8onpTôizza,5 cho kem và 3 đô la cho cà phê, sau đó số tiền tôi nợ người thu ngân có thể được viết dưới dạng tổng tiền là:

(số 8+5) + $ 3

Hoặc là

số 8+(5 + 3 đô la)

Cả hai tổng thành $ 16.

Thuộc tính liên kết của phép nhân

Theo tính chất kết hợp của phép nhân, nếu nhân ba số trở lên, kết quả là như nhau bất kể cách các số được đặt hoặc nhóm như thế nào.

Giả sử rằng, nếu nhân các số a , b và c và kết quả bằng một số n , thì nếu chúng ta nhân a và b trước rồi đến c , hoặc nhân b và c trước rồi đến a , thì kết quả vẫn bằng n , tức là

( a × b ) × c = a × ( b × c ) = n

Thuộc tính này cũng hoạt động cho nhiều hơn ba số.

Các thành phần của hàm và phép nhân ma trận không liên kết với nhau.

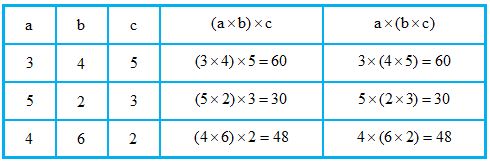
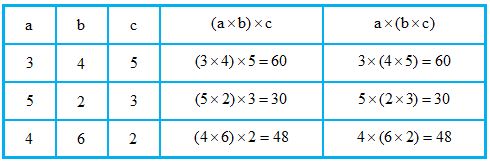
Ví dụ 2

Chứng tỏ rằng các số sau tuân theo thuộc tính kết hợp của phép nhân:

2, 6 và 9

Giải pháp

2 × 6 × 9 = (2 × 6) × 9 = 12 × 9 = 108

2 × 6 × 9 = 2 × (6 × 9) = 2 × 54 = 108

Kết quả là như nhau trong cả hai trường hợp. Vì thế,

(2 × 6) × 9 = 2 × (6 × 9)

Xem thêm:

Thuộc tính danh tính – Giải thích với các ví dụ dễ hiểu nhất

Thuộc tính giao hoán – Những cách giải nhanh gọn nhẹ

Tại sao Phép trừ và Phép chia không liên quan?

Để hiểu tại sao phép trừ và phép chia không tuân theo quy tắc kết hợp, hãy làm theo các ví dụ dưới đây.

Ví dụ 3

Cho biết biểu thức sau có đúng không.

( a – b ) – c = a – ( b – c )

• Bước 1: Những gì bạn cần thể hiện?

( a – b ) – c = a – ( b – c )

• Bước 2: Lấy phía bên trái và cố gắng chứng minh nó bằng với phía bên phải.

( a – b ) – c

• Bước 3: Mở ngoặc đơn.

a – b – c

• Bước 4: Kết hợp b và c trong ngoặc đơn.

a – ( b + c )

• Bước 5: Xem bạn có nhận được kết quả mong muốn hay không.

( a – b ) – c = a – ( b + c )

• Bước 6: Nêu những phát hiện của bạn.

Từ,

( a – b ) – c = a – ( b + c )

Vì thế,

( a – b ) – c ≠ a – ( b – c )

Do đó, biểu thức đã cho là sai và không tuân theo thuộc tính kết hợp.

Ví dụ 4

Cho biết biểu thức sau có đúng không.

(4 a ÷ 2 a ) ÷ a = 4 a ÷ (2 a ÷ a )

• Bước 1: Những gì bạn cần thể hiện?

(4 a ÷ 2 a ) ÷ a = 4 a ÷ (2 a ÷ a )

• Bước 2: Lấy phía bên tay trái.

(4 a ÷ 2 a ) ÷ a

• Bước 3: Giải quyết.

(4 a ÷ 2 a ) ÷ a = (2) ÷ a = 2 / a

• Bước 4: Giải quyết bên tay phải bây giờ.

4 a ÷ (2 a ÷ a ) = 4 a ÷ (2) = 2 a

• Bước 5: Nêu những phát hiện của bạn.

Từ,

(4 a ÷ 2 a ) ÷ a = 2 / a

4 a ÷ (2 a ÷ a ) = 2 a

Vì thế,

(4 a ÷ 2 a ) ÷ a ≠ 4 a ÷ (2 a ÷ a )

Do đó, biểu thức đã cho là sai và không tuân theo thuộc tính kết hợp.