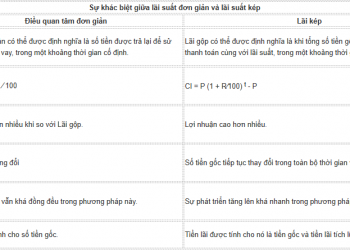
Ví dụ: Tìm diện tích của vùng trong góc phần tư thứ nhất được bao bởi trục x, đường thẳng y = x và đường tròn , x 2 + y 2 = 36
Lời giải: Trước khi tìm diện tích vùng kín, chúng ta cần giải phương trình đã cho của đường cong và đường thẳng, để tìm giao điểm của chúng. Khi giải phương trình x 2 + y 2 = 36 và y = x, ta thấy các giao điểm là (3√2,3√2) và (-3√2, -3√2)
Sau khi tìm được giao điểm, kẻ đường vuông góc từ điểm B đến trục x, tại điểm M.
Tổng vùng được tô bóng là OMABO, có thể được chia thành hai vùng tức là OBMO và BMAB. Đồ thị của đường thẳng và đường cong đã cho có thể được vẽ như hình dưới đây:


Hãy để chúng tôi tìm diện tích của các vùng OBMO và BMAB riêng biệt.
Diện tích OBMO của vùng được cho là:
∫32√0Y. dx =∫32√0x . dx =12(x2)32√0
= 9
Bây giờ chúng ta hãy tìm diện tích của vùng BMAB:
∫632√Y. dx =∫632√36 –x2—–√. dx
= (1236 –x2——√+12× 36 ×không có– 1(x6) )633√
= [½ x 6 x 0 + ½ x 36 x π / 2] – [½ x 3√2 x 3√2 + ½ x 36 x π / 4] = 9π – 9 – 9π / 2 = 9π / 2-9
Bây giờ, thêm các khu vực của hai khu vực mà chúng tôi nhận được,
9 + 9π / 2-9
= 9π / 2 sq.đơn vị.
Lưu ý rằng, trong trường hợp giá trị của diện tích của một số vùng cụ thể là âm, chúng ta cần lấy giá trị tuyệt đối của vùng đó và cộng nó với các vùng còn lại.
Hãy xem xét một ví dụ khác khi chúng ta có một parabol.
Ví dụ: Tìm diện tích vùng giới hạn bởi đường cong y = x 2 và đường thẳng y = 2.
Giải pháp: Đối với trường hợp trên, chúng ta sẽ nhận được hình sau,


Từ hình đã cho, chúng ta có thể thấy rằng parabol là đối xứng qua trục y. Vì vậy, nếu chúng ta tìm thấy vùng kín ở một bên của trục y và nhân đôi nó lên, chúng ta sẽ có diện tích của vùng hoàn chỉnh. Do đó, đối với trường hợp này, chúng ta cần xem xét các dải nằm ngang, bắt đầu từ y = 0 đến y = 2.
Do đó, phương trình cho diện tích sẽ là,
2 x (diện tích của vùng ONBO, được giới hạn bởi đường cong, trục y và các đường y = 0 và y = 2)
2∫20x . dY= 2∫20Y√dY= 2 ×23(Y3 / 2)20
= =273 sq.units
Theo cách tương tự, chúng ta có thể tìm vùng kín trong trường hợp hình elip .
Xem thêm: