Tính thể tích của một hình trụ dễ dàng chỉ trong 1 nốt nhạc

Thể tích của một hình trụ là đơn vị đo thể tích chiếm chỗ của một hình trụ hay còn gọi là thước đo dung tích của một hình trụ.

Trong bài viết này, bạn sẽ học cách tìm thể tích của một hình trụ bằng cách sử dụng công thức thể tích hình trụ.

Trong hình học, hình trụ là một hình 3 chiều có hai đường tròn bằng nhau và song song được nối với nhau bằng một mặt cong.

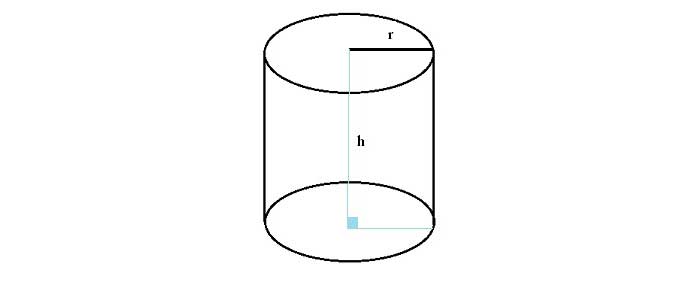
Khoảng cách các mặt tròn của hình trụ được gọi là chiều cao của hình trụ . Đỉnh và đáy của một hình trụ là hai hình tròn đồng dạng có bán kính hoặc đường kính lần lượt là ‘ r ‘ và ‘ d ‘.

Làm thế nào để Tìm thể tích của một xi lanh?

Để tính thể tích của một hình trụ, bạn cần bán kính hoặc đường kính của đáy hoặc đỉnh hình tròn và chiều cao của hình trụ.

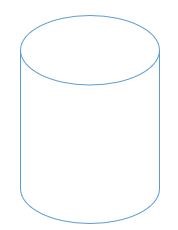
Thể tích của một hình trụ bằng tích giữa diện tích của đáy hình tròn và chiều cao của hình trụ. Thể tích của một hình trụ được đo bằng đơn vị khối.

Tính thể tích của hình trụ rất hữu ích khi thiết kế các vật thể hình trụ như:

• Bể chứa nước hình trụ hoặc giếng
• Cống
• Chai nước hoa hoặc hóa chất
• Hộp đựng và ống hình trụ
• Bình hình trụ dùng trong phòng thí nghiệm hóa học

Công thức thể tích xi lanh

Công thức về thể tích của một hình trụ được cho là:

Thể tích của một hình trụ = πr ² h đơn vị khối

Trong đó, πr ² = diện tích hình tròn;

π = 3,14;

r = bán kính của đáy hình tròn và;

h = chiều cao của hình trụ.

Đối với một hình trụ rỗng, công thức thể tích được cho là:

Thể tích của hình trụ = πh (r ₁ ²  – r ₂ ² )

Trong đó, r ₁  = bán kính ngoài và r ₂ = bán kính trong của hình trụ.

Sự khác biệt của bán kính bên ngoài và bên trong hình thành độ dày thành của một hình trụ tức là

Chiều dày thành của hình trụ = r ₁ – r ₂

Hãy giải một vài bài toán ví dụ về thể tích của hình trụ

ví dụ 1

Đường kính và chiều cao của một hình trụ lần lượt là 28 cm và 10 cm. Thể tích của khối trụ là bao nhiêu?

Giải pháp

Được;

Bán kính bằng một nửa đường kính.

Đường kính = 28 cm ⇒ bán kính = 28/2

= 14 cm

Chiều cao = 10 cm

Bằng công thức thể tích khối trụ;

khối lượng = πr ² giờ

= 3,14 x 14 x 14 x 10

= 6154,4 cm ³

Vậy thể tích của khối trụ là 6154,4 cm ³

Ví dụ 2

Độ sâu của nước trong bể hình trụ là 8 feet. Nếu bán kính và chiều cao của bể lần lượt là 5 feet và 11,5 feet. Tìm thể tích nước cần thiết để đổ đầy bể đến vành.

Giải pháp

Trước hết hãy tính thể tích của cái bể hình trụ

Thể tích = 3,14 x 5 x 5 x 11,5

= 902,75 feet khối

Thể tích nước trong bể = 3,14 x 5 x 5 x 8

= 628 feet khối.

Thể tích nước cần để đổ đầy bể = 902,75 – 628 feet khối

= 274,75 feet khối.

Ví dụ 3

Thể tích của hình trụ là 440 m ³ và bán kính của đáy là 2 m. Tính chiều cao của bể.

Giải pháp

Thể tích của một hình trụ = πr ² h

440 m ³ = 3,14 x 2 x 2 xh

440 = 12,56 giờ

Bằng cách chia 12,56 cho cả hai bên, chúng ta nhận được

h = 35

Do đó, chiều cao của bể là 35 mét.

Ví dụ 4

Bán kính và chiều cao của một bể nước hình trụ lần lượt là 10 cm và 14 cm. Tìm thể tích của bể theo lít.

Giải pháp

Thể tích của một hình trụ = πr ² h

= 3,14 x 10 x 10 x 14

= 4396 cm ³

Cho trước, 1 Lít = 1000 cm khối (cm ³ )

Do đó, hãy chia 4396 cho 1000 để được

Thể tích = 4,396 lít

Ví dụ 5

Bán kính ngoài của ống nhựa là 240 mm và bán kính trong là 200 mm. Nếu chiều dài của ống là 100 mm, hãy tìm khối lượng vật liệu được dùng để làm ống.

Giải pháp

Một đường ống là một ví dụ về hình trụ rỗng, vì vậy chúng ta có

Thể tích của hình trụ = πh (r ₁ ²  – r ₂ ² )

= 3,14 x 100 x (240 ² – 200 ² )

= 3,14 x 100 x 17600

= 5.5264 x 10 ⁶ mm ³ .

Ví dụ 6

Một khối kim loại rắn hình trụ được nung chảy để tạo thành các hình lập phương có cạnh 20 mm. Nếu bán kính và chiều dài của khối trụ lần lượt là 100 mm và 490 mm. Tìm số hình lập phương được tạo thành.

Giải pháp

Tính thể tích của khối trụ

khối lượng = 3,14 x 100 x 100 x 490

= 1.5386 x 10 ⁷ mm ³

Thể tích của khối lập phương = 20 x 20 x 20

= 8000 mm ³

Số khối = thể tích khối trụ / thể tích khối lập phương

= 1.5386 x 10 ⁷ mm ³ /8000 mm ³

= 1923 hình khối.

Ví dụ 7

Tìm bán kính của một hình trụ sẽ có cùng chiều cao và thể tích với một hình lập phương có cạnh 4 ft.

Giải pháp

Được:

Chiều cao của khối lập phương = chiều cao của hình trụ = 4 feet và,

thể tích của khối lập phương = thể tích của khối trụ

4 x 4 x 4 = 64 feet khối

Nhưng thể tích của một hình trụ = πr ² h

3,14 xr ² x 4 = 64 feet khối

12,56r ² = 64

Chia cả hai bên cho 12,56

r ² = 5,1 bộ.

r = 1,72

Do đó, bán kính của hình trụ sẽ là 1,72 feet.

Ví dụ 8

Một hình lăng trụ lục giác đều có chiều dài đáy là 5 cm và chiều cao là 12 cm. Tìm chiều cao của một hình trụ sẽ có cùng thể tích với hình lăng trụ. Lấy bán kính của hình trụ là 5 cm.

Xem thêm:

Hướng dẫn tính thể tích của Kim tự tháp mới nhất 2021

Thể tích của Lăng kính hình chữ nhật và cách giải nhanh nhất