Cách giải tỷ lệ phần trăm của một con số

Tỷ lệ phần trăm của một con số – Giải thích & Ví dụ

Các thuật ngữ phần trăm và phần trăm được sử dụng thay thế cho nhau trong nhiều trường hợp, nhưng chúng có nghĩa giống nhau không?

Chà, phần trăm và phần trăm hơi khác nhau trong cách sử dụng của chúng nhưng chúng có ý nghĩa tương tự. Phần trăm hoặc dấu (%) thường được sử dụng kèm theo một giá trị số. Ví dụ, chúng ta có thể nói, 95 phần trăm hoặc 95% học sinh sáng sủa. Mặt khác, phần trăm thường được sử dụng không có số để chỉ từ phần trăm. Ví dụ, chúng tôi nói rằng, tỷ lệ học sinh sáng sủa là 95%.

Thuật ngữ tỷ lệ phần trăm không quá cũ nhưng phương pháp này đã phổ biến. Khi chưa có hệ thập phân, người La Mã cổ đại thường thực hiện các phép tính phân số dưới dạng bội số của 1/100. Ví dụ, họ đánh thuế hàng hóa theo tỷ lệ 1/100, tương đương với tỷ lệ phần trăm tính toán. Sau đó vào thời Trung cổ, việc sử dụng phân số 1/100 trở nên phổ biến hơn.

Trong 17 ^ngày thế kỷ, một tiêu chuẩn đã được thiết lập để lãi suất quote như 1/100. Sau khi sử dụng thường xuyên của nó, các nhà toán học viết tắt nó là “máy tính” trong 14 ^ngày kỷ. Sau đó là thuật ngữ “per”, và cuối cùng vào năm 1925, DE Smith đã cho nó một dạng ký hiệu (%).

Phần trăm của một số là gì?

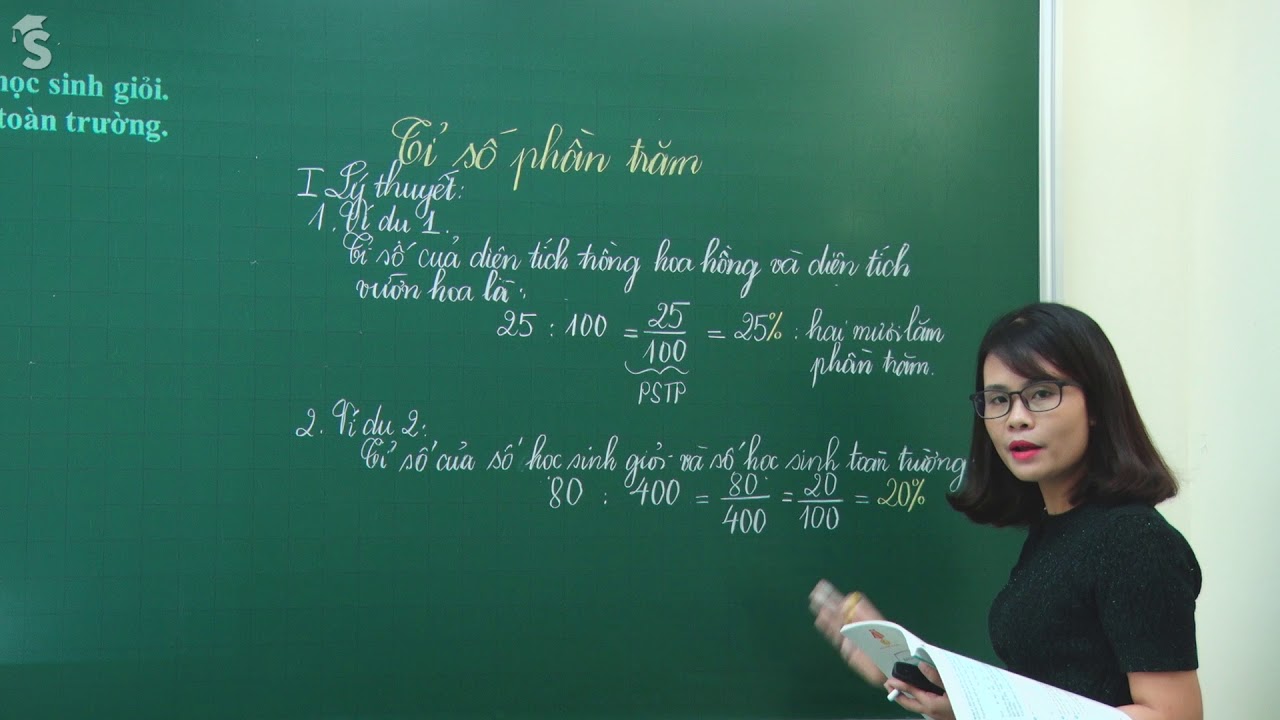
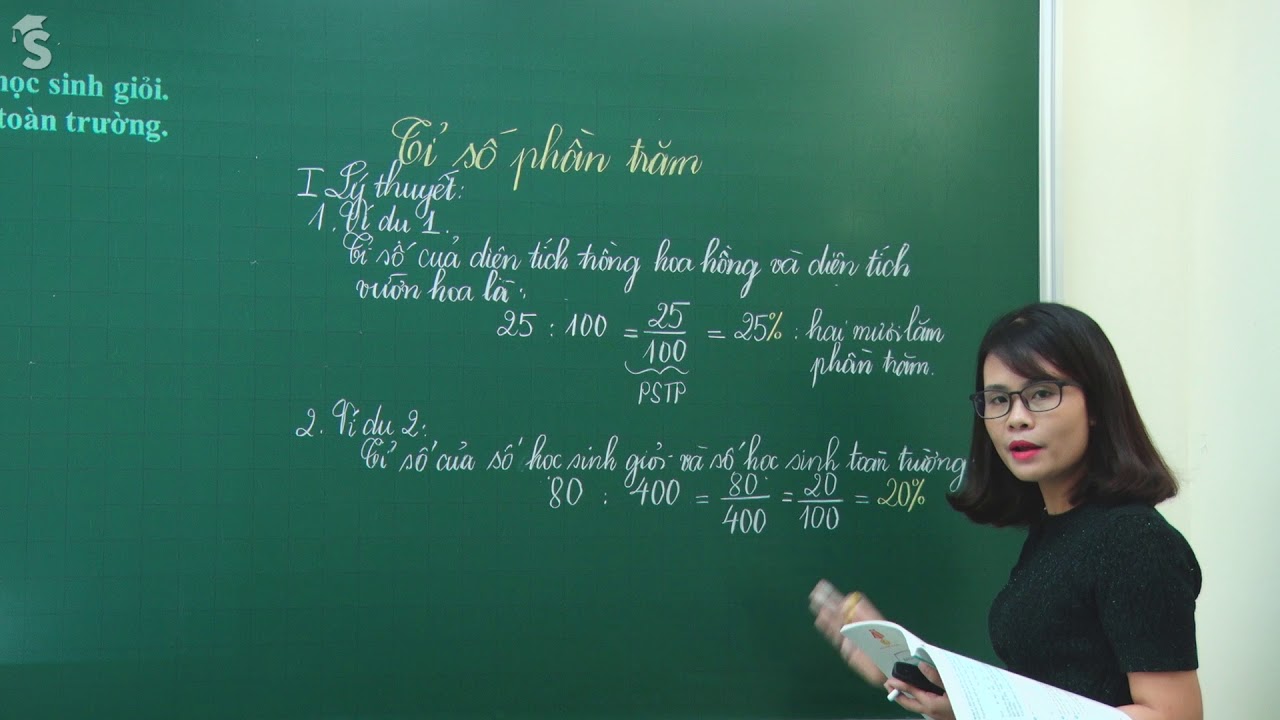
Phần trăm trong toán học là một số hoặc tỷ lệ có thể được biểu diễn dưới dạng phân số của 100. Thuật ngữ phần trăm bắt nguồn từ một từ tiếng Latinh ‘per centum’ có nghĩa là trên 100. Ký hiệu (%) được sử dụng để biểu thị phần trăm.

Tương tự, tỷ lệ phần trăm đôi khi được biểu thị bằng chữ viết tắt ‘pct.’ Ví dụ: chúng ta có thể biểu thị 50 phần trăm là 50% hoặc 50 phần trăm. Phần trăm được viết cho biết số nguyên, phân số hoặc số thập phân. Ví dụ, 4%, 75%, 0,6%, 0,25%, 3/5%, v.v. đều là tỷ lệ phần trăm.

Tỷ lệ phần trăm là một phần của cuộc sống hàng ngày của chúng ta trong các ví dụ sau:

• Giảm giá hàng hóa được thể hiện theo tỷ lệ phần trăm
• Các tổ chức tài chính như ngân hàng và SACCOS biểu thị lãi suất đối với các khoản vay dưới dạng tỷ lệ phần trăm.
• Lãi và lỗ được tính theo tỷ lệ phần trăm
• Trong học thuật, tỷ lệ phần trăm được sử dụng để đánh giá kết quả hoạt động của học sinh
• Giá trị của những chiếc xe hơi và một mảnh đất thay đổi theo thời gian. Điều này có thể được đại diện cho thông báo về tỷ lệ phần trăm.

Vì những lý do này, việc sở hữu kiến ​​thức về cách tính tỷ lệ phần trăm không chỉ giúp bạn trở nên xuất sắc trong toán học mà còn có thể áp dụng bên ngoài lớp học và giải quyết các vấn đề thực tế liên quan đến tỷ lệ phần trăm. Bài viết này cung cấp hướng dẫn từng bước về cách tính tỷ lệ phần trăm.

Làm thế nào để tính toán phần trăm?

Có hai khả năng tìm phần trăm của một số:

• Để tìm phần trăm của một số khi nó ở dạng thập phân, bạn chỉ cần nhân số thập phân với 100. Ví dụ: để chuyển 0,5 thành phần trăm, 0,5 x 100 = 25%
• Trường hợp thứ hai liên quan đến một phân số. Nếu số đã cho ở dạng phân số, trước tiên hãy chuyển nó thành giá trị thập phân và nhân với 100. Ví dụ: để tìm tỷ lệ phần trăm của 1/6: 0,1666 x 100 = 16,7%.

ví dụ 1

Tính phần trăm của các giá trị sau:

1. 25 trên 200?

Lời giải
(25/200) × 100
Chia tử số cho mẫu số;
= (1/8) × 100
= (1 × 100) / 8
= 100/8
= 25/2
= 12 .5%

2. 95 trên 150?

Giải
(95/150) × 100 Rút gọn
phân số và nhân với 100
= (19/30) × 100
= (19 × 100) / 30
= 1900/30 rút gọn
phân số;
= 63 ¹ / ₃ %

3. 22 trên 44?

Lời giải
(22/44) × 100 Rút gọn
phân số;
= (1/2) × 100
= (1 × 100) / 2
= 100/2
= 50%

4. 30 trong số 150?

Lời giải
(30/150) × 100
Đơn giản hóa phân số;
= (1/5) × 100
= (1 × 100) / 5
= 100/5 = 20%

5. 250 trên 1200?

Lời giải
(250/1200) × 100
Hủy tử số và mẫu số;
= (5/24) × 100
= (5 × 100) / 24
= 500/24 ​​= 125/6
= 20 ⁵ / ₆ %

6. 86 trên 2580?

Giải pháp
(86/2580) × 100
đơn giản hóa phân số bằng cách hủy bỏ;
= (1/30) × 100
= (1 × 100) / 30
= 100/30 rút gọn
phân số;
10/3
= 3 ^1/ ₃ %

Ví dụ 2

Một lớp học có tổng số 120 học sinh. Tính tỉ lệ phần trăm số nữ nếu trong số họ có 60 em?

Giải pháp

Tổng số học sinh cả lớp = 120

Tổng số nữ = 60

Do đó, tỷ lệ trẻ em gái được tính là:

(60 × 100) / 120

= 600/12 = 50

Do đó, 50% học sinh là nữ.

Ví dụ 3

150 sinh viên có mặt trong khán phòng của trường. Nếu số học sinh nam và nữ có mặt trong hội trường lần lượt là 80 và 70. Tính tỉ lệ nam sinh có mặt trong khán phòng?

Giải pháp

Tổng số sinh viên có mặt trong khán phòng = 150

Số con trai = 80

Tỷ lệ trẻ em trai = (80 x 100) / 150

= 53,33%

Câu hỏi thực hành

1. Tính thành phần phần trăm của các số sau
2. 600 trên 2700?
3. 70 trên 150?
4. 1000 trên 1200?
5. 100 của 450
6. Trong số 500 điểm, James chỉ ghi được 350 điểm trong khi người bạn Peter của anh đạt 620 trên 800 điểm. Tìm phần trăm số hiệu của chúng?
7. Tổng diện tích của một mảnh đất là 6000 mét vuông. Nếu 4500 mét vuông được sử dụng để xây dựng, thì tỷ lệ phần trăm sẽ là bao nhiêu phần trăm còn lại nếu không xây dựng.
8. Một người bán hàng đã mua 600 quả chuối và 800 quả cam. Ông phát hiện ra rằng 8% chuối và 15% chuối bị thối. Tính thành phần phần trăm số quả còn lại?
9. Một người phụ nữ có mức lương hàng tháng là $Nếu chi tiêu hàng tháng cho thực phẩm là $250. Cô ấy tiết kiệm được bao nhiêu phần trăm tiền lương hàng tháng?
10. Sam đạt 43/50 điểm môn Toán, 62/75 môn Thống kê và 85/100 môn Vật lý. Môn học nào anh ấy đạt tỷ lệ cao nhất?

Xem thêm:

Phương pháp giải tỷ lệ nghịch nhanh gọn nhất

Tỷ lệ phần trăm chuyển đổi – Phương pháp giải hiệu quả nhất