Cách giải Vectơ Phủ định nhanh chóng chi tiết nhất

Nếu có vô hướng âm thì cũng có thể có vectơ âm ? Nó là! Trên thực tế, một vectơ âm là:

“Một vectơ có độ lớn bằng với độ lớn của vectơ tham chiếu, nhưng hướng của nó ngược với hướng của vectơ tham chiếu.”

Trong bài viết này, chúng ta sẽ thảo luận về các chủ đề sau liên quan đến vectơ âm:

• Phủ định của một vectơ là gì?
• Cách tìm một vectơ phủ định

Phủ định của một vectơ là gì?

Các vectơ có cùng độ dài với một vectơ cụ thể nhưng ngược hướng được gọi là vectơ âm. Một dấu âm sẽ đảo ngược hướng của một vectơ và làm cho nó trở thành một vectơ âm. Vectơ chỉ âm đối với vectơ khác.

Ví dụ , nếu một vectơ PQ hướng từ trái sang phải, thì vectơ QP sẽ hướng từ phải sang trái. Vì các hướng này ngược nhau nên ta nói rằng PQ = – QP. Nghĩa là, QP là vectơ âm của PQ, như được mô tả trong hình dưới đây. Điều quan trọng cần lưu ý là vectơ PQ và vectơ QP có cùng độ lớn nhưng ngược hướng, làm cho chúng trở thành vectơ âm của nhau

Độ lớn hoặc độ dài của vectơ không được âm; nó có thể là 0 hoặc dương. Dấu âm được sử dụng ở đây để chỉ ra rằng vectơ có hướng ngược lại với vectơ tham chiếu.

Về mặt toán học, chúng ta có thể nói rằng hai vectơ A và B là âm của nhau nếu chúng thỏa mãn hai điều kiện sau:

A = – B (“Vectơ B là âm của vectơ A” )

Nếu

| A | = | B |    (Độ lớn bằng nhau) và

A ↑ và B ↓   hoặc   A ↓ và B ↑    (Hướng ngược nhau).

Một phương pháp đơn giản khác để tìm xem hai vectơ có phải là âm của nhau hay không là so sánh tọa độ của chúng. Nếu tọa độ của các vectơ có giá trị bằng nhau nhưng ngược dấu thì các vectơ sẽ là âm của nhau. Ví dụ, hãy xem xét các vectơ A = (ax1, ay1) và B = (bx1, by1). Chúng ta nói rằng vectơ B là âm của vectơ A , hoặc:

A = – B

Nếu

ax1 = -bx1 và ay1 = -by1.

Tiêu chí này đủ cho thấy B là vectơ âm của A và ngược lại.

 Làm thế nào để tìm một vectơ phủ định?

Ý tưởng cơ bản đằng sau việc tìm vectơ âm của một vectơ đã cho là tìm hai thành phần của vectơ đã cho (tức là độ lớn của vectơ và hướng) và sau đó tìm một vectơ có cùng độ dài hướng ngược lại. Hai vectơ như vậy sẽ là vectơ âm của nhau.

Việc tìm vectơ âm của một vectơ đã cho có thể được thực hiện bằng cách đặt một dấu âm trước nó. Ví dụ, cho X là một vectơ. Để có được vector âm X , chúng ta nhân X bằng -1, làm cho nó – X. Hãy nhớ rằng độ lớn của vector – X là giống như của vector X .

Các ví dụ

Phần này trước tiên sẽ xem xét các ví dụ khác nhau trong đó chúng ta tìm vectơ âm bằng cách so sánh các thành phần của vectơ tham chiếu. Sau đó, chúng ta sẽ thảo luận thêm một số ví dụ và các giải pháp từng bước của chúng để phát triển sự hiểu biết sâu sắc hơn về vectơ âm.

ví dụ 1

Cho vectơ P = (2, 4), xác định âm của P.

Giải pháp

Theo định nghĩa, âm của một vectơ có cùng độ lớn với hướng ngược lại của vectơ tham chiếu. Trong trường hợp này, vectơ tham chiếu là P và hướng của nó là 2 điểm ở bên phải dọc theo trục x và 4 điểm hướng lên dọc theo trục y. Do đó, để tìm vectơ âm của P , chúng ta giữ nguyên độ lớn và nhân vectơ tham chiếu P với -1. Điều này mang lại cho chúng tôi:

– P = (-2, -4)

Hoặc là

– P = – (2, 4)

Bây giờ, hướng của vectơ âm có thể được hiểu là 2 điểm ở bên trái dọc theo trục x và 4 điểm hướng xuống dọc theo trục y. Điều này rõ ràng là ngược với hướng của vectơ tham chiếu P.

Ví dụ 2

Cho hình bình hành ABCD trong hình bên, xác định các vectơ nào bằng nhau và âm của nhau.

Giải pháp

Theo định nghĩa, hai vectơ chỉ có thể bằng nhau nếu chúng có cùng độ lớn và cùng hướng. Trong hình bình hành ABCD, vectơ AB song song với vectơ CD, ngược lại vectơ BC song song với vectơ DA. Ngoài ra, vectơ AB và vectơ CD cùng phương. Do đó, chúng ta có thể nói rằng chúng là các vectơ bằng nhau, tức là:

AB = CD (Các vectơ bằng nhau)

Tương tự, vectơ BC và vectơ DA có cùng độ dài nhưng ngược hướng. Do đó chúng là âm của nhau, tức là:

BC = – DA (Vectơ âm)

Xem thêm:

Vectơ bằng nhau là như thế nào? Những nội dung cơ bản

Kiến thức mới nhất về Vectơ kết quả

Ví dụ 3

Hãy xem xét hình ảnh được đưa ra dưới đây. So sánh hai vectơ P và Q và xác định xem chúng có phải là âm của nhau hay không.

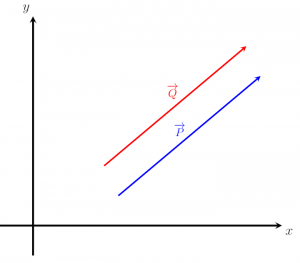
Giải pháp

Ví dụ này rất đơn giản. Từ hình trên có thể thấy vectơ P và vectơ Q có cùng độ lớn. Hai vectơ cũng chỉ cùng phương. Do đó, so sánh nhanh hai vectơ cho thấy chúng bằng nhau, nhưng chúng không phải là âm của nhau.

P = Q

Ví dụ 4

Xác định âm của vectơ OW, điểm ban đầu của nó là O = (2, 5) và điểm cuối cùng của nó là W = (5, 2).

Giải pháp

Để xác định âm của vectơ OW đã cho, ta nhân tọa độ của nó với -1 để được – OW. Như vậy, điểm đầu và điểm cuối của vectơ âm là:

-O = (-2, -5) và -W = (-5, -2)

Tiếp theo, chúng tôi xác định độ lớn của cả hai vectơ để kiểm tra xem chúng vẫn giống nhau.

Độ lớn được tính như sau:

| OW | = √ (5 – 2) ^ 2 + (2 – 5) ^ 2

| OW | = √ 3 ^ 2 + (-3) ^ 2

| OW | = √ 18

Do đó, độ lớn của vectơ OW được tìm thấy là xấp xỉ 4,242 đơn vị.

Tương tự, độ lớn của vectơ – OW là:

| – OW | = √ (-5 + 2) ^ 2 + (- 2 + 5) ^ 2

| – OW | = √ (-3) ^ 2 + (3) ^ 2

| – OW | = √ 18

Do đó, độ lớn của vectơ – OW cũng được tìm thấy là xấp xỉ 4,242 đơn vị. Do đó, hai vectơ có cùng độ dài nhưng ngược hướng, nghĩa là vectơ – OW là vectơ âm của OW.

OW = – OW

Ví dụ 5

Xác định vectơ nào sau đây bằng nhau và là âm của nhau: a = (1; 3), b = (-1; -3) và c = (1; 3).

Giải pháp

Chúng ta sẽ so sánh độ lớn và hướng của các vectơ đã cho để xác định vectơ nào bằng nhau và âm của nhau.

Đầu tiên, chúng tôi xác định độ lớn của các vectơ đã cho:

Cho vectơ a = (1; 3)

| a | = √1 ^ 2 + 3 ^ 2

| a | = √10

Cho vectơ b = (-1; -3)

| b | = √-1 ^ 2 + (-3) ^ 2

| b | = √1 + 9

| b | = √10

Cho vectơ c = (1; 3)

| c | = √1 ^ 2 + 3 ^ 2

| c | = √10

Rõ ràng là | a | = | b | a | = | c |, và | b | = | c | Do đó, độ lớn của vectơ a, vectơ b và vectơ c là như nhau.

Để so sánh hướng, chúng ta có thể vẽ ba vectơ trên mặt phẳng tọa độ, như trong hình dưới đây. Có thể nhận thấy rằng các vectơ a và c có cùng độ lớn và chúng cũng hướng cùng phương. Mặt khác, vectơ b hướng ngược lại. Do đó, chúng ta có thể kết luận như sau:

Các vectơ a và c là các vectơ bằng nhau,

a = c

và cặp vectơ a , b và cặp vectơ b , c là vectơ âm.

a = – b

c = – b

Ví dụ 6

Xác định giá trị của x để hai vectơ A = (4, 10) và B = (2x, 5x) là âm của nhau.

Giải pháp

Chúng ta biết rằng hai vectơ là âm của nhau nếu độ lớn của chúng bằng nhau và hướng của chúng ngược nhau. Chúng tôi sử dụng điều này để xác định giá trị của x chưa biết như sau:

A = – B => (2, 10) = – (2x, 5x)

Bằng cách đặt các thành phần tương ứng bằng nhau, chúng ta nhận được:

2 = -2x

Và

10 = -5x

Bằng cách đơn giản hóa phương trình trên, chúng ta nhận được:

x = -2

Như vậy, khi x = -2 thì hai vectơ A và B là âm của nhau.

Ví dụ 7

Xác định giá trị của n để hai vectơ A = (-5, -1, 3n) và B = (-5, -1, -9) là âm của nhau.

Giải pháp

Chúng ta biết rằng hai vectơ bằng nhau nếu độ lớn của chúng bằng nhau và hướng của chúng ngược nhau. Chúng tôi sử dụng điều này để xác định giá trị của n chưa biết như sau:

A = – B  => (-5, -1, -3n) = – (-5, -1, -9)

Bằng cách đặt các thành phần tương ứng bằng nhau, chúng ta nhận được:

-5 = 5, -1 = 1 và 3n = 9

-3n = -9

Bằng cách đơn giản hóa phương trình trên, chúng ta nhận được:

n = 3

Như vậy, khi n = 3 thì hai vectơ A và B là âm của nhau.

Câu hỏi thực hành

Tìm âm của các vectơ sau:

1. A = (-1, -2/3, 0)
2. T = (0, 2, -1)
3. V = (2, 5) và D = (3, -2). Ngoài ra, hãy kiểm tra xem hai vectơ có phải là âm của nhau hay không.
4. F = (4, 10), G = (5, 5) và H = (-4, -10). Đồng thời kiểm tra xem các vectơ đã cho có phải là âm của nhau hay không.
5. Xác định giá trị của n để hai vectơ A = (-2n, -3, -2) và B = (8, 3, 2) là âm của nhau.
6. Vectơ OA với điểm đầu O = (-1, 0, 3) và điểm cuối A = (5, 2,0)
7. Vectơ UV, trong đó U = (1, -2, 0) và V = (-2, 2, 0).

Câu trả lời

1. Âm của vectơ A sẽ là – A = (1, 2/3, 0).
2. Âm của vectơ T sẽ là – T = (0, -2, 1).
3. Âm của vectơ V sẽ là – V = (-2, -5), âm của vectơ D sẽ là – D = (-3, 2). Rõ ràng, hai vectơ không phải là âm của nhau.
4. Âm của vectơ F sẽ là – F = (-4, -10). Âm của vectơ G sẽ là – G = (-5, -5), và âm của vectơ H  sẽ là – H = (4,10). Rõ ràng, hai vectơ F và G không phải là âm của nhau mà vectơ F và H là F = – H.
5. Bằng cách so sánh các thành phần của hai vectơ, chúng ta thấy rằng, khi n = 4, hai vectơ A và B sẽ là âm của nhau.
6. Độ lớn của véctơ OA  là | OA | = 7 đơn vị, và âm của vectơ OA sẽ là – OA. Độ lớn của nó phải bằng độ lớn của vectơ OA . Do đó, vectơ – OA sẽ bắt đầu tại điểm -O = (1, 0, -3) và kết thúc tại điểm -A = (-5, -2, 0).
7. Độ lớn của vectơ UV là | UV | = 5 đơn vị, và âm của vectơ UV sẽ là – UV. Độ lớn của nó phải giống như độ lớn của vectơ UV. Do đó, vectơ – UV sẽ bắt đầu tại điểm -U = (-1, 2, 0) và kết thúc tại điểm -V = (2, -2, 0).