Hình học Vectơ – Giải thích & Ví dụ dễ hiểu nhất

Mô hình hóa là quan trọng trong tất cả các nhánh của toán học, bao gồm cả hình học vectơ . Đây là:

“Nghiên cứu về biểu diễn hình học của vectơ, cụ thể là biểu diễn dưới dạng
các đoạn thẳng hoặc mũi tên có hướng.”

Trong chủ đề này, chúng ta sẽ thảo luận về các khía cạnh sau của hình học vectơ:

• Vectơ trong Hình học là gì?
• Định nghĩa vectơ trong hình học

Vectơ trong Hình học là gì?

Các đại lượng có cả độ lớn và hướng được gọi là vectơ. Chúng ta có thể sử dụng một đồ thị để biểu diễn các vector một cách trực quan. Ví dụ, một vectơ nối hai điểm A và B được gọi là:

AB

Một vectơ ở vị trí chuẩn sẽ có gốc là điểm bắt đầu của nó.

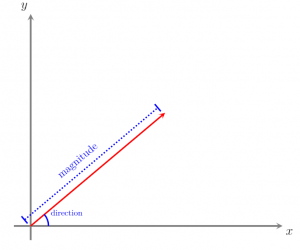
Ở dạng thành phần hoặc dạng cột, vectơ được viết trong một cặp có thứ tự (x, y). Một vectơ được viết dưới dạng này bắt đầu tại điểm gốc và kết thúc tại điểm của cặp có thứ tự.

Các tiêu cực của một trao vector được tìm thấy bằng cách đảo ngược hướng của vector. Trong trường hợp này, độ lớn (hoặc độ dài) của nó giống như độ lớn của vectơ ban đầu.

Ví dụ: vectơ:

BA = – AB

là âm của vectơ AB, và:

|| BA || = || – AB || = || AB ||

Định nghĩa vectơ trong hình học

Cho hai điểm P và Q, mũi tên từ P đến Q sẽ có độ dài và hướng.

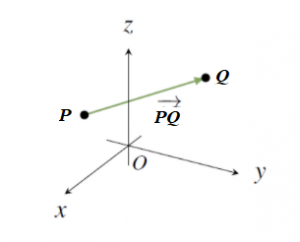
Giả sử P và Q là hai điểm tùy ý trong không gian R ³ . Đoạn thẳng từ P đến Q được kí hiệu là PQ. Trong hình học, đây được gọi là vectơ từ P đến Q.

Vectơ này sẽ có độ lớn và hướng. Điểm P được gọi là đuôi (hoặc điểm đầu) của vectơ PQ, còn điểm Q được gọi là đỉnh (hoặc đầu hoặc điểm cuối) của vectơ PQ . Chiều dài của nó được ký hiệu là || PQ ||.

Giả sử điểm P có tọa độ (x ₁ , y ₁ ) và điểm Q có tọa độ (x ₂ , y ₂ ) trong mặt phẳng R ² . Khi đó độ dài của vectơ PQ được xác định theo các bước dưới đây.

Bước 1: Đầu tiên, trừ thành phần đầu tiên của điểm P với thành phần đầu tiên của điểm Q. Sau đó, tìm bình phương của hiệu số kết quả.

Bước 2: Tương tự, lấy thành phần thứ hai của điểm P trừ đi thành phần thứ hai của điểm Q và bình phương số đó.

Bước 3: Sau đó, bạn hãy cộng hai hình vuông lại với nhau.

Bước 4: Cuối cùng, lấy căn bậc hai của số bạn tìm thấy ở bước ba. Số vô hướng này sẽ là độ dài của vectơ.

• Lưu ý rằng độ dài hoặc độ lớn của một vectơ là một đại lượng vô hướng.

Các ví dụ

Bây giờ, chúng ta hãy thử một vài ví dụ để thực hành làm việc với hình học vectơ.

ví dụ 1

Cho hai điểm O tại gốc tọa độ (0,0) và A có tọa độ (3,2), xác định độ dài || OA ||.

Giải pháp:

So sánh các thành phần, chúng tôi nhận được

(x ₁ , y ₁ ) = (0,0) và (x ₂ , y ₂ ) = (3, 2).

Sử dụng công thức ở trên để tìm độ dài của hai vectơ a, ta có:

‖ OA ‖ = √ ((x_2-x_1) ^ 2 + (y_2 – y_1) ^ 2).

Bây giờ, thay thế các giá trị trên cho chúng ta:

= √ ((0-3) ^ 2 + (0-2) ^ 2).

Đơn giản hóa, chúng tôi nhận được:

‖ OA ‖ = √ ((- 3) ^ 2 + (- 2) ^ 2)

Đơn giản hóa bổ sung mang lại cho chúng tôi:

‖ OA ‖ = √ (9 + 4)

‖ OA ‖ = √13.

Như vậy, || OA || = √13 là độ dài của vectơ nối hai điểm.

Lưu ý rằng nếu điểm ban đầu hoặc điểm cuối của một vectơ ở gốc tọa độ, tức là, nếu vectơ được viết ở dạng chuẩn, thì độ lớn của OA là:

|| A || = √ (x ² + y ² )

Trong đó A = OA = (x, y).

Ví dụ 2

Cho hai điểm A = (3, 2) và B = (2, 2), hãy xác định độ dài vectơ AB.

Giải pháp :

So sánh các thành phần, chúng tôi nhận được

(x ₁ , y ₁ ) = (3, 2) và (x ₂ , y ₂ ) = (2, 2).

Sử dụng công thức nêu trên để tìm độ dài của hai vectơ a, chúng ta có

‖ AB ‖ = √ ((x_2-x_1) ^ 2 + (y_2 – y_1) ^ 2)

 Bây giờ, thay thế các giá trị trên cho chúng ta:

‖ AB ‖ = √ ((3-2) ^ 2 + (2-2) ^ 2)

Đơn giản hóa, chúng tôi nhận được:

‖ AB ‖ = √ ((1) ^ 2 + (0) ^ 2)

‖ AB ‖ = √1 + 0

‖ AB ‖ = 1

Như vậy, || AB || = 1 là độ dài của vectơ nối hai điểm.

Ví dụ 3

Trong hình dưới đây, cho trước hai vectơ AB = 2 a và BC = 3 b . Điểm D là trung điểm của BE và E là trung điểm của BC.

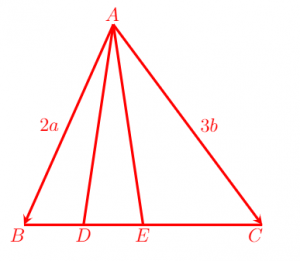
Sử dụng thông tin đã cho ở trên, hãy xác định các vectơ sau theo a và b:

• (a) BC
• (b) BD
• (c) QUẢNG CÁO

Giải pháp:

• (a) Sử dụng định luật tam giác của phép cộng vectơ, ta có

BC = BA + AC

Chúng ta lưu ý mối quan hệ giữa BA và vectơ có độ dài đã biết, AB :

= (- AB ) + AC

Thay các giá trị đã biết của AB và AC ta được :

= -2 a + 3 b .

Như vậy, BC = -2 a + 3 b là độ dài của vectơ.

• (b) Vì E là trung điểm của BC và D là trung điểm của BE nên D là 1/4 khoảng cách BC:

BD = ¼ BC

Thay giá trị của BC tìm được trong phần (a) cho ta:

= ¼ (-2 a + 3 b )

= -1/2 a + 3/4 b .

Như vậy, BD = -1/2 a + 3/4 b là độ dài của vectơ.

• (c) Sử dụng định luật tam giác của phép cộng vectơ, ta có:

AD = AB + BD

Thay các giá trị đã biết của AB và AC ta được:

= 2 a + (-1/2 a + 3/4 b )

Điều này có thể được đơn giản hóa:

= (2 a + -1/2 a ) + 3/4 b

= 3/2 a + 3/4 b .

Như vậy, AD = 3/2 a + 3/4 b là độ dài của vectơ.

Ví dụ 4

Gọi A = (2, 0, -4) và B = (2, 1, -2) là hai điểm trong không gian R ³ . Nếu 2 a – || b || b = 3/2 ( a – 2 x ), trong đó a = OA , b = OB và x = OX và X = (x ₁ , x ₂ , x ₃ ), tìm giá trị của x ₁ , x ₂ và x ₃ .

Giải pháp :

Chúng tôi có mối quan hệ:

2 a – || b || b = 3/2 ( a – 2 x ),

Trong đó a = (2, 0, -4), b = (2, 1, -2) và x = (x ₁ , x ₂ , x ₃ ).

Trước hết chúng ta sẽ đánh giá tiêu chuẩn (độ lớn) || b || bằng cách sử dụng các định nghĩa trước đó và quy trình để tìm độ lớn của một vectơ có điểm bắt đầu tại điểm gốc. Điều này mang lại cho chúng tôi:

|| b || = √ (2 ² + 1 ² + (-2) ² )

= √ (4 + 1 + 4)

= √9

= 3

Do đó, || b || = 3. Bây giờ chúng ta có:

|| b || b = 3 (2, 1, -2)

= (3 ∙ 2, 3 ∙ 1, 3 ∙ (-2))

= (6, 3, -6)

Tương tự, chúng ta có:

2 a = 2 (2, 0, -4) = (4, 0, -8).

Do đó, phía bên tay trái sẽ trở thành

2 a – || b || b = (4, 0, -8) – (6, 3, -6)

= (4-6, 0-3, -8 – (- 6))

= (-2, -3, -8 + 6)

= (-2, -3, -2).

Phía bên tay phải sẽ trở thành:

3/2 ( a – 2 x ) = 3/2 ((4, 0, -8) – 2 (x ₁ , x ₂ , x ₃ ))

= 3/2 ((4, 0, -8) – (2x ₁ , 2x ₂ , 2x ₃ ))

= 3/2 (4-2x ₁ , 2x ₂ , -8-2x ₃ ).

Bây giờ thay các giá trị này vào các vế trái và phải của phương trình, chúng ta nhận được:

2 a – || b || b = 3/2 ( a – 2 x )

(-2, -3, -2) = 3/2 (4-2x ₁ , 2x ₂ , -8-2x ₃ )

2 (-2, -3, -2) = 3 (4-2x ₁ , 2x ₂ , -8-2x ₃ )

(-4, -6, -4) = (3 (4-2x ₁ ), 3 (2x ₂ ), 3 (-8-2x ₃ )).

So sánh các thành phần x, y và z cho chúng ta:

-4 = 3 (4-2x ₁ )

-4 = 12 – 6x ₁

6x ₁ = 12 – 4

6x ₁ = 8

x ₁ = 8/6

Do đó, x ₁ = 4/3.

-6 = 3 (2x ₂ )

-6 = 6x ₂

x ₂ = -6/6

Do đó, x ₂ = -1

-4 = 3 (-8-2x ₃ )

-4 = -24 -6x ₃

6x ₃ = -24 + 4

6x ₃ = -20

x ₃ = -20/6

Do đó, x ₃ = -10/3.

Như vậy:

x ₁ = 4/3, x ₂ = -1 và x ₃ = -10/3.

Câu hỏi thực hành

1. Cho hai điểm V = (2, 5, 1) và C = (3, -2, 1), xác định độ dài của vectơ VC .
2. Cho hai điểm G = (5, 5) và H = (4, -10), xác định || OG || và || OH || ² , trong đó O = (0, 0) là gốc tọa độ.
3. Trong tam giác ABC, CB = 4CX, XA = 5XY và Z là trung điểm của AB. Cho CX = m và BZ = n .

• (a)Xác định độ dài của XB và XA theo m và n
• (b) Chứngtỏ rằng CZ = (4 m + n )
• (c)Đánh giá ‖ CY ‖ / ‖ CZ ‖ và (khu vực ACY) / (khu vực ACZ)

1. Cho ABCDEF là một lục giác đều và AB = n .

• (a)Giải thích tại sao vectơ ED = n .
• (b)Nếu BC = m và CD = p, tìm AC và AD
• (c)Tìm FD .

1. Cho đoạn thẳng ABC, BC = 3 AB . Nếu OA = a và AB = b, biểu thị OC theo a và b .

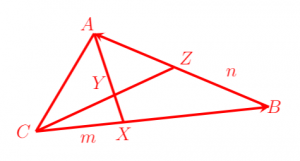
 Câu trả lời

1. || VC || = 5√2
2. || OG || = 5√2, || OH || ² = 116
3. Trong tam giác đã cho,

• (a) XB= 3 m và XA = 3 m + 2 n
• (b) CZ = CB + BZ = 4m + n
• (c)Các giá trị là: ‖ CY ‖ / ‖ CZ ‖ = 2/5, và (diện tích ACY) / (diện tích ACZ) = 2/5

4. Cho lục giác đều ABCDEF và AB= n.

• (a)Nó đối diện với AB .
• (b)Nếu BC = m và CD = p . Khi đó AC = n + m và AD = n + m + p
• (c) FD= – ( m + n ) (tức là âm của vectơ AC ).

1. OC = a +4 b

Xem thêm:

Chi tiết cách tìm một đơn vị Vector chỉ trong giây lát

Góc giữa hai Vectơ – Giải thích và Ví dụ