Xâm lược là gì? xem xong 5 phút hiểu luôn.

Định nghĩa

Một đường cong có được bằng cách gắn một sợi dây là tưởng tượng, sau đó cuộn và tháo nó ra trên đường cong đã cho được gọi là bất khả quy trong hình học vi phân. Involute hoặc evolvent là quỹ tích của phần cuối tự do của chuỗi này

Sự phát triển của một bất biến của một đường cong được quy về đường cong ban đầu đó. Nói cách khác, quỹ tích của tâm cong của một đường cong được gọi là tiến hóa và bản thân đường cong có dấu vết được gọi là bất khả quy của nó.

Đây là một phần của một nhánh hình học đặc biệt được gọi là Hình học vi phân của đường cong. Nó nói về các đường cong trơn nằm trong không gian Euclide và việc áp dụng các phương pháp tính tích phân và vi phân khác nhau trên chúng. Các hình dạng liên quan đến một số đường cong khác được gọi là bất biến. Điều này được Christine Huygens phát hiện năm 1673. Ông là một nhà toán học và vật lý học người Hà Lan.

Sự xâm phạm của các đường cong

Chúng ta hãy cùng tìm hiểu về các bất khả quy của các đường cong khác nhau như hình dưới đây:

• Sự xâm phạm của một vòng kết nối
• Sự xâm phạm của một dây xích
• Sự xâm phạm của một Deltoid
• Sự xâm phạm của một Parabol
• Sự xâm phạm của một hình elip

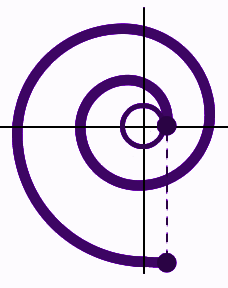
1) Sự xâm phạm của một vòng tròn: Nó tương tự như hình xoắn ốc Archimedes.

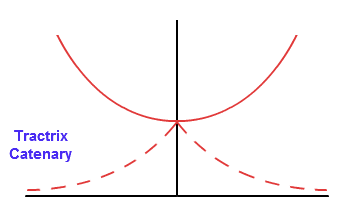
2) Sự xâm phạm của một dây xích – Nó là một đường cong tương tự như cáp treo được hỗ trợ bởi các đầu của nó. Vì vậy, nó là một chuỗi treo hình chữ U trông giống như một parabol. Đường ma trận là bất khả quy của dây xích qua đỉnh.

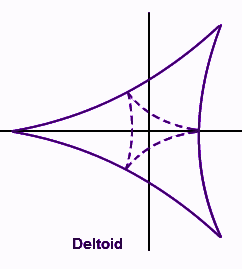
3) Sự xâm lấn của một Deltoid- Nó là một đường cong ba lá với ba điểm chóp. Nó giống với đồng bằng chữ cái Hy Lạp.

4) Sự xâm phạm của một Parabol –

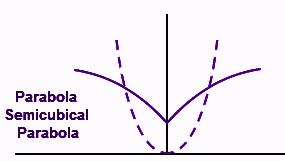
5) Sự xâm phạm của một hình elip –

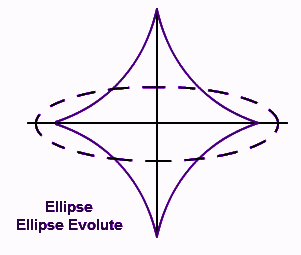
Phương trình

• Vòng kết nối xâm phạm
• Catenary Involute
• Deltoid Involute

Circle Involute: x = r (cos t + t sin t), y = r (sin t – t cos t), trong đó, r = bán kính của đường tròn, t = tham số góc tính bằng radian.

Catenary Involute: x = t – tanh t, y = sech t, trong đó t là tham số.

Deltoid Involute: x = 2 r cos t + r cos 2t, y = 2 r sin t – r sin 2t

trong đó, r = bán kính của vòng tròn lăn liên quan đến sự hình thành deltaid.

Sự xâm phạm của một vòng kết nối

Sự xâm phạm của một vòng tròn là một khái niệm thực tế và cũng có nhiều ứng dụng thực tế khác nhau. Nó chủ yếu được sử dụng để thiết kế bánh răng hoặc bánh răng được sử dụng trong các máy quay. Nó trông giống như một hình xoắn ốc Archimedes. Các phương trình tham số của nó được hiển thị bên dưới:

• • Trong tọa độ Descartes:

Nếu r là bán kính của đường tròn và tham số góc là t thì

x = r (cos t + t sin t)

y = r (sin t – t cos t)

• • Trong Tọa độ Cực:

Nếu r và θ là các tham số thì r = a sec α

θ = tan α – α, trong đó, a là bán kính của đường tròn.

• • Chiều dài vòng cung của vòng tròn không tính:

Độ dài của cung bất biến của đường tròn là

L = (r / 2) t ²

Làm thế nào để vẽ Involute

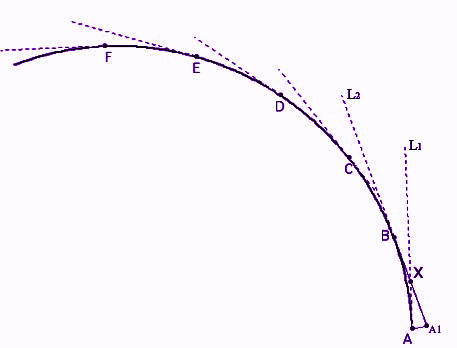
Chúng ta hãy học cách vẽ không xâm phạm theo các bước sau:

1. Vẽ một số tiếp tuyến với các điểm đã cho trên đường cong
2. Chọn 2 đường tiếp tuyến lân cận.
   1. Mở rộng chúng theo các hướng ngược lại
   2. Tìm giao điểm của chúng.
   3. Bây giờ, hãy lấy điểm cuối đó làm trung tâm
   4. Lấy khoảng cách giữa tâm đã cho và điểm của tiếp tuyến 1t.
   5. Một vòng cung sẽ được vẽ.

Như hình sau, cho L ₁ và L2 là hai tiếp tuyến liên tiếp

Các giao điểm này là X và XA là bán kính.

Vậy thu được cung AA ₁ .

3. Ta lấy thêm 2 tiếp tuyến lân cận L ₂ và L ₃ .
   1. Lấy giao điểm Y của chúng làm tâm
   2. Lấy khoảng cách YA1 làm bán kính
   3. Vẽ cung tròn A ₁ A ₂

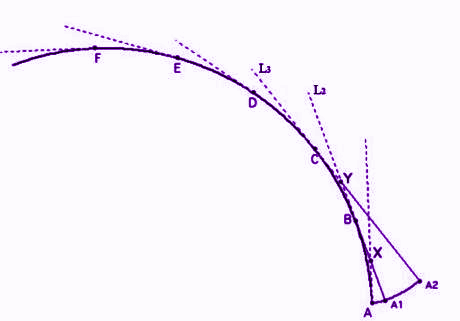
4. Lặp lại quá trình tương tự cho phần còn lại của các tiếp tuyến. Bằng cách này, chúng ta sẽ có được một đường cong từ các vòng cung được xây dựng từ bây giờ. Và chúng ta sẽ nhận được yêu cầu bất khả xâm phạm của đường cong.

Ứng dụng

Các bất biến của đường cong có nhiều ứng dụng trong các ngành công nghiệp và doanh nghiệp.

• Các ngành công nghiệp bánh răng – Để chế tạo răng cho hai máy quay và bánh răng.
• Nén cuộn và Nén khí – Chúng được làm theo hình dạng này để giảm tiếng ồn và làm cho chúng hoạt động hiệu quả.

• Những từ tiếng anh hay và ý nghĩa nhất
• Giới từ at, on, in được dùng như thế ? Cùng tìm hiểu.
• Bảng tính số hợp lý là gì? Xem xong 5 phút hiểu luôn.