Trong đó α biểu thị diện tích của tam giác và (x1,y1) , (x2,y2) a n d(x3,y3) , đại diện cho các đỉnh của tam giác.


Công thức tìm diện tích có thể được biểu diễn dưới dạng các định thức như dưới đây.
α =12∣∣∣∣x1x2x3y1y2y3111∣∣∣∣
Như chúng ta biết giá trị của một định thức có thể là giá trị âm hoặc giá trị dương nhưng vì chúng ta đang nói về diện tích và nó không bao giờ có thể được coi là giá trị âm, do đó chúng ta lấy giá trị tuyệt đối của định thức để thu được.
Nếu diện tích của tam giác đã cho thì chúng ta sử dụng cả giá trị âm và dương của định thức.
Ngoài ra, nếu ba điểm thẳng hàng, chúng ta sẽ được để lại bằng một đường thẳng thay vì một hình tam giác và vì diện tích bao quanh bởi một đường thẳng bằng không, do đó giá trị của định thức cũng sẽ bằng không.
Lưu ý những điểm đã đề cập ở trên, chúng ta hãy cố gắng mở rộng yếu tố xác định biểu thị khu vực bằng cách sử dụng các kỹ thuật mở rộng định thức bằng cách sử dụng phần tử và đồng yếu tố .
Do đó, α =12[x1(y2–y3) +x2(y3–y1) +x3(y1–y2) ]
Do đó, chúng ta thấy rằng cách các định thức được áp dụng để thực hiện các phép tính dễ dàng. Bây giờ chúng ta hãy thử áp dụng các định thức này để tìm ra diện tích của hình tam giác.
Ví dụ để tìm Diện tích tam giác bằng cách sử dụng Định thức
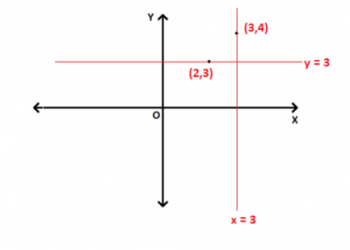
Ví dụ: Tìm diện tích tam giác có các đỉnh là A (0,0), B (3,1) và C (2,4).
Giải pháp: Sử dụng các định thức, chúng ta có thể dễ dàng tìm ra diện tích của tam giác có được bằng cách nối các điểm này bằng công thức
α =12∣∣∣∣x1x2x3y1y2y3111∣∣∣∣.
Thay thế các giá trị tương ứng trong yếu tố quyết định chúng ta có
α =12∣∣∣∣032014111∣∣∣∣
Mở rộng định thức ở trên bằng cách sử dụng các kỹ thuật mở rộng định thức mà chúng ta nhận được,
α =12[ 0 ( 1 – 4 ) – 0 ( 3 – 2 ) + 1 ( 12 – 2 ) ]
⇒ α = 5 u n i t s <