Tam giác 30-60-90 là gì? Hướng dẫn cách giải hay nhất
3 Tháng Ba, 2021Bây giờ khi chúng ta đã hoàn thành với tam giác vuông và các tam giác vuông đặc biệt...
Contents
Định lý Pitago còn được gọi là ‘ định lý Pythagoras ‘ được cho là công thức nổi tiếng nhất trong toán học xác định mối quan hệ giữa các cạnh của một tam giác vuông.
Định lý được cho là của một nhà toán học và triết học người Hy Lạp tên là Pythagoras (569-500 TCN) . Ông có nhiều đóng góp cho lĩnh vực toán học, nhưng Định lý Pitago là quan trọng nhất trong số đó.
Pythagoras được ghi nhận với một số đóng góp trong lĩnh vực toán học, thiên văn học, âm nhạc, tôn giáo, triết học … Một trong những đóng góp đáng chú ý của ông cho toán học là việc phát hiện ra Định lý Pythagore. Pythagoras đã nghiên cứu các cạnh của một tam giác vuông và phát hiện ra rằng, tổng bình phương của hai cạnh ngắn hơn của tam giác bằng bình phương của cạnh dài nhất.
Trong bài viết này, chúng ta sẽ tìm hiểu Định lý Pitago đòi hỏi gì , nghịch đảo của nó và công thức của Định lý Pitago . Trước khi đi sâu hơn vào chủ đề, chúng ta hãy nhớ lại về một tam giác vuông. Tam giác vuông là tam giác có một góc trong bằng 90 độ. Trong một tam giác vuông, hai chân ngắn gặp nhau một góc 90 độ. Cạnh huyền của tam giác là cạnh đối diện với góc 90 độ.
Định lý Pythagoras là một định luật toán học phát biểu rằng, tổng bình phương độ dài hai cạnh ngắn của tam giác vuông bằng bình phương độ dài cạnh huyền .
Định lý Pythagoras được viết theo phương pháp đại số là:
a 2 + b 2 = c 2
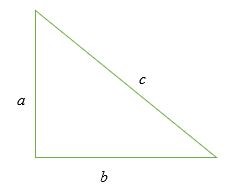

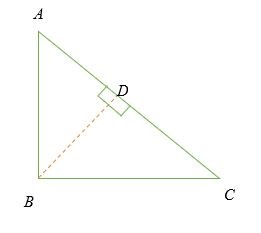

Xét một tam giác vuông ở trên.
Cho rằng:
∠ ABC = 90 °.
Gọi BD là đường vuông góc với cạnh AC.
∆s tương tự:
∆ADB và ∆ABC là các tam giác đồng dạng.
Từ quy tắc tương tự,
⇒ AD / AB = AB / AC
⇒ AD × AC = (AB) 2 —————– (i)
Tương tự như vậy;
∆BDC và ∆ABC là các tam giác đồng dạng. Vì thế;
⇒ DC / BC = BC / AC
⇒ DC × AC = (BC) 2 —————– (ii)
Bằng cách kết hợp phương trình (i) và (ii), chúng ta nhận được,
AD × AC + DC × AC = (AB) 2 + (BC) 2
⇒ (AD + DC) × AC = (AB) 2 + (BC) 2
⇒ (AC) 2 = (AB) 2 + (BC) 2
Do đó, nếu ta cho AC = c; AB = b và BC = b, khi đó;
⇒ c 2 = a 2 + b 2
Xem thêm:
Định lý chân Hypotenuse – Giải thích & Ví dụ đơn giản nhất
Định lý Góc ngoài đơn giản dễ hiểu nhất 2021
Có rất nhiều cách chứng minh Định lý Pitago được đưa ra bởi các nhà toán học khác nhau.
Một minh chứng phổ biến khác là vẽ 3 hình vuông sao cho chúng tạo thành một tam giác vuông ở giữa và diện tích của hình vuông lớn hơn (hình vuông ở cạnh huyền) bằng tổng diện tích của hai hình vuông nhỏ hơn ( những cái ở hai bên).
Hãy xem xét 3 hình vuông dưới đây:
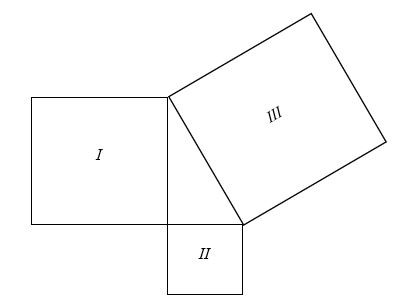

Chúng được vẽ theo cách mà chúng tạo thành một tam giác vuông. Bây giờ các vùng của chúng có thể được viết dưới dạng phương trình:
Diện tích hình vuông III = Diện tích hình vuông I + Diện tích hình vuông II
Giả sử độ dài của hình vuông I , hình vuông II và hình vuông III lần lượt là a, b và c.
Sau đó,
Diện tích hình vuông I = a 2
Diện tích hình vuông II = b 2
Diện tích hình vuông III = c 2
Do đó, chúng ta có thể viết nó là:
a 2 + b 2 = c 2
đó là một Định lý Pitago.
Các converse của Pythagore lý là một quy tắc được sử dụng để hình tam giác classify là một trong hai tam giác vuông, tam giác cấp tính hoặc tam giác tù.
Cho Định lý Pitago, a 2 + b 2 = c 2 thì;
ví dụ 1
Phân loại một tam giác có các kích thước là; a = 5 m, b = 7 m và c = 9 m.
Giải pháp
Theo Định lý Pitago, a 2 + b 2 = c 2 thì;
a 2 + b 2 = 5 2 + 7 2 = 25 + 49 = 74
Nhưng, c 2 = 9 2 = 81
So sánh: 81> 74
Do đó, c 2 > a 2 + b 2 (tam giác tù).
Ví dụ 2
Phân loại một tam giác có độ dài các cạnh a, b, c lần lượt là 8 mm, 15 mm và 17 mm.
Giải
a 2 + b 2 = 8 2 + 15 2 = 64 + 225 = 289
Nhưng, c 2 = 17 2 = 289
So sánh: 289 = 289
Do đó, c 2 = a 2 + b 2 (tam giác vuông).
Ví dụ 3
Phân loại một tam giác có độ dài các cạnh là; 11 in, 13 in và 17 in.
Giải
a 2 + b 2 = 11 2 + 13 2 = 121 + 169 = 290
c 2 = 17 2 = 289
So sánh: 289 <290
Do đó, c 2 <a 2 + b 2 (tam giác nhọn)
Công thức Định lý Pythagoras được đưa ra là:
⇒ c 2 = a 2 + b 2
Ở đâu;
c = Chiều dài cạnh huyền;
a = chiều dài của một cạnh;
b = chiều dài của cạnh thứ hai.
Công thức này có thể được sử dụng để giải các bài toán khác nhau liên quan đến tam giác vuông. Ví dụ, chúng ta có thể sử dụng công thức để xác định độ dài thứ ba của một tam giác, khi độ dài hai cạnh của tam giác đã biết.
Các ví dụ làm việc của định lý Pythagoras:
Ví dụ 4
Hai cạnh ngắn của tam giác vuông là 5 cm và 12 cm. Tìm độ dài của cạnh thứ ba
Giải pháp
Cho trước, a = 5 cm
b = 12 cm
c =?
Từ công thức Định lý Pythagoras; c 2 = a 2 + b 2 , ta có;
c 2 = a 2 + b 2
c 2 = 12 2 + 5 2
c 2 = 144 + 25
√c 2 = √169
c = 13.
Do đó, cạnh thứ ba bằng 13 cm.
Ví dụ 5
Đường chéo và độ dài một cạnh của hình tam giác lần lượt là 25cm và 24cm. Kích thước của mặt thứ ba là gì?
Giải pháp
Sử dụng Định lý Pythagoras,
c 2 = a 2 + b 2 .
Cho b = cạnh thứ ba
25 2 = 24 2 + b 2
625 = 576 + b 2
625 – 576 = 576 – 576 + b 2
49 = b 2
b 2 = 49
b = √49 = 7 cm
Ví dụ 6
Tìm kích thước của màn hình máy tính có kích thước là 8 inch và 14 inch.
Gợi ý: Đường chéo của màn hình là kích thước của nó .
Giải pháp
Kích thước của màn hình máy tính giống như đường chéo của màn hình.
Sử dụng Định lý Pythagoras,
c 2 = 8 2 + 15 2
Giải quyết cho c.
c 2 = 64 + 225
c 2 = 289
c = √289
c = 17
Do đó, kích thước của màn hình máy tính là 17 inch.
Ví dụ 7
Tìm diện tích của một tam giác vuông, với đường chéo đó và đáy lần lượt là 8,5 cm và 7,7 cm.
Giải pháp
Sử dụng Định lý Pythagoras,
8,5 2 = a 2 + 7,5 2
Giải quyết cho a.
72,25 = a 2 + 56,25
72,25 – 56,25 = k 2 + 56,25 – 56,25
16 = a 2
a = √16 = 4 cm
Diện tích tam giác vuông = (½) x đáy x chiều cao
= (½ x 7,7 x 4) cm 2
= 15,4 cm 2
Ví dụ 8:
Nếu cạnh huyền của một tam giác vuông là 25 mm và chiều cao của nó nhỏ hơn 17 mm, hãy tìm đáy và chiều cao.
Giải pháp:
Áp dụng định lý Pitago
⇒ (x – 17) 2 + x 2 = 25 2
Đơn giản hóa.
⇒ x 2 – 2 (x) (17) + 17 2 + x 2 = 625
⇒ x 2 – 34x + 289 + x 2 = 625
⇒ 2x 2 – 34x + 289 = 625
⇒ 2x 2 – 34x – 336 = 0
⇒ x 2 – 17x – 168 = 0
⇒ (x + 7) (x – 24) = 0
⇒ x + 7 = 0
hoặc là
⇒ x – 24 = 0
⇒ x = -7, 24
Vì độ dài không được âm nên
⇒ x – 17 = 7
Do đó, cơ sở là 24 mm và chiều cao, là 7 mm.
Câu hỏi thực hành