Tam giác đồng dư và những ví dụ đơn giản nhất

Bạn phải hiểu rõ về máy photocopy. Khi bạn đặt một trang A4 vào bên trong máy và kích hoạt nó, bạn sẽ nhận được một bản sao y hệt của trang đó. Nếu bạn xoay hoặc lật trang, nó sẽ vẫn giống như trang gốc. Ngay cả khi bạn cắt chúng ra, bạn có thể xếp chúng lại một cách dễ dàng. Chúng tôi có thể nói các trang tương tự nhau hoặc đồng dư.

Hơn nữa, trang A4 có dạng hình chữ nhật nên khi bạn cắt nó theo đường chéo, bạn sẽ được hình tam giác. Nếu bạn cắt cả hai bản sao theo cùng một cách, bạn sẽ thấy cả hai bản sao sẽ tạo thành cùng một loại tam giác, có các góc và các cạnh bằng nhau.

Tam giác đồng dư là gì?

Đến đây chắc hẳn bạn đã biết rõ về một hình tam giác rằng nó là một hình 2 chiều có ba cạnh, ba góc và ba đỉnh. Hai hoặc nhiều tam giác được cho là đồng dư nếu các cạnh hoặc góc tương ứng của chúng là cạnh. Nói cách khác, tam giác đồng dạng có cùng hình dạng và kích thước .

Congruency là một thuật ngữ dùng để mô tả hai đối tượng có hình dạng và kích thước giống nhau . Biểu tượng cho sự đồng dư là ≅ . Trong hình tam giác, chúng tôi sử dụng chữ viết tắt CPCT . để chỉ ra rằng các phần tương ứng của các tam giác đồng dư là giống nhau.

Công suất không được tính toán hay đo lường mà chỉ được xác định bằng cách kiểm tra trực quan. Các tam giác có thể trở thành đồng dư theo ba chuyển động khác nhau, đó là chuyển động quay, phản xạ và tịnh tiến.

Triangle Congruence là gì?

Đồng dư tam giác là các quy tắc hoặc phương pháp được sử dụng để chứng minh xem hai tam giác có đồng dư hay không. Hai hình tam giác được cho là đồng dư nếu và chỉ khi một trong số chúng có thể được tạo ra để chồng lên nhau để bao phủ chính xác nó.

Bốn tiêu chí này được sử dụng để kiểm tra sự đồng dư của tam giác bao gồm :

Side – Side – Side ( SSS ), Side – Angle – Side ( SAS ), Angle – Side – Angle ( ASA ) và Angle – Angle – Side ( AAS ).

Ngoài ra còn có nhiều cách khác để chứng minh tính đồng dạng của tam giác, nhưng trong bài học này, chúng ta sẽ chỉ giới hạn trong các định đề này.

Trước khi đi vào chi tiết các định đề về sự đồng dư này , điều quan trọng là phải biết cách đánh dấu các mặt và góc khác nhau bằng một dấu hiệu nhất định cho thấy tính đồng dư của chúng. Bạn sẽ thường thấy các cạnh và góc của tam giác được đánh dấu bằng một chút dấu nhỏ để xác định tập hợp các góc đồng dư hoặc các cạnh đồng dư.

Bạn sẽ thấy trong sơ đồ bên dưới rằng các cạnh có một dấu tic có cùng số đo, các cạnh có hai dấu tic cũng có cùng độ dài và các cạnh có dấu tic cũng bằng nhau. Tương tự đối với các góc.

Bên – Góc – Bên

Góc cạnh bên (SAS) là một quy tắc được sử dụng để chứng minh xem một bộ tam giác đã cho có đồng dư hay không . Trong trường hợp này, hai tam giác đồng dạng nếu hai cạnh và một góc trong một tam giác đã cho bằng hai cạnh tương ứng và một góc trong tam giác khác.

Hãy nhớ rằng góc bao gồm phải được tạo bởi hai cạnh cho trước để các tam giác đồng dạng.

Hình minh họa quy tắc SAS:

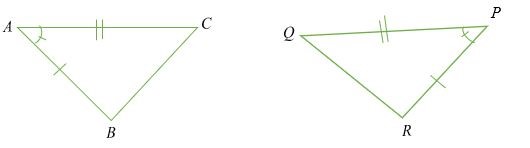
Cho rằng; độ dài AB = PR, AC = PQ và ∠ QPR = ∠ BAC , khi đó; Tam giác ABC và PQR đồng dư ( △ ABC ≅ △ PQR).

Góc – Góc – Bên

Quy tắc Góc – Góc – Cạnh (AAS) phát biểu rằng, hai tam giác đồng dạng nếu hai góc tương ứng và một cạnh không bao gồm của chúng bằng nhau.

Hình minh họa:

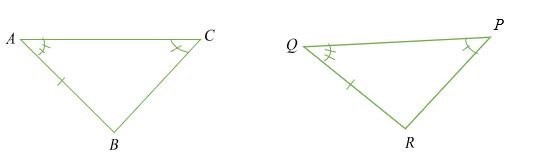
Cho rằng;

∠ BAC = ∠ QPR, ∠ AC B = ∠ RQP và chiều dài AB = QR, sau đó tam giác ABC và PQR là đồng dư ( △ ABC ≅ △ PQR).

Bên – Bên – Bên

Quy tắc cạnh bên (SSS) phát biểu rằng: Hai tam giác đồng dạng nếu độ dài ba cạnh tương ứng của chúng bằng nhau.

Hình minh họa:

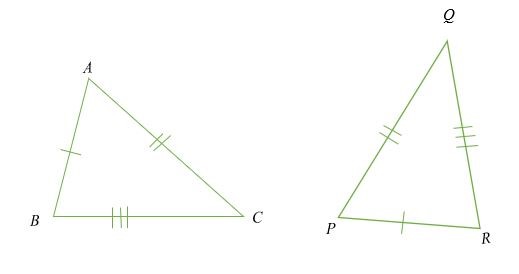
Tam giác ABC và PQR được cho là đồng dư ( △ ABC ≅ △ PQR) , nếu độ dài AB = PR , AC = QP và BC = QR .

Angle – Side – Angle

Quy tắc Góc – Cạnh – Góc (ASA) phát biểu rằng: Hai tam giác đồng dạng nếu hai góc tương ứng và một cạnh tương ứng của chúng bằng nhau.

Hình minh họa:

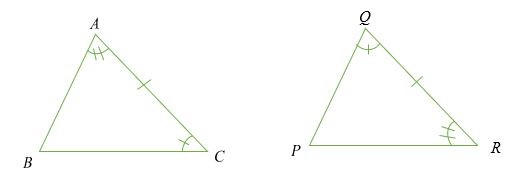
Tam giác ABC và PQR đồng dư ( △ ABC ≅ △ PQR) , nếu độ dài ∠ BAC = ∠ PRQ, ∠ ACB = ∠ PQR

Các ví dụ làm việc về đồng dư tam giác:

ví dụ 1

Hai tam giác ABC và PQR sao cho; AB = 3,5 cm, BC = 7,1 cm, AC = 5 cm, PQ = 7,1 cm, QR = 5 cm và PR = 3,5 cm. Kiểm tra xem các tam giác có đồng dư không.

Giải pháp

Cho: AB = PR = 3,5 cm

BC = PQ = 7,1 cm và

AC = QR = 5 cm

Do đó, ∆ABC ≅ ∆PQR (SSS)

Ví dụ 2

Cho biết ∠ ABC = (2x + 30) °, ∠ PQR = 55 ° và ∠ RPQ = 65 °, hãy tìm giá trị của x.

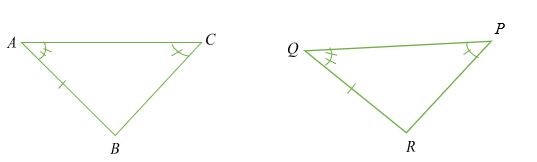
Giải pháp

ΔABC ≅ ΔPQR

Vì thế,

55 ° + 65 ° + (2x + 30) ° = 180 °

120 ° + 2x + 30 ° = 180 °

150 ° + 2x = 180 °

2x = 30 °

x = 15 °

Ví dụ 3

Mô tả dạng đồng dạng của hai tam giác cho bởi;

∆ ABC, AB = 7 cm, BC = 5 cm, ∠B = 50 ° và ∆ DEF, DE = 5 cm, EF = 7 cm, ∠E = 50 °

Giải pháp

Được:

AB = EF = 7 cm,

BC = DE = 5 cm và

∠B = ∠E = 50 °

Do đó, ∆ABC ≅ ∆FED (SAS)

Xem thêm:

Quy tắc Cosine và những cách giải hay nhất hiện nay

Quy tắc sin và những quy tắc tính toán vô cùng đơn giản

Ví dụ 4:

Chứng minh rằng tam giác ABC là tam giác cân, khi CP là đường cao và phân giác

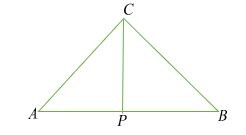
Giải:
Cho rằng độ dài cạnh AC ≅ BC thì,

Tam giác ABC cân.
Bây giờ, chúng ta hãy xem xét hai tam giác APC và BPC.

• ∠APC ≅ ∠CPB = 90 ° (CP là đường cao hoặc chiều cao của tam giác),
• ∠ACP ≅ ∠BCP (CP là đường phân giác)
• CP là mặt chung.
• △ APC ≅ △ BPC (Angle-Side-Angle)

Vì AC ≅ BC nên ABC là tam giác cân.

Ví dụ thực tế về các đối tượng đồng dư

Có vô số ví dụ về các đối tượng đồng dư mà chúng ta nhìn thấy hoặc quan sát được trong cuộc sống hàng ngày của chúng ta. Một ví dụ đơn giản là một gói bánh quy có tất cả các bánh quy có cùng kích thước và hình dạng, nếu chúng không bị vỡ. Có thể nói tất cả các loại bánh quy đều đồng dư.

Một vài ví dụ khác về sự đồng dư là:

• Hoa tai cùng bộ.
• Thuốc lá trong một gói.
• Bánh xe đạp.
• Các trang của một cuốn sách cụ thể.
• Các ngón tay út của cả hai bàn tay. Các ngón tay và ngón cái khác cũng đồng dạng. Nhiều cơ quan trong cơ thể của bạn, như thận và phổi đều hoạt động bình thường. Ngay cả khi một cơ thể bị cắt theo chiều dọc từ tâm thành hai nửa, thì cả hai nửa đều đồng dư.

Vấn đề thực hành

1. Các dạng khác nhau của đồng dư tam giác là gì?
2. Đúng hay sai: HL có thể được sử dụng để chứng minh tính đồng dư của tam giác.
3. ≅∆’s hay CPCTC là gì?
4. Đúng hay sai: (AAA) có thể được sử dụng để chứng minh tính đồng dư của tam giác.
5. Hai góc của một tam giác cân là 47 °. Tìm số đo của góc thứ ba.