Contents
Bộ ba Pythagore là gì?
Các nghiệm nguyên của Định lý Pitago , a 2 + b 2 = c 2 được gọi là Bộ ba Pitago chứa ba số nguyên dương a, b và c.
Ví dụ: (3, 4, 5)
Bằng cách đánh giá, chúng tôi nhận được:
3 2 + 4 2 = 5 2
9 + 16 = 25
Do đó, 3,4 và 5 là bộ ba của Pitago.
Bạn có thể nói “sinh ba”, nhưng “bộ ba” là thuật ngữ được ưa chuộng. Hãy bắt đầu chủ đề này bằng phần giới thiệu định lý Pythagoras.
Bàn
| (3, 4, 5) | (5, 12, 13) | (8, 15, 17) | (7, 24, 25) |
| (20, 21, 29) | (12, 35, 37) | (9, 40, 41) | (28, 45, 53) |
| (11, 60, 61) | (16, 63, 65) | (33, 56, 65) | (48, 55, 73) |
| (13, 84, 85) | (36, 77, 85) | (39, 80, 89) | (65, 72, 97) |
Công thức bộ ba Pythagoras
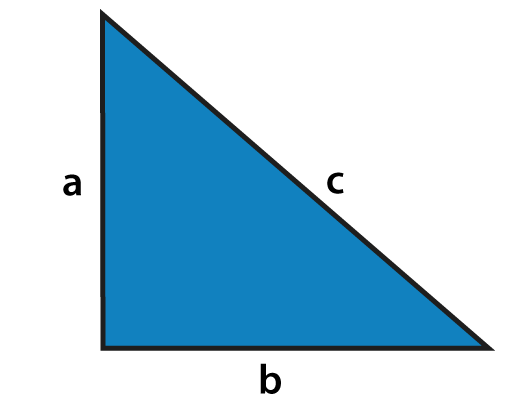
Nếu một tam giác có một góc là góc vuông (tức là 90 o ) thì tồn tại mối quan hệ giữa ba cạnh của tam giác.
Nếu cạnh dài nhất (được gọi là cạnh huyền) là r và hai cạnh còn lại (cạnh góc vuông) được gọi là p và q , thì:
p 2 + q 2 = r 2 .
hoặc là,
Tổng bình phương của hai cạnh còn lại bằng bình phương của cạnh dài nhất.
Danh sách bộ ba Pythagore
Dưới đây là danh sách các bộ ba Pitago trong đó giá trị của c trên 100:
| (20, 99, 101) | (60, 91, 109) | (15, 112, 113) | (44, 117, 125) |
| (88, 105, 137) | (17, 144, 145) | (24, 143, 145) | (51, 140, 149) |
| (85, 132, 157) | (119, 120, 169) | (52, 165, 173) | (19, 180, 181) |
| (57, 176, 185) | (104, 153, 185) | (95, 168, 193) | (28, 195, 197) |
| (84, 187, 205) | (133, 156, 205) | (21, 220, 221) | (140, 171, 221) |
| (60, 221, 229) | (105, 208, 233) | (120, 209, 241) | (32, 255, 257) |
| (23, 264, 265) | (96, 247, 265) | (69, 260, 269) | (115, 252, 277) |
Học sinh có thể chọn bất kỳ bộ ba nào từ danh sách trên và chứng minh công thức Pythagoras, tức là,
a 2 + b 2 = c 2
Làm thế nào để Tìm bộ ba Pitago?
Các quy tắc này như sau:
- Mọi số lẻ là cạnh p của bộ ba Pitago.
- Cạnh q của một bộ ba Pitago đơn giản là (p 2 – 1) / 2.
Bây giờ, p và r luôn luôn là số lẻ; q là chẵn.
- Các mối quan hệ này đúng vì hiệu giữa các số bình phương liên tiếp là các số lẻ liên tiếp.
- Tất cả các số lẻ tự nó là một bình phương (và bình phương của tất cả các số lẻ tự nó là một số lẻ) do đó cho ra một bộ ba Pitago.
Chứng minh bộ ba Pythagore
Chứng minh định lý Pythagoras:

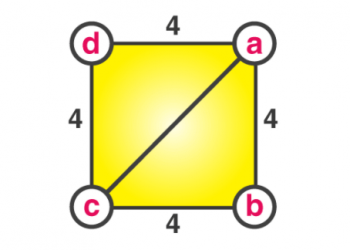
Nhìn vào hình trên
Trong hình bên trái,
Diện tích hình vuông = (a + b) 2
Diện tích tam giác = 1/2 (ab)
Diện tích hình vuông bên trong = b 2 .
Diện tích toàn bộ hình vuông = 4 (1/2 (ab)) + c 2
Bây giờ chúng ta có thể kết luận rằng
(a + b) 2 = 4 (1/2 (ab)) + c 2 .
hoặc là
a 2 + 2ab + b 2 = 2ab + c 2 .
Đơn giản hóa, chúng tôi nhận được công thức nhân ba số Pitago ,
a 2 + b 2 = c 2
Do đó đã được chứng minh.
Số hình tam giác
Sự khác biệt giữa các hình vuông liên tiếp là các số lẻ liên tiếp là một thực tế và gợi ý rằng mọi hình vuông là tổng của hai số tam giác liên tiếp .
Và trong điều này, các số tam giác là tổng liên tiếp của tất cả các số nguyên.
- 0 + 1 = 1 ,
- 0 + 1 + 2 = 3 ,
- 0 + 1 + 2 + 3 = 6 , v.v.
Vì vậy, các số hình tam giác là 1, 3, 6, 10, 15, 21, 28, 36, 45, 55, 66, 78, 91, 105, 120, v.v.
105 + 120 = 225 ; 225 là bình phương của 15.
Bộ ba Pythagore thường gặp
Như chúng ta đã biết, tập hợp cụ thể các số nguyên thỏa mãn định lý Pythagoras được gọi là bộ ba Pitago. Nó có nghĩa là tập hợp các số nguyên có mối liên hệ đặc biệt với định lý Pythagoras. Không chỉ tập hợp thỏa mãn định lý Pythagoras mà cả bội của tập hợp số nguyên cũng thỏa mãn định lý Pythagoras.
Ví dụ, (3, 4, 5) là bộ ba phổ biến nhất của Pitago. Khi mỗi số nguyên được nhân với 2, chúng ta nhận được tập (6, 8, 10), cũng thỏa mãn định lý Pythagoras.
(tức là,) 3 2 + 4 2 = 5 2
9 + 16 = 25
25 = 25
Tương tự, 6 2 + 8 2 = 10 2
36 + 64 = 100
100 = 100
Điều này có thể được diễn đạt đơn giản như sau:
Nếu a, b và c là các số nguyên dương thỏa mãn định lý Pythagoras thì ak, bk, ck cũng thỏa mãn định lý Pythagoras khi “k” là một số nguyên dương.
Ngoài ra, bộ ba Pitago có thể được tìm thấy bằng cách sử dụng các phương pháp khác nhau, chẳng hạn như dãy Fibonacci tổng quát, phương trình bậc hai, sử dụng ma trận và các phép biến đổi tuyến tính, v.v. Bộ ba số Pythagore là vô tận. Chúng ta có thể chứng minh rằng chúng ta có vô số bộ ba Pitago với sự trợ giúp của (3, 4, 5)
Dữ kiện: Một sự thật thú vị về bộ ba số Pitago là bộ ba số Pitago luôn bao gồm tất cả các số chẵn hoặc hai số lẻ và một số chẵn.
Một bộ ba Pitago không bao giờ được tạo thành từ tất cả các số lẻ hoặc hai số chẵn và một số lẻ
| Bộ ba Pythagore | x 2 (Lần 2) | x 3 (Lần 3) | x 4 (Lần 4) |
| 3-4-5 | 6-8-10 | 9-12-15 | 12-16-20 |
| 5-12-13 | 10-24-26 | 15-36-39 | 20-48-52 |
| 7-24-25 | 14-48-50 | 21-72-75 | 28-96-100 |
| 9-40-41 | 18-80-82 | 27-120-123 | 36-160-164 |
| 11-60-61 | 22-120-122 | 33-180-183 | 44-240-244 |
Ví dụ về bộ ba Pythagore (Có câu trả lời)
- Vì vậy, bình phương của 3, 9, là hiệu giữa 16, bình phương của 4 và 25 bình phương của 5, cho chúng ta bộ ba 7,24,25 .
- Tương tự, bình phương của 5, 25 là hiệu giữa 144, bình phương của 12 và 169, bình phương của 13, cho chúng ta bộ ba 5, 12, 13.
Các vấn đề về bộ ba Pythagore
Ví dụ 1:
Chứng minh rằng (5, 12, 13) là một bộ ba Pitago?
Giải pháp:
Để chứng minh: (5, 12, 13) là một bộ ba Pitago
Chúng ta biết rằng, a 2 + b 2 = c 2
(a, b, c) = (5, 12, 13)
Bây giờ, hãy thay thế các giá trị,
5 2 + 12 2 = 13 2
25 + 144 = 169
169 = 169
Do đó, tập hợp các số nguyên đã cho thỏa mãn định lý Pythagoras, (5, 12, 13) là một bộ ba Pitago.
Ví dụ 2:
Kiểm tra xem (7, 15, 17) có phải là bộ ba Pitago hay không.
Giải pháp:
(a, b, c) = (7, 15, 17)
Chúng ta biết rằng a 2 + b 2 = c 2
Bằng cách thay thế các giá trị trong phương trình, chúng ta nhận được
7 2 + 15 2 = 17 2
49 + 225 = 289
274 ≠ 289
Do đó, tập hợp các số nguyên đã cho không thỏa mãn định lý Pythagoras, (7, 15, 17) không phải là một bộ ba Pitago. Ngoài ra, nó chứng minh rằng bộ ba Pitago không được tạo thành từ tất cả các số lẻ.
Câu hỏi thường gặp – Câu hỏi thường gặp
Bộ ba Pitago là gì?
Năm bộ ba Pythagore phổ biến nhất là gì?
(5,12,13)
(7,24,25)
(9,40,41)
(11,60,61)
Làm thế nào để tìm bộ ba Pitago?
Mỗi số lẻ là cạnh p của bộ ba Pitago.
Cạnh q của một bộ ba Pitago đơn giản là (p 2 – 1) / 2.
Cạnh r là (q 2 + 1) / 2.
Nếu p = 9
q = (9 2 -1) / 2 = (81-1) / 2 = 80/2 = 40
r = (9 2 +1) / 2 = (81 + 1) / 2 = 82/2 = 41
Do đó, (9,40,41) là bộ ba số Pythagoras.
Làm thế nào để mở rộng quy mô của bộ ba?
(6,8,10)
Vậy, 6 2 +8 2 = 10 2
36 + 64 = 100
100 = 100
(4,5,8) có phải là bộ ba Pitago không?
Trước hết ta lấy LHS,
4 2 +5 2 = 16 + 25 = 41
RHS = 82 = 64
Rõ ràng, 41 không bằng 64
Do đó (4,5,8) không phải là bộ ba của Pitago.