Định lý Py-ta-go là gì? Xem xong 5 phút hiểu luôn.

Thất giác là gì? Xem xong 5 phút hiểu luôn.

Phát biểu định lý Pythagoras

Định lý Pythagoras phát biểu rằng ” Trong một tam giác vuông, bình phương của cạnh huyền bằng tổng bình phương của hai cạnh còn lại “. Các cạnh của tam giác này được đặt tên là Vuông góc, Cơ sở và Hạ vị. Ở đây, cạnh huyền là cạnh dài nhất, vì nó đối diện với góc 90 °. Các cạnh của một tam giác vuông (ví dụ a, b và c) có giá trị nguyên dương, khi được bình phương, được đưa vào một phương trình, còn được gọi là bộ ba Pitago.

Lịch sử

Định lý được đặt theo tên của một nhà Toán học người Hy Lạp tên là Pythagoras.

Công thức Định lý Pythagoras

Xét tam giác đã cho ở trên:

Trong đó “a” là đường vuông góc,

“B” là cơ sở,

“C” là cạnh huyền.

Theo định nghĩa, công thức Định lý Pythagoras được đưa ra là:

Cạnh đối diện với góc vuông (90 °) là cạnh dài nhất (được gọi là Hypotenuse) vì cạnh đối diện với góc lớn nhất là cạnh dài nhất.

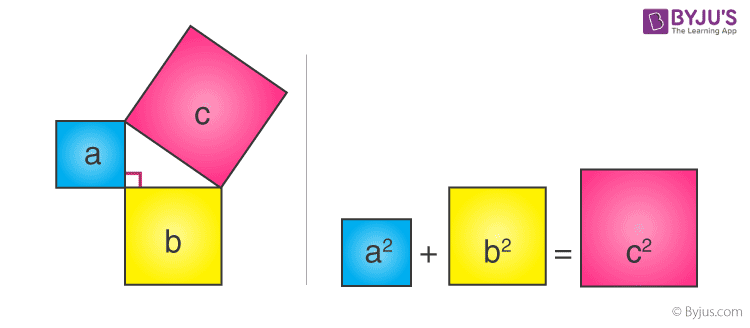
Xét ba hình vuông cạnh a, b, c gắn trên ba cạnh của một tam giác có các cạnh như hình vẽ bên.

Theo Định lý Pythagoras –

Diện tích hình vuông “a” + Diện tích hình vuông “b” = Diện tích hình vuông “c”

Thí dụ

Dưới đây là các ví dụ về định lý và dựa trên phát biểu cho tam giác vuông:

Xét một tam giác vuông, cho dưới đây:

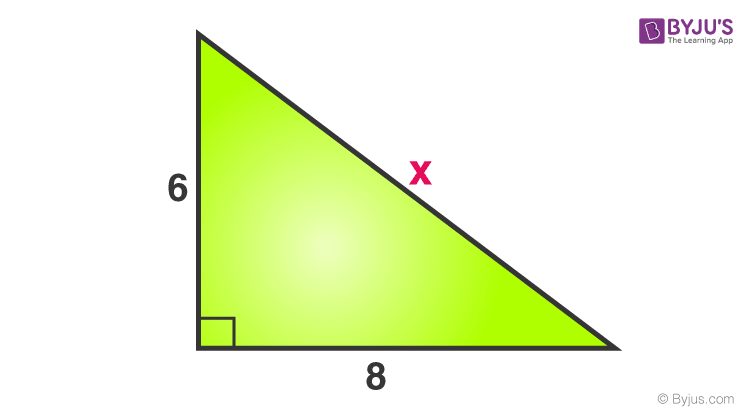
Tìm giá trị của x.

X là cạnh đối diện với góc vuông nên nó là cạnh huyền.

Bây giờ, theo định lý chúng ta biết;

Hypotenuse ²  = Cơ số ² + Vuông góc ²

x ² = 8 ² + 6 ²

x ² = 64 + 36 = 100

x = √100 = 10

Do đó, giá trị của x là 10.

Chứng minh Định lý Pythagoras

Cho: Tam giác vuông ABC, vuông cân tại B.

Để chứng minh- AC ² = AB ² + BC ²

Cách dựng: Vẽ BD vuông góc với AC tại D.

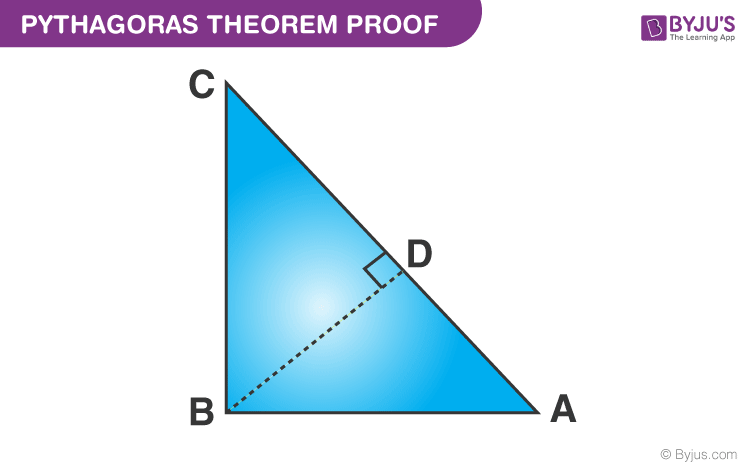
Bằng chứng:

Chúng tôi biết, △ ADB ~ △ ABC

Vì thế, A DA B=A BA C (các cạnh tương ứng của các tam giác đồng dạng)

Hoặc AB ²  = AD × AC …………………………… .. …… .. (1)

Ngoài ra, △ BDC ~ △ ABC

Vì thế, CDB C=B CA C (các cạnh tương ứng của các tam giác đồng dạng)

Hoặc, BC ² = CD × AC ……………………………… …… .. (2)

Cộng các phương trình (1) và (2) chúng ta nhận được,

AB ²  + BC ²  = AD × AC + CD × AC

AB ²  + BC ²  = AC (AD + CD)

Vì AD + CD = AC

Do đó, AC ² = AB ² + BC ²

Do đó, định lý Pitago được chứng minh.

Các ứng dụng của Định lý Pythagoras

• Để biết tam giác đó có phải là tam giác vuông cân hay không.
• Trong một tam giác vuông, chúng ta có thể tính độ dài của một cạnh bất kỳ nếu hai cạnh còn lại cho trước.
• Để tìm đường chéo của một hình vuông.

Hữu ích cho

Định lý Pythagoras rất hữu ích để tìm các cạnh của một tam giác vuông. Nếu chúng ta biết hai cạnh của một tam giác vuông, sau đó chúng ta có thể tìm thấy cạnh thứ ba.

Làm thế nào để sử dụng?

Để sử dụng định lý này, hãy nhớ công thức cho dưới đây:

c ² = a ²  + b ²

Trong đó a, b và c là các cạnh của tam giác vuông.

Ví dụ, nếu giá trị của a = 3 cm, b = 4 cm, thì hãy tìm giá trị của c.

Chúng tôi biết,

c ² = a ²  + b ²

c ² = 3 ² +4 ²

c ²  = 9 + 16

c ²  = 25

c = √25

c = 5

Do đó, cạnh thứ ba là 5 cm.

Như chúng ta thấy, a + b> c

3 + 4> 5

7> 5

Do đó, c = 5 cm là cạnh huyền của tam giác đã cho.

Làm thế nào để tìm một tam giác là một tam giác vuông?

Nếu chúng ta được cung cấp độ dài ba cạnh của một tam giác, thì để biết tam giác đó có phải là tam giác vuông hay không, chúng ta cần sử dụng định lý Pitago.

Hãy để chúng tôi hiểu tuyên bố này với sự trợ giúp của một ví dụ.

Giả sử một tam giác với các cạnh 10, 24 và 26 được cho.

Rõ ràng, 26 là cạnh dài nhất.

Nó cũng thỏa mãn điều kiện, 10 + 24> 26

Chúng tôi biết,

c ²  = a ²  + b ²     ……… (1)

Vì vậy, cho a = 10, b = 24 và c = 26

Đầu tiên, chúng ta sẽ giải quyết RHS của phương trình 1.

a ²  + b ² = 10 ²  + 24 ²  = 100 + 576 = 676

Bây giờ, lấy LHS, chúng tôi nhận được;

c ² = 26 ²  = 676

Chúng ta có thể nhìn thấy,

LHS = RHS

Do đó, tam giác đã cho là tam giác vuông, thỏa mãn định lý.

Các vấn đề về định lý Pitago

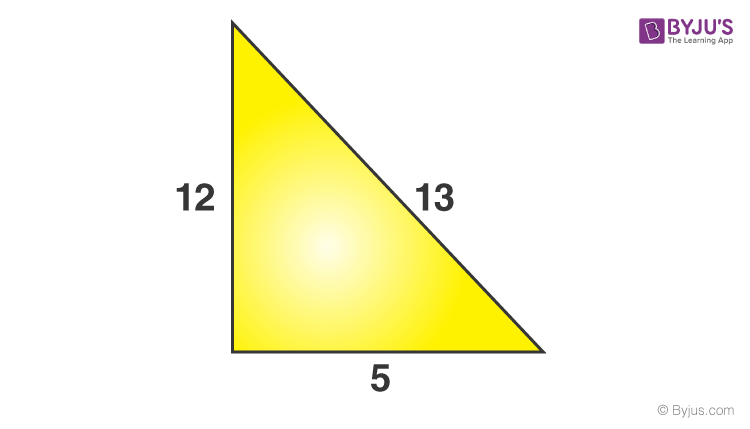
Bài toán 1:  Các cạnh của một tam giác là 5, 12 & 13 đơn vị. Kiểm tra xem nó có góc vuông hay không.

Lời giải: Từ Định lý Pythagoras, ta có;

Vuông góc ² + Cơ sở ² = Hypotenuse ²

Để cho,

Vuông góc = 12 đơn vị

Cơ sở = 5 đơn vị

Hypotenuse = 13 đơn vị {vì nó là số đo cạnh dài nhất}

12 ² + 5 ² = 13 ²

⇒ 144 + 25 = 169

⇒ 169 = 169 

LHS = RHS

Do đó, góc đối diện với cạnh 13 đơn vị sẽ là góc vuông.

Bài toán 2:  Hai cạnh của một tam giác vuông được cho như hình vẽ bên. Tìm mặt thứ ba.

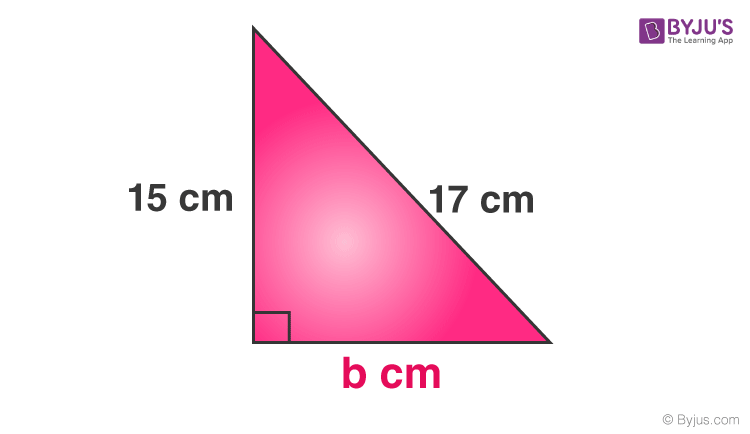
Vuông góc = 15 cm

Cơ sở = b cm

Hypotenuse = 17 cm

Theo Định lý Pitago, chúng ta có;

Vuông góc ² + Cơ sở ² = Hypotenuse ²

⇒15 ² + b ² = 17 ²

⇒225 + b ² = 289

⇒b ² = 289 – 225

⇒b ² = 64

⇒b = √64

Do đó,  b = 8 cm

Bài toán 3:  Cho cạnh của hình vuông là 4 cm. Tìm độ dài của đường chéo .

Lời  giải- Cho trước;

Các cạnh của hình vuông = 4 cm

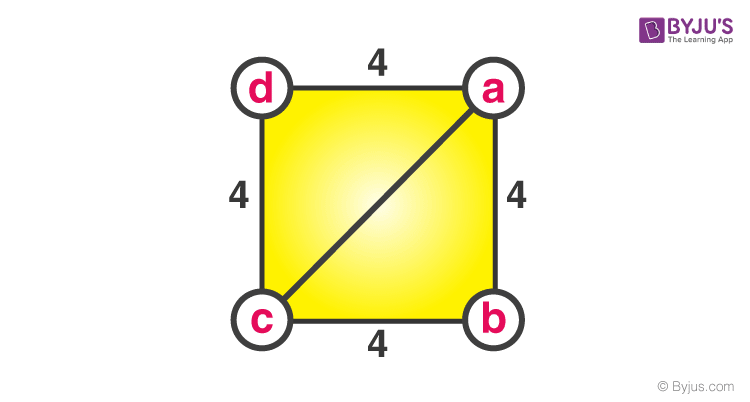
Để Tìm – Độ dài của đường chéo ac.

Xét tam giác abc (hoặc cũng có thể là acd)

(ab) ² + (bc) ²  = ( ac ) ²

(4) ² + (4) ² = (ac) ²

16 + 16 = (ac) ²

32 = (ac) ²

(ac) ² = 32

ac = 4√2.

Như vậy, độ dài của đường chéo là  4√2 cm.