Cách làm bộ phận tổng hợp đơn giản, dễ dàng chỉ vài nốt nhạc

Bộ phận Tổng hợp – Giải thích & Ví dụ

Đa thức là một biểu thức đại số được tạo thành từ hai hoặc nhiều số hạng bị trừ, cộng hoặc nhân. Một đa thức có thể chứa các hệ số, biến, số mũ, hằng số và các toán tử như phép cộng và phép trừ.

Cũng cần lưu ý rằng, một đa thức không thể có số mũ âm hoặc phân số. Ví dụ về đa thức là; 3y ²  + 2x + 5, x ³  + 2 x  ²  – 9 x – 4, 10 x  ³  + 5 x + y, 4x ²  – 5x + 7) v.v … Giống như số, đa thức có thể trải qua các phép cộng, trừ, nhân và sự phân chia.

Chúng ta đã thấy các phép tính cộng, trừ, nhân và chia dài của các đa thức trước đây, chúng ta hãy xem phép chia tổng hợp bây giờ.

Có hai phương pháp trong toán học để chia đa thức.

Đây là cách phân chia dài và phương pháp tổng hợp . Như tên cho thấy, phương pháp chia dài là quá trình phức tạp và đáng sợ nhất để làm chủ. Mặt khác, phương pháp tổng hợp là một cách “thú vị” để chia các đa thức.

Tôi phải nói rằng phép chia tổng hợp là một cách tắt để chia các đa thức vì nó đòi hỏi ít bước đi đến câu trả lời hơn so với phương pháp chia dài đa thức. Trong bài này, chúng ta sẽ tìm hiểu phương pháp chia tổng hợp là gì và cách thực hiện phương pháp này với một vài ví dụ.

Xem thêm:

Hướng dẫn cách chia đa thức hiệu quả nhất hiện nay

Cách cộng và Trừ đa thức như thế nào? Chi tiết cách thực hiện

Bộ phận tổng hợp là gì?

Phép chia tổng hợp có thể được định nghĩa là một cách viết tắt để chia một đa thức cho một đa thức bậc nhất khác. Phương pháp tổng hợp liên quan đến việc tìm các số 0 của đa thức.

Làm thế nào để làm bộ phận tổng hợp?

Để chia một đa thức bằng phép chia tổng hợp, bạn nên chia nó với một biểu thức tuyến tính có hệ số hàng đầu phải bằng 1.

Loại phép chia theo mẫu số tuyến tính này thường được gọi là phép chia theo  quy tắc Ruffini hoặc “phép tính trên giấy và bút chì ”.

Để có thể thực hiện được phương pháp phân chia tổng hợp, phải đáp ứng các yêu cầu sau:

• Số chia phải là một hệ số tuyến tính. Điều này có nghĩa là, ước số phải là một biểu thức của bậc 1.
• Hệ số đứng đầu của số chia cũng phải là 1. Nếu hệ số của số bị chia khác 1, quá trình chia tổng hợp sẽ rối tung lên. Do đó, bạn sẽ buộc phải thao tác với số chia để chuyển hệ số đứng đầu thành 1. Ví dụ, 4x – 1 và 4x + 9 sẽ lần lượt là x – ¼ và x + 9/4.

Để thực hiện phép chia tổng hợp đa thức, đây là các bước:

• Đặt số chia là 0 để tìm số cần đưa vào hộp chia.
• Biểu thị cổ tức ở dạng chuẩn. Điều này cũng giống như cách viết cổ tức theo thứ tự giảm dần. Nếu cổ tức thiếu một số điều khoản, hãy điền chúng bằng số không. Ví dụ: 3x ⁴+ 2 x ³ + 3x ² + 5 = 3x ⁴ + 2 x ³ + 3x ² + 0x +5
• Bây giờ, giảm hệ số hàng đầu trong cổ tức.
• Đặt vào cột trước tích của số bạn đưa xuống và số trong hộp chia.
• Ghi kết quả vào cuối hàng bằng cách thêm sản phẩm từ bước 4 và số đứng trước.
• Lặp lại quy trình 5 cho đến khi phần dư bằng 0 hoặc một giá trị số.
• Viết câu trả lời cuối cùng của bạn dưới dạng các số ở cột dưới cùng. Khi có một phần dư trong hộp chia, hãy biểu thị nó dưới dạng phân số với mẫu số là số chia.

LƯU Ý: Biến trong câu trả lời nhỏ hơn một lũy thừa so với cổ tức ban đầu

Bạn có thể thành thạo các bước trên bằng cách sử dụng câu thần chú sau: “Mang xuống, Nhân và cộng, nhân và cộng, Nhân và cộng,….”

ví dụ 1

Chia x ³  + 5x ²  -2x – 24 cho x – 2

Giải pháp

Thay đổi dấu của hằng số trong ước số x -2 từ -2 thành 2 và thả nó xuống.

_____________________
x – 2 | x ³ + 5x² – 2x – 24

2 | 1 5 -2 -24

Đồng thời hạ thấp hệ số hàng đầu. Điều này có nghĩa là 1 là số đầu tiên của thương.

2 | 1 5 -2 -24
________________________
1

Nhân 2 với 1 và thêm 5 vào tích để được 7. Bây giờ hạ 7 xuống.

2 | 1 5 -2 -24
2
________________________
1 7

Nhân 2 với 7 và thêm – 2 vào tích để được 12. Giảm 12

2 | 1 5 -2 -24
2 14
__________________________
1 7 12

Cuối cùng, nhân 2 với 12 và thêm -24 vào kết quả để nhận được 0.

2 | 1 5 -2 -24
2 14 24
__________________________
1 7 12 0

Vì thế;

x ³  + 5x ²  -2x – 24 / x – 2 = x² + 7x + 12

Ví dụ 2

Chia x ²  + 11x + 30 cho x + 5

Giải pháp

Thay đổi dấu của hằng số trong ước số x + 5 từ 5 thành -5 và hạ xuống.

_____________________
x ₊ 5 | x ²  + 11x + 30

-5 | 1 11 30

Giảm hệ số của số hạng đầu tiên trong cổ tức. Đây sẽ là thương số đầu tiên của chúng tôi

2 | 1 11 30
________________________
1

Nhân -5 với 1 và thêm 11 vào tích để được 6. Lấy 6 xuống;

-5 | 1 11 30
-5
________________________
1 6

Nhân -5 với 6 và thêm 30 vào kết quả để được 0.

-5 | 1 11 30
-5 -30
________________________
1 6 0

Do đó, thương là x + 6

Ví dụ 3

Chia 2x ³ + 5x ² + 9 cho x + 3

Giải pháp

Đảo ngược dấu của hằng số trong ước số x + 3 từ 3 thành -3 và đưa nó xuống dưới.

_____________________
x ₊ 3 | 2x ³  + 5x ² + 0x + 9

-3 | 2 5 0 9

Giảm hệ số của số hạng đầu tiên trong cổ tức. Đây sẽ là thương số đầu tiên của chúng tôi

-3 | 2 5 0 9
________________________
2

Nhân -3 với 2 và thêm 5 vào tích để được -1. Đưa -1 xuống;

-3 | 2 5 0 9
-6
________________________
2 -1

Nhân -3 với -1 và thêm 0 vào kết quả để được 3. Đưa 3 xuống.

-3 | 2 5 0 9
-6 3
________________________
2 -1 3

Nhân -3 với 3 và thêm -9 vào kết quả để được 0.

-3 | 2 5 0
9-6 3 -9
________________________
2 -1 3 0

Do đó, 2x ² – x + 3 là đáp án chính xác.

Ví dụ 4

Sử dụng bộ phận tổng hợp để phân chia 3 x ³ + 10x ² – 6x -20 bởi x + 2.

Giải pháp

Đảo ngược dấu của x + 2 từ 2 thành -2 và hạ nó xuống.

_____________________
x ₊ 2 | 4x ³ + 10x ² – 6x – 20

-2 | 4 10 6 20

Giảm hệ số của số hạng đầu tiên trong cổ tức.

-2 | 4 10 6 20
________________________
4

Nhân -2 với 4 và thêm 10 để được 2. Lấy 2 xuống;

-2 | 4 10 6 20
-8
________________________
4 2

Nhân -2 với 2 và thêm -6 vào kết quả để được 10. Đưa -10 xuống.

-2 | 4 10 -6
20-8 -4
________________________
4 2 10

Nhân -2 với 10 và thêm 20 vào kết quả để được 0.

-2 | 4 10 -6
20-8 -4 -20
________________________
4 2 -10 0

Do đó, 4x ² + 2x -10 là câu trả lời.

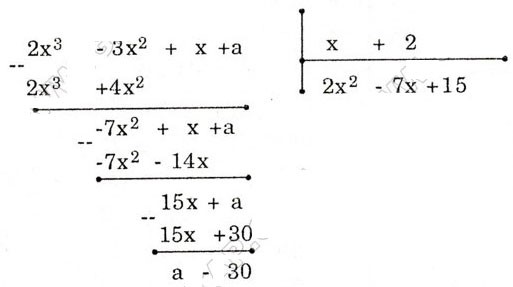
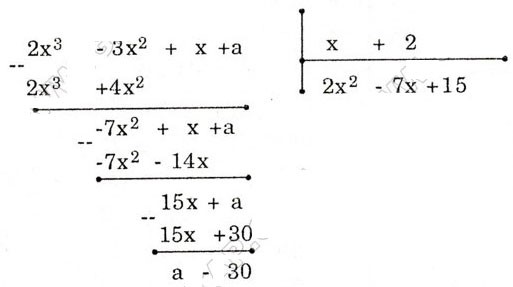
Ví dụ 5

Chia -9x ⁴ + 10x ³ + 7x ² – 6 bằng x-1.

Giải pháp

-9x ⁴ + 10x ³ + 7x ² – 6 / x-1 =

1 | -9 10 7 0 -6
-8 1 8 8
________________________
-9 8 8 2

Do đó, câu trả lời là -9x ³ + 8x ² + 8x + 2 / x -1

Câu hỏi thực hành

Sử dụng phép chia tổng hợp để chia các đa thức sau:

1. 2x ³ – 5x ² + 3x + 7 theo x -2
2. x ³ – 5x ² + 3x +7 theo x -3
3. 2x ³ + 5x ² + 9 theo x + 3
4. x ⁵ – 3x ³ – 4x – 1 x -1
5. – 2x ⁴ + x x x -3
6. – x ⁵ + 1 x + 1
7. 2x ³ – 13x ² + 17x – 10 theo x – 5
8. x ⁴ – 3x ³ – 11x ² + 5x + 17 theo x + 2
9. 4x ³ – 8x ² – x + 5 x 2x -1

Câu trả lời

1. 2x ² – x + 1 + 9 / x-2
2. x ² – 2x -2 -2 / x-3
3. 2x ² – x + 3 + 3 / x + 3
4. x ⁴ + x ³ – 2x ² – 2x – 7 / x-1
5. -2x ³ – 6x ² – 18x -53 – 159 / x-3
6. -x ⁴ + x ³ – x ² + x – 1 + 2 / x + 1
7. 2x ² – 3x + 2
8. x ³ – 5x ² – x + 7 + 3 / x + 2
9. 4x ² -6x -4 + 3 / (x – ½)