Các góc của một Hình bình hành, xem xong hiểu luôn.

Các góc của một Hình bình hành

Một tứ giác mà hai cặp cạnh đối của nó song song với nhau và bốn góc ở các đỉnh không bằng một góc vuông thì tứ giác đó được gọi là hình bình hành. Ngoài ra, các cạnh đối diện có chiều dài bằng nhau.

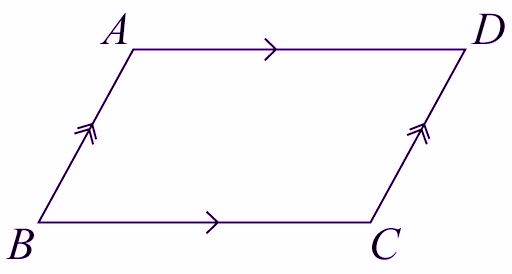
Đây,

AD = BC (cạnh đối diện)

AB = CD (các cạnh đối diện)

Tổng của tất cả bốn góc = 360 độ

Các tính chất quan trọng của các góc của hình bình hành là:

• Nếu một góc của hình bình hành là góc vuông thì tất cả các góc đều là góc vuông
• Các góc đối diện của một hình bình hành bằng nhau (hoặc đồng dư)
• Các góc liên tiếp là các góc bổ sung cho nhau (có nghĩa là chúng cộng lại tới 180 độ)

Đọc thêm:

Diện tích hình bình hành

Đường và góc lớp 7

Góc chuyển ngang đường song song

Chu vi của Hình bình hành

Các góc đối diện của một hình bình hành

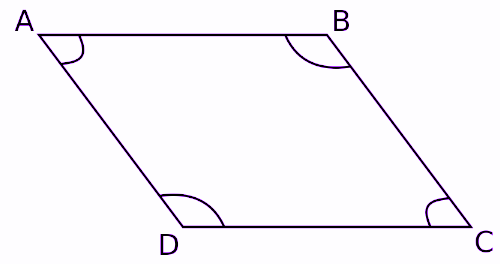
Trong hình bình hành trên, A, C và B, D là một cặp góc đối đỉnh.

Các góc đối diện của một hình bình hành bằng

Định lý: Chứng minh rằng các góc đối diện của hình bình hành bằng nhau.

Cho: Hình bình hành ABCD.

Để chứng minh: ∠B = ∠D và ∠A = ∠C

Bằng chứng:

Trong hình bình hành ABCD,

AB \\ CD và AD \\ BC

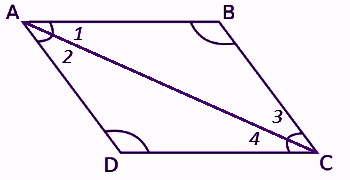
Xét tam giác ABC và tam giác ADC,

AC = AC (cạnh chung)

Chúng ta biết rằng các góc bên trong thay thế bằng nhau.

∠1 = ∠4

∠2 = ∠3

Theo tiêu chí đồng dư ASA, hai tam giác đồng dư với nhau.

Do đó, ∠B = ∠D và ∠A = ∠C

Do đó, người ta chứng minh rằng các góc đối diện của hình bình hành bằng nhau.

Các góc liên tiếp của một hình bình hành

Định lý: Chứng minh rằng mọi góc liên tiếp của hình bình hành là phụ.

Cho: Hình bình hành ABCD.

Để chứng minh: ∠A + ∠B = 180 độ, ∠C + ∠D = 180 độ

Bằng chứng:

AB ∥ CD và AD là một đối xứng.

Chúng ta biết rằng các góc bên trong ở cùng một phía của đường ngang là bổ sung.

Do đó, ∠A + ∠D = 180 °

Tương tự, ∠B + ∠C = 180 °, ∠C + ∠D = 180 ° và ∠A + ∠B = 180 °.

Do đó, tổng hai góc kề bất kỳ của hình bình hành bằng 180 °.

Do đó, chứng minh rằng hai góc kề hoặc góc liên tiếp của hình bình hành là phụ nhau.

Nếu một góc là góc vuông thì cả 4 góc đều là góc vuông:

Từ định lý trên, có thể quyết định rằng nếu một góc của hình bình hành là góc vuông (bằng 90 độ) thì cả bốn góc đều là góc vuông. Do đó, nó sẽ trở thành một hình chữ nhật.

Kể từ đó, các mặt liền kề là bổ sung.

Ví dụ, ∠A, ∠B là các góc kề nhau và ∠A = 90 °, thì:

∠A + ∠B = 180 °

90 ° + ∠B = 180 °

∠B = 180 ° – 90 °

∠B = 90 °

Tương tự, ∠C = ∠D = 90 °

Ví dụ 1:

Trong hình bên, ∠D = 85 ° và ∠B = (x + 25) °, hãy tìm giá trị của x.

Giải pháp:

Được,

∠D = 85 ° và ∠B = (x + 25) °

Chúng ta biết rằng, các góc đối diện của một hình bình hành là đồng dư hoặc bằng nhau.

Vì thế,

(x + 25) ° = 85 °

x = 85 ° -25 °

x = 60 °

Do đó, giá trị của x là 60.

Xem thêm:

• Ma trận nghịch đảo là gì? xem xong 5 phút hiểu luôn
• Biến đổi Laplace ngược là gì? xem xong 5 phút hiểu luôn
• Hàm ngược là gì? xem xong 5 phút hiểu luôn