Công thức cấp số cộng và các kiến thức đi kèm rễ học nhất

Bạn đang tìm hiểu những thông tin liên quan đến công thức cấp số cộng, câu hỏi đặt ra cấp số cộng là gì và đặc điểm tính chất của cấp số cộng như thế nào???

Để giải đáp những câu hỏi trên hôm nay tintuctuyensinh của chúng tôi sẽ cung cấp cho các bạn cái nhìn tổng quát nhất và các điểm các dạng bài tập liên quan đến công thức cấp số cộng. Từ đó là cơ sở quan trọng cho các bạn nghiên cứu học tập và lựa chọn cho mình phương pháp học tập hiệu quả để đạt thành tích cao nhất trong các kỳ thi

1. NHẬN THỨC CHUNG VỀ CÔNG THỨC CẤP SỐ CỘNG

Cấp số cộng là gì???

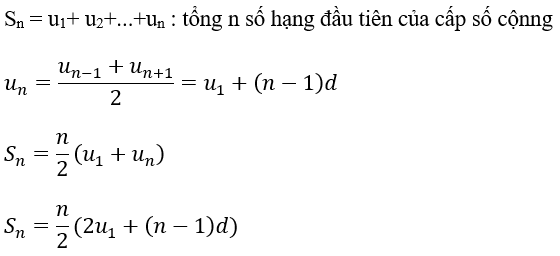
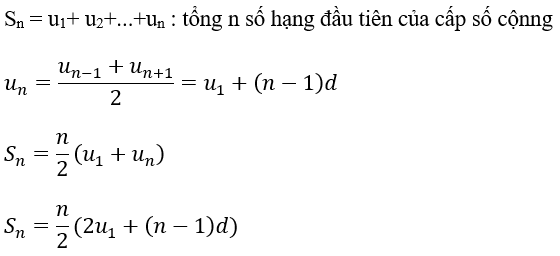
Trong chương trình trung học phổ thông ở môn Toán học chắc hẳn bạn được nghe tới khái niệm cấp số cộng cấp số nhân là gì nhưng để hiểu và xử lý tốt các bài toán liên quan đến cấp số cộng lại không dễ dàng. Bởi có thể nói đây là kiến thức không phải là nâng cao nhưng có rất nhiều bạn học sinh khi gặp các bài toán liên quan đến cấp số cộng lại khó xử lý và thường bỏ qua.

Để giúp bạn tự tin hơn khi gặp các bài toán này thì điều đầu tiên bạn cần phải nắm được đó là lý thuyết khái niệm cấp số cộng là gì?

Theo định nghĩa trong toán học: Cấp số cộng là một dãy số vô hạn hoặc hữu hạn, trong đó mỗi số hạng bắt đầu từ số hạng thứ hai của dãy số đều bằng tổng của số hạng đứng trước đó với một số được gọi là công sai không đổi.

Cụ thể nếu gọi Un là cấp số cộng thì kể từ số hạng thứ hai mỗi số hạng sau đều là trung bình cộng của hai số hạng đứng trước kế nó trong dãy số đó.

Ký hiệu: Cho cấp số cộng Un , nếu Un+1 = Un + d với n∈N∗, và d là hằng số.

Trong đó d là công sai  và bằng d = Un+1 – Un

Un là số hạng đầu tiên

Un+1 là số hạng tiếp theo kế tiếp số hạng Un

Ví dụ:

Cho dãy số 3; 9; 15; 21; 27; 33 là một cấp số cộng vì:

9 =3 + 6

15 = 9 + 6

21 = 15 + 6

27 = 21 + 6

33 = 27 + 6

Đây là Cấp số cộng có công sai d = 6 và số hạng đầu U1 = 3

Như vậy qua định nghĩa ở trên chúng ta đã hiểu được phần cơ bản về lý thuyết kiến thức về cấp số cộng, tiếp theo là phần các kiến thức, công thức liên quan đến cấp số cộng.

2. CÁC CÔNG THỨC CẤP SỐ CỘNG LIÊN QUAN 

Công thức cấp số cộng về số hạng tổng quát của cấp số cộng

Nếu cấp số cộng bắt đầu bằng số thứ tự a1 và có công sai d thì số hạng tiếp theo của cấp số cộng được tính theo công thức:

an = a1 + (n – 1)d

Ví dụ: Cho cấp số cộng (u2) trong đó u1`=−2, d = 3. Tìm u10 bằng bao nhiêu?

Áp dụng công thức về cấp số cộng ta có:

U10=u1+(10−1)d=u1 + 9d =−2 + 9.3 = 25

Vậy U10 bằng 25 là giá trị cần tìm.

Công thức cấp số cộng về n số hạng tổng quát

Giả sử cho cấp số cộng Un với mỗi số nguyên dương n thì tổng của n số hạng đầu tiên của dãy số là Sn = n(u1 + u2 + u3 + ….+ un) trong đó n ≥0

Ví dụ: Công ty A đang thực hiện việc trả lương cho các nhân viên của mình theo phương thức trả lương như sau: Mức lương của quý làm việc đầu tiên là 5 triệu đồng/quý và kể từ quý thứ 2 sẽ tăng lên 0,5 triệu đồng cho mỗi quý. Yêu cầu đặt ra hãy tính tổng tiền lương của một nhân viên nhận được sau 3 năm làm việc tại công ty A.

Bài giải:

Với mỗi số nguyên dương n, đặt Un (triệu đồng) là mức lương của nhân viên làm việc thứ n cho công ty A

Theo đề bài ta có:

U1= 5 ; un+1 =un + 0,5 với ∀n ≥ 1

Khi đó ta có dãy số (un) là một cấp số cộng với công sai d = 0,5

Do mỗi năm có 4 quý nên 3 năm sẽ có 12 quý.

Như vậy theo yêu cầu của đề bài ta cần phải tính tổng 12 số hạng đầu tiên của cấp số cộng (un)

Áp dụng công thức tính số hạng tổng quát ta được: u12= 5 +(12−1).0,5 = 10.5 

Áp dụng công thức tổng n số hạng đầu tiên ta được:

S12 = 12.(5 + 10,5) = 186 (triệu đồng)

Vậy tổng số tiền lương nhân viên nhận được sau 3 năm làm tại công ty là 186 triệu 

Tính chất của cấp số cộng

Với k≥2 ta có công thức tính chất của cấp số cộng như sau
Uk+1 + Uk−1 = 2Uk

Ví dụ:

Cho ba số lần lượt là 4;x;12 theo thứ đó tạo thành một cấp số cộng. Tìm x bằng bao nhiêu?

Giải: áp dụng công thức tính chất của cấp số cộng ta có:

Ta có: 2x=4 + 12=> x = 8 

Vậy x = 8 là giá trị cần tìm.Trên đây là toàn bộ những kiến thức liên quan đến công thức cấp số cộng và các dạng bài toán trọng tâm trong chương trình trung học phổ thông mà tintuctuyensinh của chúng tôi cung cấp cho các bạn tham khảo. Hy vọng công thức cấp số cộng là nguồn tài liệu hữu ích tạo cơ sở thuận lợi cho các bạn nghiên cứu và lựa chọn được phương pháp học tập khoa học hiệu quả.

Chúc các bạn sức khỏe và thành công!!

Xem thêm: 

Bí quyết thêm số mũ hiệu quả nhanh chóng nhất

Phép trừ các số mũ dễ hiểu, giải nhanh nhất 2021

Số mũ là gì? Những thông tin mới nhất về nó