|
Công thức Khoảng cách trong Toán học
Trong toán học, công thức khoảng cách được định nghĩa cho hình học tọa độ. Học sinh không nên nhầm lẫn ở đây đối với công thức về tốc độ và quãng đường. Cả hai hoàn toàn là hai chủ đề khác nhau. Khi chúng ta nói về tốc độ và khoảng cách, nó được đề cập trong các tình huống thực tế khi một người hoặc một phương tiện di chuyển với tốc độ để bao quát một khoảng cách trong một khoảng thời gian cụ thể. Khi đó tốc độ bằng tỷ số giữa quãng đường đi được và thời gian thực hiện.
Trong trường hợp hình học tọa độ, khi một người di chuyển từ điểm này đến điểm khác trong mặt phẳng, thì khoảng cách giữa điểm đầu và điểm cuối được tính bằng công thức khoảng cách. Hãy cùng chúng tôi tìm hiểu công thức của nó trong phần tiếp theo.
Công thức khoảng cách là gì?
Công thức khoảng cách là công thức, được sử dụng để tìm khoảng cách giữa hai điểm bất kỳ, chỉ khi chúng ta biết tọa độ. Các tọa độ này có thể nằm trong trục x hoặc trục y hoặc cả hai. Giả sử, có hai điểm, giả sử P và Q trong một mặt phẳng XY. Tọa độ của điểm P là (x 1 , y 1 ) và của Q là (x 2 , y 2 ). Khi đó công thức tìm khoảng cách giữa hai điểm PQ được cho bởi:
| PQ = √ [(x 2 – x 1 ) 2 + (y 2 – y 1 ) 2 ]
Hoặc là D = √ [(x 2 – x 1 ) 2 + (y 2 – y 1 ) 2 ] |
Trong đó D là khoảng cách giữa các điểm.
Công thức xác định khoảng cách
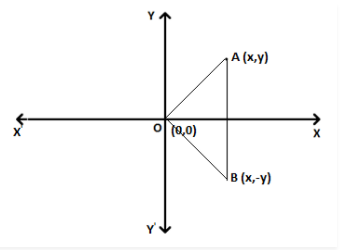
Gọi P (x 1 , y 1 ) và Q (x 2 , y 2 ) là tọa độ của hai điểm trên mặt phẳng tọa độ.


Vẽ hai đường thẳng song song với cả trục x và trục y (như hình vẽ bên) qua P và Q.
Đường thẳng song song qua P sẽ gặp đường vuông góc với trục x kẻ từ Q tại T.
Như vậy ΔPTQ vuông góc tại T.
PT = Cơ sở, QT = Vuông góc và PQ = Hypotenuse
Theo Định lý Pythagoras,
PQ 2 = PT 2 + QT 2
= (x 2 – x 1 ) 2 + (y 2 – y 1 ) 2
PQ = √ [(x 2 – x 1 ) 2 + (y 2 – y 1 ) 2 ]
Do đó, khoảng cách giữa hai điểm (x 1 , y 1 ) và (x 2 , y 2 ) là √ [(x 2 – x 1 ) 2 + (y 2 – y 1 ) 2 ]
Tương tự, khoảng cách của điểm P (x, y) từ gốc tọa độ O (0, 0) trong mặt phẳng Descartes được cho bởi công thức:
OP = √ (x 2 + y 2 )
Ví dụ về Công thức Khoảng cách
Hãy để chúng tôi giải quyết một số vấn đề dựa trên công thức khoảng cách.
Ví dụ 1: Tìm khoảng cách giữa hai điểm A (1, 2) và B (-2, 2).
Bài giải: Cho hai điểm A, B lần lượt có tọa độ (1, 2) và (-2, 2).
Cho A (1, 2) = (x 1 , y 1 )
B (-2, 2) = (x 2 , y 2 )
Để tìm: khoảng cách giữa A và B
Theo công thức khoảng cách giữa hai điểm ,
D = √ [(x 2 – x 1 ) 2 + (y 2 – y 1 ) 2 ]
AB = √ [(- 2 – 1) 2 + (2 – 2) 2 ]
AB = √ (-3) 2 + (0) 2
AB = √ 9 = 3 đơn vị.
Ví dụ 2: Chứng tỏ rằng các điểm (1, 7), (4, 2), (–1, –1) và (- 4, 4) là các đỉnh của một hình vuông.
Giải: Gọi P (1, 7), Q (4, 2), R (–1, –1) và S (- 4, 4) là tọa độ của bốn điểm trong mặt phẳng XY.
Để chứng minh: PQRS là hình vuông
Giải: Để chứng minh các điểm P, Q, R và S là một hình vuông, ta phải chứng minh rằng:
PQ = QR = RS = PS (Độ dài của hình vuông)
PR = QS (Đường chéo của hình vuông)
Bây giờ bằng công thức khoảng cách, chúng ta sẽ tìm khoảng cách giữa PQ, QR, RS, PS, PR và QS.
PQ = √ [(1 – 4) 2 + (7-2) 2 ] = √ (9 + 25) = √34
QR = √ [(4 + 1) 2 + (2 + 1) 2 ] = √ (25 + 9) = √34
RS = √ [(- 1+ 4) 2 + (–1 – 4) 2 ] = √ (9 + 25) = √34
PS = √ [(1 + 4) 2 + (7 – 4) 2 ] = √ (25 + 9) = √34
PR = √ [(1 + 1) 2 + (7 + 1) 2 ] = √ (4 + 64) = √68
QS = √ [(4 + 4) 2 + (2-4) 2 ] = √ (64 + 4) = √68
Vì PQ = QR = RS = PS và PR = QS.
Do đó, PQRS là một hình vuông.
Câu hỏi thường gặp – Câu hỏi thường gặp
Công thức cho khoảng cách là gì?
d = st
Ở đây,
d = Quãng đường
s = Tốc độ
t = Thời gian