Đa giác, Đường cong và Góc là gì? Xem xong 5 phút hiểu luôn.

Đường cong

Đường cong là một đường thẳng mượt mà bạn có thể vẽ trên giấy mà không cần dùng thước kẻ. Các đường ngẫu nhiên mà bạn vẽ nguệch ngoạc trên giấy cũng là các đường cong.

Có ba loại đường cong:

• Đường cong đơn giản: Đường cong không tự cắt nhau tại bất kỳ điểm nào. Trong hình, (i), (iii), (iv) và (vii) là các đường cong đơn giản.
• Đường cong mở: Đường cong có điểm cuối không gặp nhau. (i), (ii), (v) và (vi) là các đường cong mở.
• Đường cong kín: Đường cong bao quanh hoàn toàn một khu vực và không có điểm cuối. (iii), (iv) và (vii) là các đường cong mở.

Góc

Góc là độ nghiêng của hai tia ló ra khỏi một điểm chung. Điểm này được gọi là đỉnh của góc và hai tia tạo thành góc được gọi là cánh tay hoặc cạnh của nó.

Ghi chú:

• Nếu hai cánh tay tạo thành một góc 90 độ giữa chúng, nó được gọi là góc vuông.
• Nếu độ nghiêng giữa hai cánh tay nhỏ hơn góc vuông, nó được gọi là góc nhọn.
• Nếu độ nghiêng giữa các cánh tay hơn một góc vuông, nó được gọi là góc tù.

Trong hình sau:

• O là đỉnh của góc.
• OP và OQ là tia tạo thành góc. Chúng là các cạnh hoặc các nhánh của góc.
• Khi đặt tên cho một góc, đỉnh luôn được viết dưới dạng chữ cái ở giữa. Ở đây góc được viết là ∠POQ

Đa giác

Đa giác là một hình phẳng được bao bởi ba đoạn thẳng trở lên. Các đoạn thẳng được gọi là các cạnh của đa giác. Điểm mà hai đoạn thẳng gặp nhau được gọi là đỉnh của đa giác. Các cặp cạnh gặp nhau ở cùng một đỉnh được gọi là các cạnh kề nhau. Các điểm cuối của cùng một phía được gọi là các đỉnh kề nhau. Đoạn thẳng nối hai đỉnh không kề nhau của đa giác được gọi là đường chéo của đa giác.

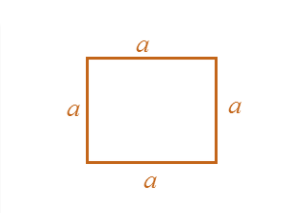
• Khi tất cả các cạnh có độ dài bằng nhau, đa giác được cho là đa giác đều. Ví dụ: hình vuông. Nếu không, nó là một đa giác không đều.
• Một tam giác là một đa giác có số cạnh tối thiểu là 3.
• Danh pháp của chúng được thực hiện trên cơ sở số lượng các cạnh mà chúng có. Đa giác có 3 cạnh được gọi là tam giác, 4 cạnh được gọi là tứ giác và 5 cạnh được gọi là ngũ giác, v.v.

Trong đa giác sau:

• AB, BC, CD, DE và EA là các cạnh
• A, B, C, D và E là các đỉnh
• AB và BC là các cạnh kề
• A và E là các đỉnh kề nhau. A và C không phải là đỉnh liền kề
• AD, AC, BE, BD và CE là các đường chéo

Xem thêm bài viết: 

• Điểm chuẩn học bạ Đại học Hạ Long đợt 1 năm 2021
• Thừa số nguyên tố là gì? Xem xong 5 phút hiểu luôn.
• Số nguyên tố, số tổng hợp và số chẵn số lẻ là gì? Xem xong 5 phút hiểu luôn.