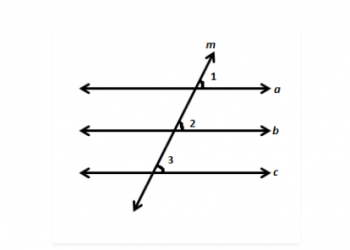
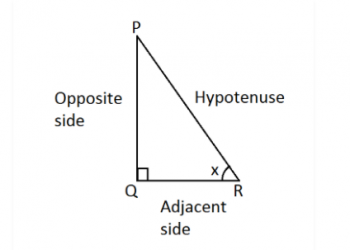
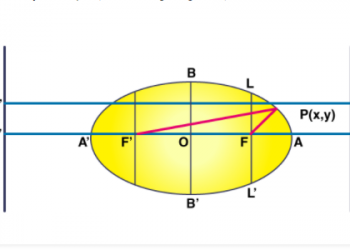
Tuyên bố và Chứng minh Luật của De Morgan
Một tập hợp các đối tượng hoặc phần tử được xác định rõ ràng được gọi là một tập hợp. Các phép toán khác nhau như phần bù của một tập hợp, liên hợp và giao điểm có thể được thực hiện trên hai tập hợp. Các thao tác này và cách sử dụng chúng có thể được đơn giản hóa hơn nữa bằng cách sử dụng một bộ luật được gọi là Luật De Morgan. Đây là những luật rất dễ dàng và đơn giản.
Bất kỳ tập hợp nào bao gồm tất cả các đối tượng hoặc phần tử liên quan đến một ngữ cảnh cụ thể được định nghĩa là một tập hợp phổ quát. Xét một tập phổ quát U sao cho A và B là các tập con của tập phổ quát này.
Theo định luật thứ nhất của De Morgan, phần bù của hợp của hai tập A và B bằng giao của phần bù của tập A và B.
(A∪B) ‘= A’∩ B’ —– (1)
Trong đó phần bổ sung của một tập hợp được định nghĩa là
A ‘= {x: x ∈ U và x ∉ A}
Trong đó A ‘biểu thị phần bù.
Có thể dễ dàng hình dung luật này bằng cách sử dụng Sơ đồ Venn.
LHS của phương trình 1 đại diện cho phần bù của sự kết hợp của hai tập hợp A và B. Trước hết, sự kết hợp của hai tập hợp A và B được định nghĩa là tập hợp của tất cả các phần tử nằm trong tập hợp A hoặc tập hợp B. Nó có thể được hình dung bằng cách sử dụng Biểu đồ Venn như được hiển thị:
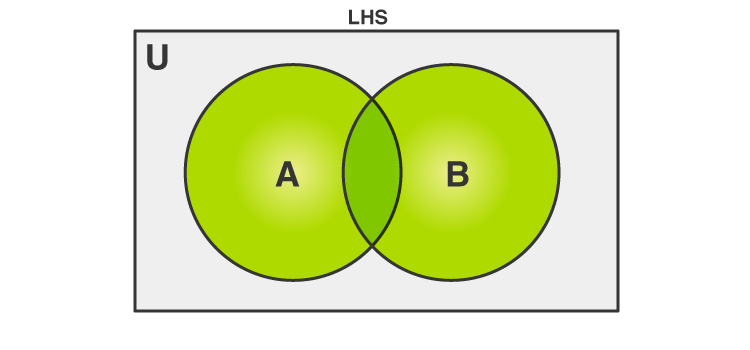

Hình 1 Liên hiệp các bộ
Phần được tô sáng hoặc màu xanh lục biểu thị A∪B. Phần bù của kết hợp A và B tức là, (A∪B) ‘là tập hợp của tất cả các phần tử không có trong A∪B. Có thể hình dung điều này như sau:
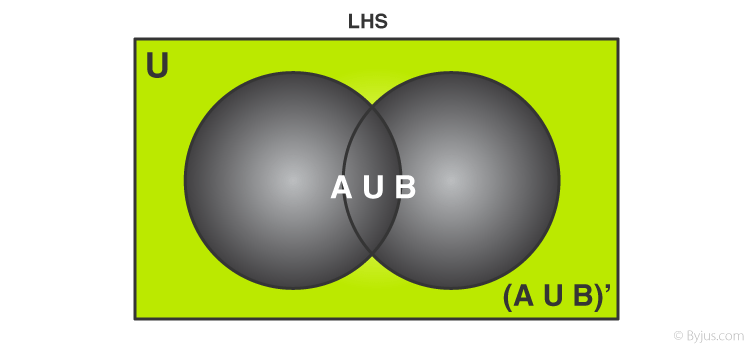

Hình 2 Sự bổ sung của các bộ
Tương tự, RHS của phương trình 1 cũng có thể được biểu diễn bằng cách sử dụng Biểu đồ Venn, phần đầu tiên, tức là, A ‘có thể được mô tả như sau:
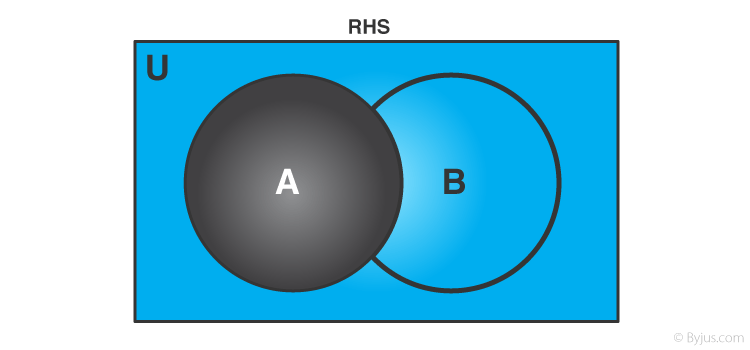

Hình 3 Sự bổ sung của bộ A
Phần màu đen biểu thị tập hợp A và phần màu xanh lam biểu thị phần bù của nó, tức là, A ‘.
Tương tự, B ‘được biểu diễn như sau:
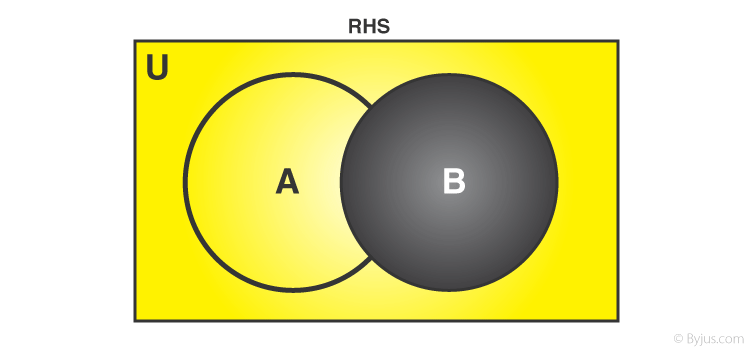

Hình 4 Sự bổ sung của bộ B
Phần màu đen biểu thị tập hợp B và phần màu vàng biểu thị phần bù của nó, tức là, B ‘.
Nếu hình. 3 và 4 được chồng lên nhau, ta được hình tương tự như phần bù của tập hợp.
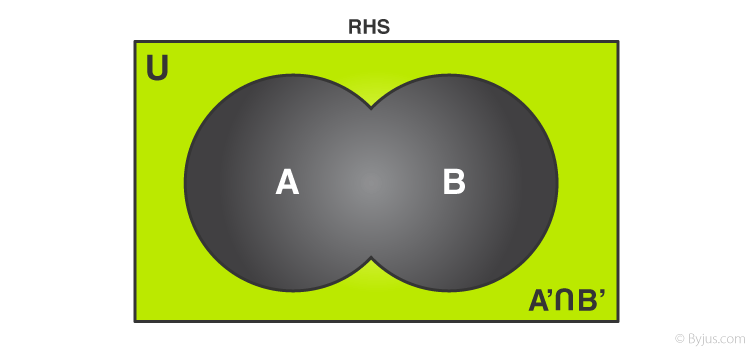

Hình 5 Giao điểm của các phần bổ sung của các tập hợp
Do đó LHS = RHS
Về mặt toán học,
Như, A∪B = hoặc trong A hoặc trong B
(A∪B) ‘= LHS = không ở A cũng không ở B
Ngoài ra, A ‘= Không có trong A
B ‘= Không có trong B
A’∩ B ‘= Không ở A và không ở B
⇒ (A∪B) ‘= A’∩ B’
Do đó, bằng cách hình dung Sơ đồ Venn và phân tích Định luật De Morgan bằng cách viết nó ra, giá trị của nó có thể được chứng minh.
Chúng tôi có thể áp dụng De Morgan lý t o phủ định một dis ngã ba hay sự phủ định của kết hợp trong toàn bộ hoặc một phần của một công thức. Định lý này giải thích rằng phần bù của tất cả các số hạng bằng tổng của phần bù của mỗi số hạng. Tương tự, phần bù của tổng tất cả các số hạng bằng tích của phần bù của mỗi số hạng. Ngoài ra, định lý này được sử dụng để giải các bài toán khác nhau trong đại số boolean.
Xanthogranuloma vị thành niên là gì? Những nguyên nhân, triệu chứng