Contents
Định lý giá trị trung bình của Lagrange
Nếu một hàm f được xác định trên khoảng đóng [a, b] thỏa mãn các điều kiện sau:
i) Hàm f liên tục trên khoảng đóng [a, b]
ii) Hàm f khả vi trên khoảng hở (a, b)
Khi đó, tồn tại một giá trị x = c sao cho
f ‘(c) = [ f (b) – f (a)] / (ba)
Định lý này còn được gọi là định lý giá trị trung bình đầu tiên hoặc định lý giá trị trung bình Lagrange .
Giải thích Hình học của Định lý Giá trị Trung bình của Lagrange


Trong đồ thị đã cho, đường cong y = f (x) liên tục từ x = a và x = b và phân biệt được trong khoảng đóng [a, b] thì theo định lý giá trị trung bình của Lagrange, đối với bất kỳ hàm nào liên tục trên [ a , b ] và khả vi trên ( a , b ) thì tồn tại một số c trong khoảng ( a , b ) sao cho đoạn nối các điểm cuối của khoảng [ a , b ] song song với tiếp tuyến tại c .
f′( c ) = f( b ) – f( a )b – a
Điều này có thể được hiểu theo cách tốt hơn với ví dụ được đưa ra dưới đây.
Thí dụ:
Kiểm định Định lý Giá trị Trung bình cho hàm f (x) = x 2 – 4x – 3 trong khoảng [a, b], trong đó a = 1 và b = 4.
Giải pháp:
Được,
f (x) = x 2 – 4x – 3
f ‘(x) = 2x – 4
a = 1 và b = 4 (đã cho)
f (a) = f (1) = (1) 2 – 4 (1) – 3 = 1 – 4 – 3 = -6
f (b) = f (4) = (4) 2 – 4 (4) – 3 = -3
Hiện nay,
[f (b) – f (a)] / (b – a) = (-3 + 6) / (4 – 1) = 3/3 = 1
Theo phát biểu định lý giá trị trung bình, có một điểm c ∈ (1, 4) sao cho f ‘(c) = [f (b) – f (a)] / (b – a), tức là f’ (c ) = 1.
2c – 4 = 1
2c = 5
c = 5/2 ∈ (1, 4)
Xác minh: f ‘(c) = 2 (5/2) – 4 = 5 – 4 = 1
Do đó, đã xác minh định lý giá trị trung bình.
Định lý Rolle
Một trường hợp đặc biệt của định lý giá trị trung bình của Lagrange là Định lý Rolle phát biểu rằng:
Nếu một hàm f được xác định trong khoảng đóng [a, b] sao cho nó thỏa mãn các điều kiện sau.
i) Hàm f liên tục trên khoảng đóng [a, b]
ii) Hàm f khả vi trên khoảng hở (a, b)
iii) Bây giờ nếu f (a) = f (b), thì tồn tại ít nhất một giá trị của x, chúng ta hãy giả sử giá trị này là c, nằm giữa a và b tức là (a <c <b) trong a sao cho f ‘(c) = 0.
Chính xác là, nếu một hàm số liên tục trên khoảng đóng [a, b] và khả vi trên khoảng mở (a, b) thì tồn tại điểm x = c trong (a, b) sao cho f ‘(c) = 0
Giải thích hình học của Định lý Rolle
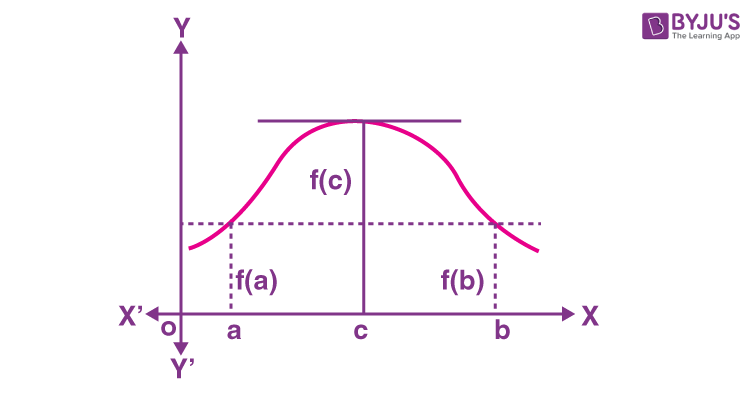

Trong đồ thị đã cho, đường cong y = f (x) liên tục giữa x = a và x = b và tại mọi điểm, trong khoảng đó, có thể vẽ tiếp tuyến và hoành độ tương ứng với hoành độ và bằng nhau. tồn tại ít nhất một tiếp tuyến của đường cong song song với trục x.
Về mặt đại số, định lý này cho chúng ta biết rằng nếu f (x) biểu diễn một hàm đa thức theo x và hai nghiệm nguyên của phương trình f (x) = 0 là x = a và x = b, thì tồn tại ít nhất một nghiệm nguyên của phương trình f ‘(x) = 0 nằm giữa các giá trị này.
Ngược lại của định lý Rolle là không đúng và cũng có thể tồn tại nhiều hơn một giá trị của x, mà định lý này đúng nhưng vẫn có xác suất tồn tại của một giá trị như vậy.
Phát biểu định lý Rolle
Về mặt toán học, định lý Rolle có thể được phát biểu như sau:
Cho f: [a, b] → R liên tục trên [a, b] và khả vi trên (a, b), sao cho f (a) = f (b), trong đó a và b là một số thực. Khi đó tồn tại một số c trong (a, b) sao cho f ′ (c) = 0.
Ví dụ về Định lý Rolle
Thí dụ:
Kiểm chứng định lý Rolle cho hàm số y = x 2 + 2, a = –2 và b = 2.
Giải pháp:
Từ định nghĩa của định lý Rolle, hàm số y = x 2 + 2 liên tục trong [- 2, 2] và khả vi trong (- 2, 2).
Từ cái đã cho,
f (x) = x 2 + 2
f (-2) = (-2) 2 + 2 = 4 + 2 = 6
f (2) = (2) 2 + 2 = 4 + 2 = 6
Do đó, f (- 2) = f (2) = 6
Do đó, giá trị của f (x) tại –2 và 2 trùng nhau.
Bây giờ, f ‘(x) = 2x
Định lý Rolle phát biểu rằng có một điểm c ∈ (- 2, 2) sao cho f ′ (c) = 0.
Tại c = 0, f ′ (c) = 2 (0) = 0, trong đó c = 0 ∈ (- 2, 2)
Do đó đã được xác minh.
Xem thêm: