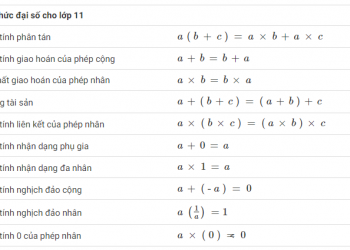
Trong đó Hypotenuse là cạnh đối diện với góc vuông (90 độ), Vuông góc là cạnh kề với góc vuông và nối với cạnh huyền, Cơ sở là cạnh kề với góc vuông, ở đây gọi là chân của tam giác. Với sự trợ giúp của công thức này, chúng ta có thể dễ dàng tìm độ dài cạnh của một tam giác vuông , nếu chúng ta biết độ dài của hai cạnh còn lại.
Tam giác này cũng có thể được đề cập là tam giác vuông. Ở đây, chỉ có một góc là 90 độ và tổng các tam giác khác bằng 90 độ, đó là các góc nhọn. Cơ sở và đường trung trực của tam giác vuông có thể hoán đổi cho nhau, tùy thuộc vào góc nhọn nào mà chúng ta đang xem xét. Ba cạnh, tức là cơ sở, vuông góc và cạnh huyền được gọi là bộ ba Pitago và nếu cả ba cạnh là số nguyên thì tam giác được gọi là tam giác Pitago .
Contents
Chứng minh Định lý Tam giác vuông góc
Định lý : Trong một tam giác, nếu bình phương của một cạnh bằng tổng bình phương của hai cạnh còn lại thì góc đối diện với cạnh thứ nhất là góc vuông.
Để chứng minh: ∠B = 90 °
Chứng minh: Ta có ∆ ABC trong đó AC 2 = A B 2 + BC 2
Chúng ta cần chứng minh rằng ∠B = 90 °
Để chứng minh điều trên, ta dựng tam giác P QR vuông tại Q sao cho:
PQ = AB và QR = BC
Từ tam giác PQR , ta có
PR 2 = PQ 2 + QR 2 (Theo định lý Pythagoras, Q = 90 ° )
hoặc, PR 2 = AB 2 + BC 2 (Theo cách xây dựng) …… (1)
Chúng ta biết rằng;
AC 2 = AB 2 + BC (Đã cho) ………… (2)
Vì vậy, AC = PR [Từ phương trình (1) và (2)]
Bây giờ, trong Δ ABC và Δ PQR ,
AB = PQ (Theo cách xây dựng)
BC = QR (Theo cách xây dựng)
AC = PR [Đã chứng minh ở trên]
Vì vậy, Δ ABC ≅ Δ PQR (Theo đồng dư SSS)
Do đó, ∠B = ∠Q (CPCT)
Nhưng, ∠Q = 90 ° (Theo cấu trúc)
Vì vậy, ∠B = 90 °
Do đó các định lý được chứng minh.
Công thức tam giác góc phải
Công thức tam giác vuông được cho bởi:
(Hypotenuse) 2 = (Cạnh kề) 2 + (Cạnh đối diện) 2
Nếu a, b và c vuông góc, đáy và cạnh huyền của tam giác vuông thì;
c 2 = a 2 + b 2
Hoặc chúng ta cũng có thể viết nó là;
c = √ (a 2 + b 2 )
Có nghĩa là cạnh huyền bằng căn của tổng bình phương của cơ sở và vuông góc.
Diện tích của một tam giác vuông bằng một nửa tích của đáy và đường cao hoặc vuông góc.
A = 1/2 bxh
trong đó b là cơ sở và h là độ dài vuông góc.
Các ví dụ
Q.1: Góc ∠PRQ = 90∘ và RS vuông góc với PQ. Chứng minh rằng QR 2 / PR 2 = Q S / PS .
Giải pháp: Chúng ta có thể thấy rằng;
△ PSR ~ △ PRQ
Theo tính chất của tam giác đồng dạng ta có:
PR / PQ = PS / PR
hoặc nó cũng có thể được viết là, PR 2 = PQ.PS ………. (1)
Tương tự, chúng ta có △ QSR ~ QRP
Vì vậy, chúng tôi có, QS / QR = QR / QP
Hoặc nó cũng có thể được viết là;
QR 2 = QP.QS ……… .. (2)
Bằng cách chia phương trình (2) cho (1), chúng ta có thể suy ra rằng:
QR 2 / PR 2 = ( QP.QS) / (PQ.PS) = Q S / PS
Do đó, đã chứng minh.
H.2: Nêu số đo cạnh huyền và cạnh đáy nếu 5cm và 3cm của tam giác vuông. Sau đó tìm chiều cao của nó.
Bài giải: Bằng công thức về góc vuông, ta biết;
(Hypotenuse) 2 = (Cạnh kề) 2 + (Cạnh đối diện) 2
(5) 2 = (3) 2 + (Vuông góc) 2
25 = 9 + (P) 2
16 = (P) 2
P = √16 = 4cm
Do đó, số đo của vuông góc là 4 cm
Xem thêm: