Cách học định lý Tam giác Sum hiệu quả nhất hiện nay

Định lý Tam giác Sum – Giải thích & Ví dụ

Chúng ta biết rằng các tam giác khác nhau có các số đo góc và độ dài cạnh khác nhau, nhưng có một điều cố định là mỗi tam giác được tạo bởi ba góc trong và ba cạnh có thể có cùng độ dài hoặc độ dài khác nhau.

Ví dụ, một tam giác vuông có một góc chính xác là 90 độ và hai góc nhọn.

Tam giác cân có hai góc bằng nhau và độ dài hai cạnh bằng nhau. Các tam giác đều có các góc và độ dài các cạnh bằng nhau.
Các tam giác Scalene có các góc khác nhau và độ dài các cạnh khác nhau.

Mặc dù thực tế là tất cả các tam giác này khác nhau về góc hoặc độ dài cạnh, nhưng tất cả chúng đều tuân theo các quy tắc và tính chất giống nhau.

Trong bài viết này, bạn sẽ tìm hiểu về:

• Định lý tổng tam giác,
• Các góc trong của một tam giác và
• Làm thế nào để sử dụng Định lý Tổng Tam giác để tìm các góc trong của một tam giác?

Góc trong của một tam giác là gì?

Trong hình học, các góc trong của một tam giác là các góc được tạo thành bên trong một tam giác.

Các góc trong có các tính chất sau:

• Tổng các góc trong là 180 độ (Định lý Tổng góc Tam giác).
• Tất cả các góc trong của một tam giác đều lớn hơn 0 ° nhưng nhỏ hơn 180 °.
• Các đường phân giác của cả ba góc trong cắt nhau bên trong một tam giác tại một điểm được gọi là tâm, là tâm của đường tròn nội tiếp của tam giác.
• Tổng của mỗi góc bên trong và góc bên ngoài bằng 180 ° (đường thẳng).

Định lý tổng góc tam giác là gì?

Một thuộc tính chung về hình tam giác là, cả ba góc nội thất cộng lại tối đa 180 độ. Điều này bây giờ đưa chúng ta đến một định lý quan trọng trong hình học được gọi là Định lý tổng góc tam giác.

Theo Định lý tổng góc tam giác, tổng ba góc trong trong một tam giác luôn bằng 180 °.

Điều này có thể được viết là;

∠a + ∠b + ∠c = 180 °

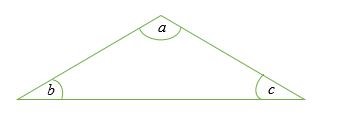
Làm thế nào để tìm các góc trong của một tam giác?

Khi biết hai góc trong của một tam giác, có thể xác định góc thứ ba bằng cách sử dụng Định lý Tổng Góc của Tam giác. Để tìm góc chưa biết thứ ba của tam giác, chỉ cần trừ tổng của hai góc đã biết đi 180 độ.

Hãy xem xét một số vấn đề ví dụ:

ví dụ 1

Tam giác ABC sao cho, ∠A = 38 ° và ∠B = 134 °. Tính ∠C.

Giải pháp

Theo Định lý Tổng góc Tam giác, ta có;

∠A + ∠B + ∠C = 180 °

⇒ 38 ° + 134 ° + ∠Z = 180 °

⇒ 172 ° + ∠C = 180 °

Trừ cả hai bên đi 172 °

⇒ 172 ° – 172 ° + ∠C = 180 ° – 172 °

Do đó, ∠C = 8 °

Ví dụ 2

Tìm các góc thiếu x trong tam giác dưới đây.

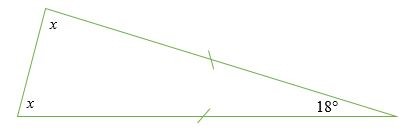
Giải pháp

Theo Định lý Tổng góc Tam giác (Tổng các góc trong = 180 °)

⇒ x + x + 18 ° = 180 °

Đơn giản hóa bằng cách kết hợp các thuật ngữ tương tự.

⇒ 2x + 18 ° = 180 °

Trừ cả hai bên đi 18 °

⇒ 2x + 18 ° – 18 ° = 180 ° – 18 °

⇒ 2x = 162 °

Chia cả hai bên cho 2

⇒ 2x / 2 = 162 ° / 2

x = 81 °

Ví dụ 3

Tìm các góc còn thiếu bên trong hình tam giác dưới đây.

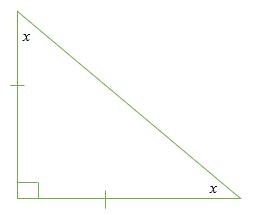
Giải pháp

Đây là một tam giác vuông cân; do đó, một góc là 90 °

⇒ x + x + 90 ° = 180 °

⇒ 2x + 90 ° = 180 °

Trừ cả hai bên đi 90 °

⇒ 2x + 90 ° – 90 ° = 180 ° – 90 °

⇒ 2x = 90 °

⇒ 2x / 2 = 90 ° / 2

x = 45 °

Ví dụ 4

Tìm số đo các góc của tam giác có góc thứ hai hơn góc thứ nhất 15 ° và góc thứ ba hơn góc thứ hai 66 °.

Giải pháp

Để cho;

1 góc ^ST = x °

Góc 2 ^ND = (x + 15) °

3 góc ^RD = (x + 15 + 66) °

Theo định lý tổng góc tam giác,

x ° + (x + 15) ° + (x + 15 + 66) ° = 180 °

Thu thập các điều khoản tương tự.

⇒ 3x + 81 ° = 180 °

⇒ 3x = 180 ° – 81 °

⇒ 3x = 99

x = 33 °

Bây giờ thay x = 33 ° vào ba phương trình.

1 góc ^ST = x ° = 33 °

Góc 2 ^ND = (x + 15) ° = 33 ° + 15 ° = 48 °

3 Góc ^RD = (x + 15 + 66) ° = 33 ° + 15 ° + 66 ° = 81 °

Do đó, ba góc của một tam giác là 33 °, 48 ° và 81 °.

Ví dụ 5

Tìm các góc bên trong bị thiếu của sơ đồ sau.

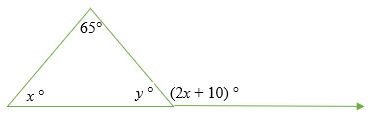
Giải pháp

Góc y ° và (2x + 10) ° là các góc bổ sung (tổng là 180 °)

Vì thế,

⇒ y ° + (2x + 10) ° = 180 °

⇒ y + 2x = 170 ° ……………… (i)

Ngoài ra, theo Định lý Tổng góc Tam giác,

⇒ x + y + 65 ° = 180 °

⇒ x + y = 115 ° ………………… (ii)

Giải hai phương trình đồng thời bằng cách thay thế

⇒ y = 170 ° – 2x

⇒ x + 170 ° – 2x = 115 °

⇒ -x = 115 ° -170 °

x = 55 °

Nhưng, y = 170 ° – 2x

= 170 ° – 2 (55) °

⇒ 170 ° – 110 °

y = 60 °

Do đó, các góc bị thiếu là 60 ° và 55 °

Xem thêm:

Định lý Góc ngoài đơn giản dễ hiểu nhất 2021

Định lý Pitago và những kiến thức cho người mới nhập môn

Ví dụ 6

Tính giá trị của x để tam giác có các góc là; x °, (x + 20) ° và (2x + 40) °.

Giải pháp

Tổng các góc bên trong = 180 °

x ° + (x + 20) ° + (2x + 40) ° = 180 °

Đơn giản hóa.

x + x + 2x + 20 ° + 40 ° = 180 °

4x + 60 ° = 180 °

Trừ 60 cho cả hai bên.

4x + 60 ° – 60 ° = 180 ° – 60 °

4x = 120 °

Bây giờ chia cả hai bên cho 4.

4x / 4 = 120 ° / 4

x = 30 °

Do đó, các góc của tam giác là 30 °, 50 ° và 100 °.

Ví dụ 7

Tìm các góc còn thiếu trong sơ đồ dưới đây.

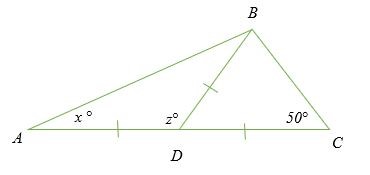
Giải pháp

Tam giác ADB và BDC là các tam giác cân.

∠ DBC = ∠DCB = 50 °

∠ BAD = ∠ DBA = x °

Vì thế,

50 ° + 50 ° + ∠BDC = 180 °

∠BDC = 180 ° – 100 °

∠BDC = 80 °

Nhưng, z ° + 80 ° = 180 ° (Các góc trên một đường thẳng)

Do đó, z = 100 °

Trong tam giác ADB:

z ° + x + x = 180 °

100 ° + 2x = 180 °

2x = 180 ° – 100 °

2x = 80 °

x = 40 °