Định lý trong Toán học là gì?
Các định lý toán học có thể được định nghĩa là các phát biểu được chấp nhận đúng thông qua các phát biểu, phép toán hoặc đối số đã được chấp nhận trước đó. Đối với bất kỳ định lý toán học nào, có một chứng minh được thiết lập để chứng minh tính trung thực của phát biểu định lý.
Tại sao Định lý lại quan trọng trong Toán học?
Có nhiều tầm quan trọng khác nhau của các định lý được coi là chân lý tuyệt đối. Các định lý không chỉ giúp giải quyết các vấn đề toán học một cách dễ dàng mà việc chứng minh chúng còn giúp phát triển sự hiểu biết sâu sắc hơn về các khái niệm cơ bản. Đối với học sinh, các định lý không chỉ là nền tảng của toán học cơ bản mà còn giúp các em phát triển khả năng suy luận khi các em hoàn toàn hiểu được các phát biểu và cách chứng minh của chúng.
Định lý Toán học cho Lớp 10
Trong môn Toán lớp 10, rất nhiều định lý quan trọng được giới thiệu là cơ sở của các khái niệm toán học. Học sinh lớp 10 được yêu cầu phải học kỹ tất cả các định lý với các phát biểu và chứng minh, không chỉ để đạt điểm cao trong kỳ thi hội đồng quản trị mà còn có nền tảng vững chắc hơn trong môn học này. Dưới đây là một số định lý toán quan trọng dành cho lớp 10.
Danh sách các Định lý Toán 10 Quan trọng
Đối với lớp 10, một số định lý quan trọng nhất là:
- Định lý Py-ta-go
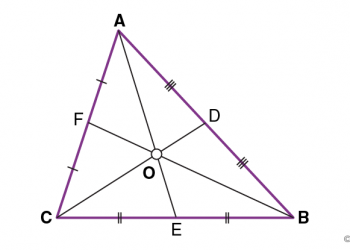
- Định lý điểm giữa
- Định lý còn lại
- Định lý cơ bản của số học
- Định lý góc phân giác
- Định lý góc nội tiếp
- Định lý Ceva
- Định lý Bayes
Ngoài các định lý này, các bài học có các định lý quan trọng nhất là hình tròn và hình tam giác. Dưới đây là một số định lý về tam giác và đường tròn quan trọng đối với tiêu chuẩn thứ 10.
Định lý vòng tròn cho Lớp 10
Có nhiều định lý khác nhau liên quan đến đường tròn. Các định lý về đường tròn rất quan trọng đối với cả học sinh lớp 9 và lớp 10. Một vài định lý quan trọng là:
- Định lý 1: Các hợp âm bằng nhau của một đường tròn phụ các góc bằng nhau tại tâm của đường tròn.
- Ngược lại của Định lý 1: Nếu hai góc phụ tại tâm của hai hợp âm bằng nhau thì các hợp âm đó có độ dài bằng nhau.
- Định lý 2: Đường vuông góc với một hợp âm, chia đôi hợp âm nếu vẽ từ tâm của vòng tròn.
- Ngược lại của Định lý 2: Một đường thẳng đi qua tâm của một đường tròn để phân giác một hợp âm, vuông góc với hợp âm đó.
- Định lý 3: Các dây cung bằng nhau của một đường tròn cách đều tâm của đường tròn (khoảng cách bằng nhau).
- Ngược lại của Định lý 3: Các hợp âm của một đường tròn, ở những khoảng cách bằng nhau từ tâm, có độ dài bằng nhau.
- Định lý 4: Số đo các góc phụ tại một điểm bất kỳ trên chu vi của đường tròn từ cùng một cung bằng một nửa số đo góc ở tâm của cùng một cung.
- Định lý 5: Các góc đối diện trong tứ giác nội tiếp là phụ.
Định lý tam giác cho lớp 10
- Tất cả các số liệu đồng dư là tương tự nhau, nhưng không có nghĩa là tất cả các số liệu tương tự đều đồng dư.
- Hai đa giác có cùng số cạnh bằng nhau nếu các góc tương ứng của chúng bằng nhau và tỷ lệ các cạnh tương ứng của chúng bằng nhau.
- Hai tam giác đồng dạng nếu các góc tương ứng của chúng bằng nhau và các cạnh tương ứng theo cùng một tỷ lệ.
- Trong hai tam giác, nếu các góc tương ứng bằng nhau và các cạnh tương ứng cùng tỉ số thì hai tam giác đó đồng dạng.
- Trong hai tam giác, nếu các cạnh của một tam giác nào đó tỉ lệ với các cạnh của tam giác kia thì các góc tương ứng của chúng bằng nhau và hai tam giác đó đồng dạng.
Bằng chứng
Định lý 1:
Nếu một đường thẳng được vẽ song song với một cạnh của tam giác và cắt hai cạnh kia thì hai cạnh còn lại được chia theo cùng một tỷ lệ.
Cách dựng: ABC là tam giác, DE là đường thẳng song song với BC và cắt AB tại D và AC tại E, tức là DE || BC.
Nối C thành D và B thành E. Vẽ EM ⊥ AB và DN ⊥ AC.


Chúng ta cần chứng minh rằng AD / DB = AE / EC
Bằng chứng:
Diện tích tam giác, ADE = ½ × AD × EM
Tương tự,
Ar (BDE) = ½ × DB × EM
Ar (ADE) = ½ × AE × DN
Ar (DEC) = ½ × EC × DN
Vì thế,
Không khí (ADE) / Ar (BDE) = ½ × AD × EM / ½ × DB × EM = AD / DB
Tương tự,
Ar (ADE) / Ar (DEC) AE / EC
Các tam giác DEC và BDE nằm trên cùng một đáy, tức là DE và nằm giữa hai cạnh DE và BC.
Vì thế,
Ar (BDE) = Ar (DEC)
Từ các phương trình trên, chúng ta có thể nói rằng
AD / DB AE / EC.
Do đó, đã chứng minh.
Định lý 2:
Nếu một đường thẳng chia bất kỳ hai cạnh nào của tam giác theo cùng một tỷ lệ thì đường thẳng đó song song với cạnh thứ ba.
ABC là tam giác trong đó DE chia AC và AB theo cùng một tỉ số. Điều này nói rằng:
AB / DB = AE / EC


Cách dựng: Vẽ đường thẳng DE ‘từ điểm D đến điểm E’ tại AC. Ta xét DE ‘// BC.
Bằng chứng:
Để chứng minh: Nếu DE` || BC, sau đó
AB / DB = AE` / E`C
Theo định lý, AB / DB = AE / EC
Khi đó, E và E` phải trùng nhau.
Điều này chứng tỏ rằng DE || BC
Đã được chứng minh.
Định lý 3:
Trong hai tam giác, nếu các cạnh của một tam giác tỉ lệ với các cạnh của tam giác kia thì các góc tương ứng của chúng bằng nhau và do đó hai tam giác đồng dạng. Nó còn được gọi là tiêu chí SSS (side-side-side).
Hai tam giác ABC và DEF được vẽ sao cho các cạnh tương ứng của chúng tỉ lệ với nhau. Nó có nghĩa là:
AB / DE = AC / DF = BC / EF
Bằng chứng:
Để chứng minh: ∠A = ∠C, ∠B = E và ∠C = ∠F
Do đó, tam giác ABC ~ DEF
Trong tam giác DEF, vẽ đường thẳng PQ sao cho DP = AB và DQ = AC
Vì các cạnh tương ứng của hai tam giác bằng nhau.
Điều này nghĩa là;
DP / PE = DQ / QF = PQ / EF
Điều này cũng có nghĩa là ∠P = ∠E và ∠Q = ∠F
Chúng tôi đã lấy, ∠A = ∠D, ∠B = ∠P và ∠C = ∠Q
Vì thế,
∠A = ∠D, ∠B = ∠E và ∠C = ∠F
Do đó, từ tiêu chí AAA;
Tam giác ABC ~ DEF.
Đã được chứng minh.
Định lý 4:
Định lý Pythagoras: Trong một tam giác vuông, bình phương của cạnh huyền bằng tổng bình phương của hai cạnh còn lại.
Hypotenuse 2 = Cơ số 2 + Vuông góc 2
Bằng chứng:
ABC là tam giác vuông cân tại B. BD vuông góc với cạnh huyền AC vẽ từ đỉnh B.


Để chứng minh: AC 2 = AB 2 + BC 2
Trong tam giác ABC và ADB,
AB / AC AD / AB
AB 2 = AC × AD …………… (1) [Vì đây là các tam giác đồng dạng.]
Trong các tam giác ABC và BDC;
BC / AC = CD / BC
BC 2 = AC × CD …………. (2)
Khi chúng ta thêm 1 và 2, chúng ta nhận được;
AB 2 + BC 2 = AD × AC + CD × AC
AB 2 + BC 2 = AC (AD + CD)
AB 2 + BC 2 = AC 2
Do đó, đã chứng minh.
Đọc thêm:
Hoán vị và kết hợp là gì xem là biết ngay