Cách tìm độ lớn vectơ đơn giản nhất cho bạn

Chúng ta đã biết rằng hai phần của một vectơ là độ lớn của vectơ và hướng của vectơ. Chúng ta có thể học gì về một vectơ từ độ lớn của nó?

Độ lớn của vectơ là độ dài hoặc kích thước của vectơ.

Trong chủ đề này, chúng ta sẽ thảo luận về các khía cạnh sau của độ lớn vectơ:

• Tầm quan trọng của một vectơ là gì?
• Tầm quan trọng của một công thức vectơ
• Làm thế nào để tìm độ lớn của một vectơ?

Tầm quan trọng của một vectơ là gì?

Trong vật lý và toán học, độ lớn của một vectơ có thể được định nghĩa là:

QUẢNG CÁO

“Độ dài của vectơ hoặc khoảng cách giữa điểm đầu và điểm cuối của vectơ.”

Độ lớn của vectơ A được viết dưới dạng | A |. Nếu AB là một vectơ bắt đầu từ điểm A và kết thúc tại điểm B, độ lớn của nó có thể được biểu diễn dưới dạng | AB |.

Nhớ lại rằng vectơ cũng có thể được viết dưới dạng một cặp tọa độ, và chúng ta gọi biểu diễn này là vectơ cột. Ví dụ, vectơ A = (x1, y1) là một vectơ cột. Vectơ này sẽ được mô hình hóa trong hệ tọa độ Descartes dưới dạng một đoạn thẳng kéo dài từ (0,0) đến (x1, y1) với một mũi tên ở cuối, như hình dưới đây. Trong ví dụ này, độ lớn, | A |, của vectơ A là độ dài đoạn thẳng.

Tầm quan trọng của một công thức vectơ

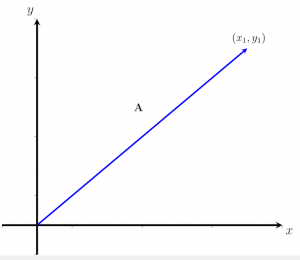
Trong phần này, chúng ta sẽ tìm hiểu các công thức toán học được sử dụng để xác định độ lớn của một vectơ trong các chiều khác nhau.

• Tầm quan trọng của một vectơ trong hai kích thước
• Tầm quan trọng của một vectơ trong ba kích thước
• Tầm quan trọng của một công thức vectơ cho n Thứ nguyên
• Tầm quan trọng của một vectơ sử dụng công thức khoảng cách

Tầm quan trọng của một vectơ trong hai kích thước

Để xác định độ lớn của một vectơ hai chiều từ tọa độ của nó, chúng ta sẽ lấy căn bậc hai của tổng bình phương của mỗi thành phần của nó. Ví dụ, công thức tính độ lớn của vectơ U = (x1, y1) là:

| U | = √x ₁ ^ 2 + y ₁ ^ 2

Công thức này được suy ra từ định lý Pitago.

Tầm quan trọng của một vectơ trong ba kích thước

Để xác định độ lớn của một vectơ ba chiều từ tọa độ của nó, chúng ta sẽ lấy căn bậc hai của tổng bình phương của mỗi thành phần của nó. Công thức về độ lớn của vectơ V = (x1, y1, z1) là:

| V | = √x1 ^ 2 + y1 ^ 2 + z1 ^ 2

Tầm quan trọng của một công thức vectơ cho n Thứ nguyên

Đối với một vectơ n chiều tùy ý, công thức của độ lớn tương tự như công thức được sử dụng trong trường hợp hai và ba chiều.

Cho A = (a1, a2, a3 ……., An) là một vectơ n chiều tùy ý. Độ lớn của nó là:

| A | = √a1 ^ 2 + a2 ^ 2 + a3 ^ 2 +…. + an ^ 2

Vì vậy, bằng cách sử dụng các công thức này, chúng ta có thể dễ dàng xác định độ lớn của bất kỳ vectơ nào trong bất kỳ chiều nào.

Tầm quan trọng của một vectơ sử dụng công thức khoảng cách

Vì độ lớn của vectơ MN  là khoảng cách giữa điểm ban đầu của nó, M và điểm cuối N nên độ lớn của nó được ký hiệu là | MN | Nếu M = (x1, y1) và N = (x2, y2), chúng ta có thể xác định độ lớn của nó bằng công thức khoảng cách như sau:

| MN | = √ (x2-x1) ^ 2 + (y2-y1) ^ 2

Để sử dụng công thức trên, trước tiên chúng ta lấy tọa độ x của điểm cuối và trừ tọa độ x của điểm đầu. Sau đó, chúng tôi bình phương giá trị kết quả. Tương tự, chúng ta trừ tọa độ y của điểm bắt đầu từ tọa độ y của điểm kết thúc và bình phương giá trị kết quả.

Cuối cùng, chúng ta cộng các giá trị bình phương này lại với nhau và lấy căn bậc hai. Điều này sẽ cho chúng ta độ lớn của vectơ.

Xem thêm:

Chi tiết cách tìm một đơn vị Vector chỉ trong giây lát

Góc giữa hai Vectơ – Giải thích và Ví dụ

Làm thế nào để tìm độ lớn của một vectơ?

Trong phần này, chúng ta sẽ thực hành tính toán độ lớn của các vectơ khác nhau.

Ví dụ:

Những ví dụ này bao gồm các giải pháp từng bước để hiểu rõ hơn về cách tính độ lớn vectơ.

ví dụ 1

Biểu thị vectơ AD đã cho như trong hình dưới đây dưới dạng vectơ cột và xác định độ lớn của nó.

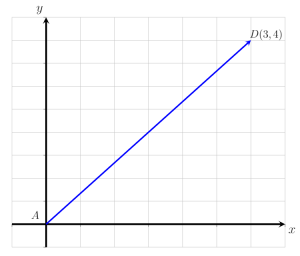
Giải pháp

Theo định nghĩa, một vectơ cột có thể được biểu diễn dưới dạng một cặp có thứ tự. Từ hình trên, có thể thấy vectơ AD bắt đầu tại điểm A và kết thúc tại điểm D. Nó được dịch chuyển 3 điểm sang phải dọc theo trục x và 4 điểm lên trên dọc theo trục y.

Do đó, vectơ AD đã cho có thể được biểu diễn dưới dạng vectơ cột:

AD = (3,4)

Độ lớn của vectơ đã cho có thể được tìm thấy bằng cách sử dụng công thức độ lớn của vectơ hai chiều:

| QUẢNG CÁO | = √ 3 ^ 2 + 4 ^ 2

| QUẢNG CÁO | = √ 9 + 16

| QUẢNG CÁO | = √ 25

| QUẢNG CÁO | = 5

Do đó, độ lớn hay độ dài của vectơ AD là 5 đơn vị.

Ví dụ 2

Biểu thị véc tơ UV đã cho như thể hiện trong hình dưới đây dưới dạng véc tơ cột và xác định độ lớn của nó.

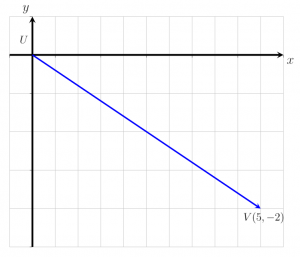
Giải pháp

Theo định nghĩa, một vectơ cột có thể được biểu diễn dưới dạng một cặp có thứ tự. Từ hình trên, có thể thấy rằng vectơ UV bắt đầu tại điểm U và kết thúc tại điểm V. Nó được dịch chuyển 3 điểm sang phải dọc theo trục x và 2 điểm xuống dưới dọc theo trục y.

Do đó, vectơ UV đã cho có thể được biểu thị dưới dạng vectơ cột:

UV = (5, -2)

Lưu ý: -2 chỉ ra rằng vectơ bị dịch chuyển xuống dưới dọc theo trục y.

Độ lớn của vectơ đã cho có thể được tìm thấy bằng cách sử dụng công thức độ lớn của vectơ hai chiều:

| UV | = √ 5 ^ 2 + (-2) ^ 2

| UV | = √ 25 + 4

| UV | = √   29

Do đó, độ lớn hoặc độ dài của vectơ UV là √   29 đơn vị.

Ví dụ 3

Xác định độ lớn của vectơ V = (4, -4, -2).

Giải pháp

Vectơ đã cho là vectơ ba chiều và độ lớn của nó có thể được tính bằng công thức độ lớn ba chiều:

| V | = √ 4 ^ 2 + (-4) ^ 2 + (-2) ^ 2

| V | = √ 16 + 16 + 4

| V | = √ 36

| V | = 6 đơn vị

Như vậy, độ lớn của vectơ ba chiều V là 6 đơn vị.

Ví dụ 4

Xác định độ lớn của vectơ OW, điểm ban đầu là O = (2,5) và điểm cuối cùng là W = (5,2).

Giải pháp

Chúng ta có thể sử dụng công thức khoảng cách để xác định độ lớn của vectơ OW đã cho :

| OW | = √ (5-2) ^ 2 + (2-5) ^ 2

Công thức trên có thể được đơn giản hóa thành:

| OW | = √ (3) ^ 2 + (-3) ^ 2

| OW | = √ 9 + 9

| OW | = √ 18

| OW | = √ 2 * 9

| OW | = √ 2 * (3) ^ 2

| OW | = 3 √ 2 đơn vị

Như vậy, độ lớn của véc tơ OW xấp xỉ 4,242 đơn vị.

Ví dụ 5

Xác định độ lớn của vectơ PQ, điểm ban đầu là P = (-4, 2) và điểm cuối cùng là Q = (3,6).

Giải pháp

Chúng ta có thể sử dụng công thức khoảng cách để xác định độ lớn của vectơ PQ đã cho :

| PQ | = √ (3 – (- 4)) ^ 2 + (6-2) ^ 2

Công thức trên có thể được đơn giản hóa thành:

| PQ | = √ (7) ^ 2 + (4) ^ 2

| PQ | = √ 49 + 16

| PQ | = √ 65 đơn vị

Như vậy, độ lớn của vectơ PQ xấp xỉ 8,062 đơn vị.

Ví dụ 6

Xác định li độ của vectơ AB, điểm ban đầu là A = (3, 2,0) và điểm cuối cùng là B = (0,5, 3).

Giải pháp

Ta có thể sử dụng công thức khoảng cách để xác định độ lớn của vectơ AB đã cho :

| AB | = √ (0-3) ^ 2 + (5-2) ^ 2 + (3-0) ^ 2

Công thức trên được đơn giản hóa thành:

| AB | = √ (-3) ^ 2 + (3) ^ 2 + (3) ^ 2

| AB | = √ 9 + 9 + 9

| AB | = √ 27

| AB | = √ 3 * 9

| AB | = 3 √ 3

Như vậy, độ lớn của vectơ AB xấp xỉ 5.196 đơn vị.

Câu hỏi thực hành

Xác định độ lớn của các vectơ sau:

1. X = 20m, hướng Bắc
2. A = (-1, -2/3)
3. F = (4, 10)
4. V = (2, 5, 3)
5. T = (0, 2, -1)
6. CD = (3, 2, 5)
7. Vectơ OA có điểm đầu là O = (-1,0, 3) và điểm kết thúc là A = (5,2,0)
8. UV, trong đó U = (1, -2) và V = (-2,2)
9. Biểu thị vectơ PQ đã cho trong hình dưới đây dưới dạng vectơ cột và xác định độ lớn của nó.
10. Biểu diễn vectơ MN đã cho như trong hình dưới đây dưới dạng vectơ cột và xác định độ lớn của nó.
11. Tính độ lớn của vectơ XZ trong hình dưới đây với X = (0,1) và Z = (3,6).

Câu trả lời

1. Độ lớn của vectơ đã cho là | X | = 2m.
2. Độ lớn của vectơ A đã cho là | A | = √ 13/9 đơn vị.
3. Độ lớn là | F | = √ 116 đơn vị
4. Độ lớn của vectơ đã cho là | V | = √ 38 đơn vị.
5. Độ lớn của vectơ T là | T | = √ 5 đơn vị.
6. Độ lớn của vectơ đã cho là | CD | = √ 38 đơn vị.
7. Độ lớn là | A | = 7 đơn vị.
8. Độ lớn của vectơ đã cho là | UV | = √ 29 đơn vị.
9. Vectơ PQ có thể được biểu diễn dưới dạng vectơ cột:

PQ = (5,5)

Nghĩa là, vectơ PQ bắt đầu tại điểm P và kết thúc tại điểm Q. Nó được dịch ra 5 điểm sang phải theo trục hoành và 5 điểm lên trên. Độ lớn của vectơ PQ là | PQ | = √ 50 đơn vị.

1. Vectơ MN có thể được biểu diễn dưới dạng vectơ cột:

MN = (-2, -4)

Điều này có nghĩa là vectơ MN bắt đầu tại điểm M và kết thúc tại điểm N. Nó được tịnh tiến 2 điểm sang trái dọc theo trục hoành và 4 điểm xuống dưới dọc theo trục y. Độ lớn của vectơ MN là | MN | = √ 20 đơn vị.

1. Độ lớn của vectơ XZ là | XZ | = √ 45 đơn vị.